Расчеты на прочность при растяжении и сжатии
В результате проведения механических испытаний устанавливают предельные напряжения, при которых происходит нарушение работы или разрушение деталей конструкции. Предельным напряжением при статической нагрузке для пластичных материалов является предел текучести, для хрупких – предел прочности. Для обеспечения прочности деталей необходимо, чтобы возникающие в них в процессе эксплуатации напряжения были меньше предельных. Отношение предельного напряжения к напряжению, возникающему в процессе работы детали, называют коэффициентом запаса прочности и обозначают буквой s:
s =sпред/s, где s= N / A.
Очевидно, что недостаточный коэффициент запаса прочности не обеспечит надежности конструкции, а чрезмерный запас прочности приведет к перерасходу материала и утяжелению конструкции. Сечение, для которого коэффициент запаса прочности наименьший, называется опасным. Минимально необходимый коэффициент запаса прочности называют допускаемым и обозначают [ s ]. Допускаемый коэффициент запаса прочности зависит от свойств, качества и однородности материала, точности представления о нагрузках, действующих на конструкцию, ответственности конструкции и многих других причин. Для пластичных материалов [ s ]=1, 2...2, 5, для хрупких [ s ]=2...5, для древесины [ s ]=8...12. Отношение предельного напряжения к допускаемому коэффициенту запаса прочности называют допускаемым напряжением и обозначают [s]:
[s]=sпред/[ s ].
Условие прочности детали конструкции заключается в том, что наибольшее возникающее в ней напряжение (рабочее) не должно превышать допускаемого: smax< [s].
Условие прочности можно записать в ином виде:
s > [ s ],
т.е. расчетный коэффициент запаса прочности не должен быть меньше допускаемого. Если допускаемые напряжения при растяжении и сжатии различны, то их обозначают соответственно [sр] и [sc]. Расчетная формула при растяжении и сжатии имеет вид
s= N / A < [s]
и читается следующим образом: нормальное напряжение в опасном сечении, вычисленное по формуле s= N / A, не должно превышать допускаемое.
26. Сдвиг (срез)
Сдвигом называется такой вид деформации, при которой в любом поперечном сечении бруса возникает только поперечная сила. Деформацию сдвига можно наблюдать, например, при резке ножницами металлических полос или прутков (рис. 32, а). Рассмотрим брус с площадью поперечного сечения, равной А, перпендикулярно оси которого приложены две равные и противоположно направленные силы F, линии действия их параллельны и находятся на относительно небольшом расстоянии друг от друга (рис. 32, б). Во всех точках поперечного сечения действуют распределенные силы, равнодействующую которых определим из условия равновесия оставленной части бруса:
Рис. 32 S Y =0; F – Q =0,
откуда определим поперечную силу
Q = F.
Поперечная сила (рис. 32, в) есть равнодействующая внутренних касательных сил в поперечном сечении при сдвиге. Естественно считать, что при сдвиге в поперечном сечении бруса действуют только касательные напряжения t. Предполагаем, что эти напряжения распределены по сечению равномерно и, следовательно, их можно вычислить по формуле
t= Q / A.
Очевидно, что при сдвиге форма сечения на значение напряжения не влияет. Расчетная формула на прочность при сдвиге
t= Q / A ≤ [t]
читается следующим образом: касательное напряжение при сдвиге не должно превышать допускаемое. По этой расчетной формуле проводят проектный и проверочный расчеты и определяют допускаемую нагрузку. Наиболее просто однородный чистый сдвиг может быть осуществлен непосредственным нагружением пластины, захваченной в жесткие контурные шарнирно соединенные накладки (рис. 33). Для всех точек пластины касательные напряжения t будут, очевидно, следующими:
где d – толщина пластины. Исключение составляет узкая краевая зона, где пластина сопрягается с накладками. Здесь напряженное состояние будет отличным от чистого сдвига. Однако эти отклонения носят чисто местный характер и область ихраспространения мала по сравнению с общими размерами напряженной пластины.
В качестве еще одного примера иллюстрации состояния однородного чистого сдвига можно рассмотреть тонкостенную цилиндрическую трубку, нагруженную моментами M, приложенными в торцовых плоскостях (рис. 34). Величина напряжения t определяется из условий равенства момента внутренних сил, равномерно распределенных по поперечному сечению, моменту M:
где R – радиус трубки, а d – ее толщина. При сдвиге касательное напряжение t связано с относительной угловой деформацией g соотношением
t=Gg,
называемым законом Гука при сдвиге, где коэффициент пропорциональности G характеризует жесткость материала при сдвиге и называется модулем сдвига или модулем упругости второго рода. Закон Гука при сдвиге справедлив лишь в определенных пределах нагружения и формулируется так: касательное напряжение прямо пропорционально относительному сдвигу. Модуль упругости и напряжение выражаются в одинаковых единицах – Паскалях. Между тремя упругими постоянными E, G и m существует следующая зависимость:
В результате возникающих угловых деформаций пластина, показанная на рис. 33, перекашивается, а торцовые сечения трубки (рис. 34) получают взаимные угловые смещения j. Характер возникающих смещений показан на рис. 35, причем
Рис. 35
Деформация сдвига, доведенная до разрушения материала, называется срезом (применительно к металлическим деталям) или скалыванием (применительно к неметаллическим конструкциям). Допускаемое напряжение на срез выбирают для пластичных материалов в зависимости от предела текучести. В машиностроении для штифтов, болтов, шпонок и т.п. принимают [t]=(0, 25…0, 35)sт.
При расчетах на срез в случае, если соединение осуществляется несколькими одинаковыми деталями (болтами, заклепками и т. д.), полагают, что все они нагружены одинаково. Расчеты соединений на срез обычно сопровождают проверкой прочности этих соединений на смятие.
|

 а
а
 б
б
 в
в
 ,
,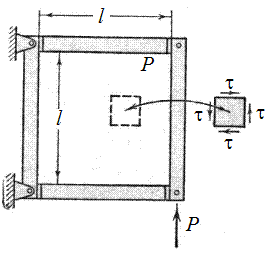 Рис. 33
Рис. 33
 Рис. 34
Рис. 34
 ,
, .
. .
.



