Растяжение и сжатие
Растяжением или сжатием называется такой вид деформации, при котором в любом поперечном сечении бруса возникает только продольная сила. Независимо от условий крепления растянутого или сжатого стержня расчетная схема в рассматриваемых случаях оказывается единой (рис. 21, а – схема растяжения, б – схема сжатия).
Рис. 21
Если изготовить прямой брус из резины (для большей наглядности), нанести на его поверхности сетку продольных и поперечных линий (рис. 22, а) и подвергнуть брус деформации растяжения, то можно отметить следующее: 1) поперечные линии останутся в плоскостях, перпендикулярных оси, а расстояния между ними увеличатся; 2) продольные линии останутся прямыми, а расстояния между ними уменьшатся (рис. 22, б). Если же этот брус подвергнуть деформации сжатия, то: 1) поперечные линии останутся в плоскостях, перпендикулярных оси, а расстояния между ними уменьшатся; 2) продольные линии останутся прямыми, а расстояния между ними увеличатся (рис. 22, в).
Рис. 22
При растяжении и сжатии в поперечных сечениях бруса возникают только нормальные напряжения, равномерно распределенные по сечению и вычисляемые по формуле
s= N / A,
где N – продольная сила; А – площадь поперечного сечения. Очевидно, что при растяжении и сжатии форма сечения на напряжение не влияет. Напряжения и деформации при растяжении и сжатии связаны между собой зависимостью, которая называется законом Гука. Закон Гука при растяжении и сжатии справедлив лишь в определенных пределах нагружения и формулируется так: нормальное напряжение прямо пропорционально относительному удлинению или укорочению. Математически закон Гука можно записать в виде равенства:
s= E e.
Коэффициент пропорциональности Е характеризует жесткость материала, т. е. его способность сопротивляться упругим деформациям растяжения или сжатия, и называется модулем продольной упругости или модулем упругости первого рода. Модуль упругости и напряжение выражаются в одинаковых единицах: [ E ]=[s]/[e]=Па.
Опыт показывает, что в определенных пределах удлинение стержня в продольном направлении сопровождается пропорциональным сужением стержня в поперечном направлении (рис. 23).
eпопер=meпрод,
где m – безразмерный коэффициент пропорциональности, называемый коэффициентом Пуассона. Величина m характеризует упругие свойства материала и определяется экспериментально. Для всех металлов числовые значения m лежат в пределах 0, 25–0, 50.
|



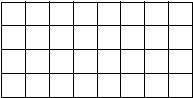
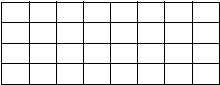

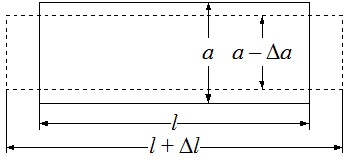 Рис. 23
Рис. 23
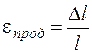 ,
, 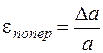 ,
то, как показывает опыт,
,
то, как показывает опыт,



