Теоремы об изменении количества движения точки и механической системы
Количеством движения материальной точки называется векторная величина Единицей измерения количества движения является в СИ – Импульс силы характеризует действие, оказываемое на тело силой за некоторый промежуток времени. Введем понятие об элементарном импульсе, т. е. об импульсе за элементарный промежуток времени d t. Элементарным импульсом силы называется векторная величина
Направлен элементарный импульс вдоль линии действия силы. Импульс
Следовательно, импульс силы за некоторый промежуток времени t 1 равен определенному интегралу от элементарного импульса, взятому в пределах от нуля до t 1. Единицей измерения импульса силы, как и количества движения, является в СИ 1 кг·м/с. Теорема об изменении количества движения точки математически записывается в виде
а формулируется следующим образом: изменение количества движения точки за некоторый промежуток времени равно сумме импульсов всех действующих на точку сил за тот же промежуток времени. Количеством движения системы будем называть векторную величину
Если же движение тела является сложным, то величина Таким образом, количество движения можно рассматривать как характеристику поступательного движения системы (тела), а при сложном движении – как характеристику поступательной части движения вместе с центром масс. Теорема об изменении количества движения системы математически имеет следующий вид:
т.е. изменение количества движения системы за некоторый промежуток времени равно сумме импульсов внешних сил, действующих на систему за тот же промежуток времени.
|

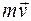 , равная произведению массы точки на ее скорость. Направлен вектор
, равная произведению массы точки на ее скорость. Направлен вектор  , равная произведению силы
, равная произведению силы 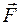 на элементарный промежуток времени d t:
на элементарный промежуток времени d t: .
. любой силы
любой силы  .
. ,
, , равную геометрической сумме (главному вектору) количеств движения всех точек системы (рис. 18) или равную произведению массы всей системы, на скорость ее центра масс:
, равную геометрической сумме (главному вектору) количеств движения всех точек системы (рис. 18) или равную произведению массы всей системы, на скорость ее центра масс:

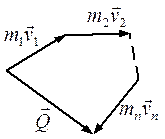
 независимо от того, как вращается колесо вокруг его центра масс С.
независимо от того, как вращается колесо вокруг его центра масс С. ,
,


