Способы задания движения точки. Для задания движения точки можно применять один из следующих трех способов: 1) векторный, 2) координатный
Для задания движения точки можно применять один из следующих трех способов: 1) векторный, 2) координатный, 3) естественный. 1. Векторный способ задания движения точки. Пусть точка М движется по отношению к некоторой системе отсчета Oxyz. Положение этой точки в любой момент времени можно определить, задав ее радиус-вектор При движении точки М вектор
Данное равенство определяет закон движения точки в векторной форме, так как оно позволяет в любой момент времени построить соответствующий вектор Геометрическое место концов вектора Аналитически вектор задается его проекциями на координатные оси. В прямоугольных декартовых координатах для вектора
декартовыми координатами х, у, z, которые при движении точки будут с течением времени изменяться. Чтобы знать закон движения точки, т. е. ее положение в пространстве в любой момент времени, надо знать значения координат точки для каждого момента времени, т. е. знать зависимости x = f 1(t), y = f 2(t), z = f 3(t).
Данные три уравнения представляют собой уравнения движения точки в прямоугольных декартовых координатах. Они определяют закон движения точки при координатном способе задания движения. 3. Естественный способ задания движения точки. Естественным (или траекторным) способом задания движения удобно пользоваться в тех случаях, когда траектория движущейся точки известна заранее. Пусть кривая АВ является траекторией точки М при ее движении относительно системы отсчета Oxyz (рис. 13). Выберем на этой траектории какую-нибудь неподвижную точку О ', которую примем за начало отсчета, и установим на траектории положительное и отрицательное направления отсчета (как на оси координат. Тогда положение точки М на траектории будет однозначно определяться криволинейной координатой s, которая равна расстоянию от точки О ' до точки М, измеренному вдоль дуги траектории и взятому с соответствующим знаком. При движении точка М перемещается в положения M 1, М 2,..., следовательно, расстояние s будет с течением времени изменяться. Чтобы знать положение точки М на траектории в любой момент времени, надо знать зависимость s = f (t), которая выражает закон движения точки М вдоль траектории.
|

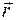 , проведенный из начала координат О в точку М (рис. 12).
, проведенный из начала координат О в точку М (рис. 12). .
. ,
,  ,
,  координатных осей, получим для
координатных осей, получим для  выражение
выражение .
. Рис. 12
Рис. 12
 Рис. 13
Рис. 13



