| Введем важное понятие о моменте силы относительно точки. Точку, относительно которой берется момент, называют центром момента, а момент силы относительно этой точки – моментом относительно центра. Если под действием приложенной силы тело может совершать вращение вокруг некоторой точки, то момент силы относительно этой точки будет характеризовать вращательный эффект силы.
|  Рис. 8
Рис. 8
|
Рассмотрим силу 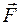 , приложенную к телу в точке A (рис. 8). Из некоторого центра О опустим перпендикуляр на линию действия силы
, приложенную к телу в точке A (рис. 8). Из некоторого центра О опустим перпендикуляр на линию действия силы 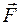 ; длину h этого перпендикуляра называют плечом силы
; длину h этого перпендикуляра называют плечом силы 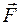 относительно центра О. Момент силы относительно центра О определяется: 1) модулем момента, равным произведению Fh; 2) положением в пространстве плоскости ОАВ («плоскости поворота»), проходящей через центр О и силу
относительно центра О. Момент силы относительно центра О определяется: 1) модулем момента, равным произведению Fh; 2) положением в пространстве плоскости ОАВ («плоскости поворота»), проходящей через центр О и силу 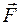 ; 3) направлением поворота в этой плоскости.
; 3) направлением поворота в этой плоскости.
Из геометрии известно, что положение плоскости в пространстве определяется направлением нормали (перпендикуляра) к этой плоскости. Таким образом, момент силы относительно центра характеризуется не только его числовым значением, но и направлением в пространстве, т. е. является величиной векторной.
Введем следующее определение: моментом силы 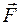 относительно центра О называется приложенный в центре О вектор
относительно центра О называется приложенный в центре О вектор  , модуль которого равен произведению модуля F силы на ее плечо h и который направлен перпендикулярно плоскости, проходящей через центр О и силу, в ту сторону, откуда сила видна стремящейся повернуть тело вокруг центра О против хода часовой стрелки (рис. 8). Согласно этому определению
, модуль которого равен произведению модуля F силы на ее плечо h и который направлен перпендикулярно плоскости, проходящей через центр О и силу, в ту сторону, откуда сила видна стремящейся повернуть тело вокруг центра О против хода часовой стрелки (рис. 8). Согласно этому определению
 .
.
Последний результат следует из того, что площадь треугольника S D AOB = AB · h /2= Fh /2. Измеряется момент силы в ньютон-метрах (H·м).
Найдем формулу, выражающую вектор  . Для этого рассмотрим векторное произведение
. Для этого рассмотрим векторное произведение  векторов
векторов  и
и  . По определению
. По определению
 .
.
Направлен вектор  перпендикулярно плоскости ОАВ в ту сторону, откуда кратчайшее совмещение
перпендикулярно плоскости ОАВ в ту сторону, откуда кратчайшее совмещение  с
с  (если их отложить от одной точки) видно происходящим против хода часовой стрелки, т. е. так же, как вектор
(если их отложить от одной точки) видно происходящим против хода часовой стрелки, т. е. так же, как вектор  . Следовательно, векторы
. Следовательно, векторы  и
и  совпадают и по модулю, и по направлению, и, как легко видеть, по размерности, т. е. выражают одну и ту же величину. Отсюда
совпадают и по модулю, и по направлению, и, как легко видеть, по размерности, т. е. выражают одну и ту же величину. Отсюда
 =
=  или
или 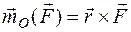 ,
,
где  – радиус-вектор точки A, проведенныйиз центра О.
– радиус-вектор точки A, проведенныйиз центра О.
Таким образом, момент силы F относительно центра О равен векторному произведению радиуса-вектора  , проведенного из центра О в точку А, где приложена сила, на саму силу. Этот результат может служить другим определением понятия о моменте силы относительно центра.
, проведенного из центра О в точку А, где приложена сила, на саму силу. Этот результат может служить другим определением понятия о моменте силы относительно центра.
Отметим следующие свойства момента силы: 1) момент силы относительно центра не изменяется при переносе точки приложения силы вдоль ее линии действия; 2) момент силы относительно центра О равен нулю или когда сила равна нулю, или когда линия действия силы проходит через центр О (плечо равно нулю).

 Рис. 8
Рис. 8
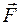 , приложенную к телу в точке A (рис. 8). Из некоторого центра О опустим перпендикуляр на линию действия силы
, приложенную к телу в точке A (рис. 8). Из некоторого центра О опустим перпендикуляр на линию действия силы  , модуль которого равен произведению модуля F силы на ее плечо h и который направлен перпендикулярно плоскости, проходящей через центр О и силу, в ту сторону, откуда сила видна стремящейся повернуть тело вокруг центра О против хода часовой стрелки (рис. 8). Согласно этому определению
, модуль которого равен произведению модуля F силы на ее плечо h и который направлен перпендикулярно плоскости, проходящей через центр О и силу, в ту сторону, откуда сила видна стремящейся повернуть тело вокруг центра О против хода часовой стрелки (рис. 8). Согласно этому определению .
. векторов
векторов  и
и  . По определению
. По определению .
.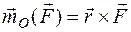 ,
, – радиус-вектор точки A, проведенныйиз центра О.
– радиус-вектор точки A, проведенныйиз центра О. , проведенного из центра О в точку А, где приложена сила, на саму силу. Этот результат может служить другим определением понятия о моменте силы относительно центра.
, проведенного из центра О в точку А, где приложена сила, на саму силу. Этот результат может служить другим определением понятия о моменте силы относительно центра.


