Равновесие системы сходящихся сил
Для равновесия системы сходящихся сил, приложенных к твердому телу, необходимо и достаточно, чтобы равнодействующая, а следовательно, и главный вектор этих сил (см. п. 4) были равны нулю. Условия, которым при этом должны удовлетворять сами силы, можно выразить в геометрической или в аналитической форме. 1. Геометрическое условие равновесия. Так как главный вектор Следовательно, для равновесия системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник, построенный из этих сил, был замкнутым. 2. Аналитические условия равновесия. Аналитически модуль главного вектора системы сил определяется формулой
Так как под корнем стоит сумма положительных слагаемых, то S Fkx =0, S Fky =0, S Fkz =0.
Данные три равенства выражают условия равновесия в аналитической форме: для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы суммы проекций этих сил на каждую из трех координатных осей были равны нулю. Если все действующие на тело сходящиеся силы лежат в одной плоскости, то они образуют плоскую систему сходящихся сил. В случае плоской системы сходящихся сил получим, очевидно, только два условия равновесия: S Fkx =0, S Fky =0.
|
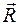системы сил определяется как замыкающая сторона силового многоугольника, построенного из этих сил (см. рис. 6), то 
.
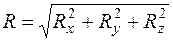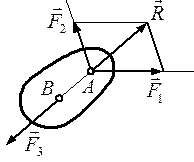Рис. 7
