Парой сил называется система двух равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на абсолютно твердое тело (рис. 9, а). Система сил 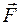 ,
,  , образующих пару, очевидно, не находится в равновесии (эти силы не направлены вдоль одной прямой). В то же время пара сил не имеет равнодействующей, поскольку для любой системы сил равнодействующая равна ее главному вектору
, образующих пару, очевидно, не находится в равновесии (эти силы не направлены вдоль одной прямой). В то же время пара сил не имеет равнодействующей, поскольку для любой системы сил равнодействующая равна ее главному вектору 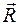 , т. е. сумме этих сил, а для пары
, т. е. сумме этих сил, а для пары 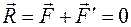 . Поэтому свойства пары сил, как особой
. Поэтому свойства пары сил, как особой
| меры механического взаимо-действия тел, должны быть рассмотрены отдельно.
Плоскость, проходящая через линии действия пары сил, называется плоскостью действия пары. Расстояние d между линиями действия сил пары называется плечом пары. Действие пары сил на твердое тело сводится к некоторому
| 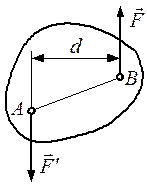
| 
|
| а
| б
|
| Рис. 9
|
вращательному эффекту, который характеризуется величиной, называемой моментом пары. Этот момент определяется: 1) его модулем, равным произведению Fd; 2) положением в пространстве плоскости действия пары; 3) направлением поворота пары в этой плоскости. Таким образом, как и момент силы относительно центра, это величина векторная.
Введем следующее определение: моментом пары сил называется вектор 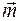 (или
(или  ), модуль которого равен произведению модуля одной из сил пары на ее плечо и который направлен перпендикулярно плоскости действия пары в ту сторону, откуда пара видна стремящейся повернуть тело против хода часовой стрелки(рис. 9, б).
), модуль которого равен произведению модуля одной из сил пары на ее плечо и который направлен перпендикулярно плоскости действия пары в ту сторону, откуда пара видна стремящейся повернуть тело против хода часовой стрелки(рис. 9, б).
Заметим еще, что так как плечо силы 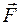 относительно точки А равно d, a плоскость, проходящая через точку А и силу
относительно точки А равно d, a плоскость, проходящая через точку А и силу 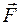 , совпадает с плоскостью действия пары, то одновременно
, совпадает с плоскостью действия пары, то одновременно 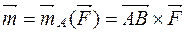 . Но в отличие от момента силы вектор
. Но в отличие от момента силы вектор 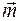 может быть приложен в любой точке (такой вектор называется свободным). Измеряется момент пары, как и момент силы, в ньютон-метрах.
может быть приложен в любой точке (такой вектор называется свободным). Измеряется момент пары, как и момент силы, в ньютон-метрах.
Если принять, что действие пары сил на твердое тело (ее вращательный эффект) полностью определяется значением суммы моментов сил пары относительно любого центра О, то две пары сил, имеющие одинаковые моменты, эквивалентны, т.е. оказывают на тело одинаковое механическое действие. Иначе это означает, что две пары сил, независимо от того, где каждая из них расположена в данной плоскости (или в параллельных плоскостях) и чему равны в отдельности модули их сил и их плечи, если их моменты имеют одно и то же значение 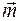 , будут эквивалентны. Так как выбор центра О произволен, то вектор
, будут эквивалентны. Так как выбор центра О произволен, то вектор 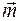 можно считать приложенным в любой точке, т. е. этот вектор свободный.
можно считать приложенным в любой точке, т. е. этот вектор свободный.

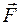 ,
,  , образующих пару, очевидно, не находится в равновесии (эти силы не направлены вдоль одной прямой). В то же время пара сил не имеет равнодействующей, поскольку для любой системы сил равнодействующая равна ее главному вектору
, образующих пару, очевидно, не находится в равновесии (эти силы не направлены вдоль одной прямой). В то же время пара сил не имеет равнодействующей, поскольку для любой системы сил равнодействующая равна ее главному вектору 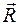 , т. е. сумме этих сил, а для пары
, т. е. сумме этих сил, а для пары 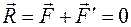 . Поэтому свойства пары сил, как особой
. Поэтому свойства пары сил, как особой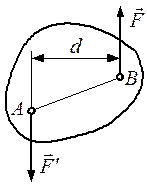

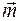 (или
(или  ), модуль которого равен произведению модуля одной из сил пары на ее плечо и который направлен перпендикулярно плоскости действия пары в ту сторону, откуда пара видна стремящейся повернуть тело против хода часовой стрелки(рис. 9, б).
), модуль которого равен произведению модуля одной из сил пары на ее плечо и который направлен перпендикулярно плоскости действия пары в ту сторону, откуда пара видна стремящейся повернуть тело против хода часовой стрелки(рис. 9, б).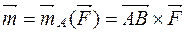 . Но в отличие от момента силы вектор
. Но в отличие от момента силы вектор 


