Приведение плоской системы сил к простейшему виду
Плоская система сил тоже приводится к силе, равной
при этом вектор
Rx =S Fkx, Ry =S Fky,
где все моменты в последнем равенстве алгебраические и сумма тоже алгебраическая. Найдем, к какому простейшему виду может приводиться данная плоская система сил, не находящаяся в равновесии. Результат зависит от значений R и МO. 1. Если для данной системы сил R =0, a MO ≠ 0, то она приводится к одной паре с моментом МO, значение которогоне зависит от выбора центра О. 2. Если для данной системы сил R ≠ 0, то она приводится к одной силе, т. е. к равнодействующей. При этом возможны два случая: а) R ≠ 0, МO =0. В этом случае система, что сразу видно, приводится к равнодействующей R, проходящей через центр О; б) R ≠ 0, МO ≠ 0. В этом случае пару с моментом МO можно изобразить двумя силами R ' и R ", беря R '= R, a R " = – R (рис. 10, б ). При этом, если d = OC – плечо пары, то должно быть
Rd =| MO |.
Отбросив теперь силы R и R ", как уравновешенные, найдем, что вся система сил заменяется равнодействующей R '= R, проходящей через точку С. Положение точки С определяется двумя условиями: 1) расстояние OC = d (
|
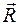и приложенной в произвольно выбранном центре О, и паре с моментом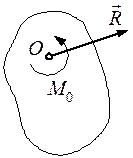
; 
,
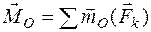
) должно удовлетворять равенству Rd =| MO |; 2) знак момента относительно центра О силы R ', приложенной в точке С, т. е. знак mO (R ') должен совпадать со знаком МO.
