Геометрический способ сложения сил. Равнодействующая сходящихся сил
Решение многих задач механики связано с известной из векторной алгебры операцией сложения векторов и, в частности, сил. Величину, равную геометрической сумме сил какой-нибудь системы, будем в дальнейшем называть главным вектором этой системы сил. Понятие о геометрической сумме сил не следует смешивать с понятием о равнодействующей; для многих систем сил равнодействующей вообще не существует, геометрическую же сумму (главный вектор) можно вычислить для любой системы сил. 1. Сложение двух сил. Геометрическая сумма F двух сил F 1 и F 2 находится по правилу параллелограмма (рис. 4, а) или построением силового треугольника (рис. 4, б), изображающего одну из половин этого параллелограмма. Если угол между силами равен a, то модуль R и углы b, g, которые сила R образует со слагаемыми силами, определяются по формулам:
F 1/sing= F 2/sinb= R /sina.
2. Сложение трех сил, не лежащих в одной плоскости. Геометрическая сумма R трех сил F 1, F 2, F 3, не лежащих в одной плоскости, изображается диагональю параллелепипеда, построенного на этих силах (правило параллелепипеда). В справедливости этого убеждаемся, применяя последовательно правило параллелограмма (рис. 5).
3. Сложение системы сил. Геометрическая сумма (главный вектор) любой системы сил определяется или последовательным сложением сил системы по правилу параллелограмма, или построением силового многоугольника. Второй способ является более простым и удобным. Для нахождения этим способом суммы сил
конец последнего вектора, получаем вектор
4. Равнодействующая сходящихся сил. Рассмотрим систему сходящихся сил, т.е. сил, линии действия которых пересекаются в одной точке (рис. 6, а). Так как сила, действующая на абсолютно твердое тело, является вектором скользящим, то система сходящихся сил эквивалентна системе сил, приложенных в одной точке (на рис. 6, а в точке A). Система сходящихся сил имеет равнодействующую, равную геометрической сумме (главному вектору) этих сил и приложенную в точке пересечения их линий действия. Следовательно система сил
|

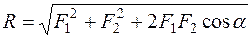 ;
;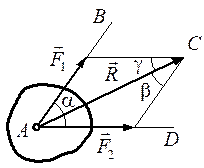
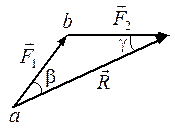

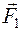 ,
,  ,
, 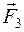 ,...,
,..., 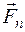 , (рис. 6, а) от произвольной точки О (рис. 6, б) откладываем вектор
, (рис. 6, а) от произвольной точки О (рис. 6, б) откладываем вектор 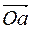 , изображающий в выбранном масштабе силу
, изображающий в выбранном масштабе силу , изображающий силу
, изображающий силу 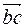 , изображающий силу
, изображающий силу  , изображающий силу
, изображающий силу 
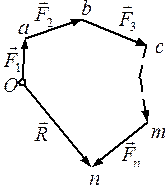
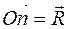 , изображающий главный вектор (геометрическую сумму) слагаемых сил:
, изображающий главный вектор (геометрическую сумму) слагаемых сил: или
или 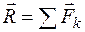 .
.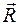 и приложенную в точке А (или в любой другой точке, лежащей на линии действия силы
и приложенную в точке А (или в любой другой точке, лежащей на линии действия силы 


