Теоремы об изменении момента количества движения точки и механической системы (теорема моментов)
В некоторых задачах в качестве динамической характеристики движения точки вместо самого вектора количества движения Эти моменты определяются так же, как и моменты силы:
где При этом вектор Момент количества движения точки относительно какой-нибудь оси Оz, проходящей через центр О, будет равен проекции вектора
где g – угол между вектором
неподвижного центра, равна моменту действующей на точку силы относительно того же центра. Если спроектировать обе части последнего равенства на какую-нибудь ось Оz, проходящую через центр О, получим теорему моментов относительно оси:
Главным моментом количеств движения (или кинетическим моментом) системы относительно данного центра О называется величина
Главный момент количеств движения (кинетический момент) системы может рассматриваться как характеристика ее вращательного движения. Кинетический момент вращающегося тела относительно оси вращения равен произведению момента инерции тела относительно этой оси на угловую скорость тела: Kz = Jz w.
Если система состоит из нескольких тел, вращающихся вокруг одной и той же оси, то Kz = J 1 z w1+ J 2 z w2+…+ Jnz w n.
Теорема моментов для системы математически записывается следующим образом:
т.е. производная по времени от главного момента количеств движения системы, относительно некоторого неподвижного центра равна сумме моментов всех внешних сил системы относительно того же центра.
|

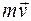 рассматривают его момент относительно некоторого центра или оси.
рассматривают его момент относительно некоторого центра или оси.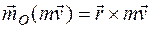 ,
,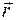 – радиус-вектор движущейся точки, проведенный из центра О.
– радиус-вектор движущейся точки, проведенный из центра О.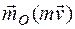 направлен перпендикулярно плоскости, проходящей через mv и центр О, a
направлен перпендикулярно плоскости, проходящей через mv и центр О, a 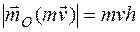 (рис. 19); для сравнения на нем показан и вектор
(рис. 19); для сравнения на нем показан и вектор 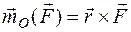 .
.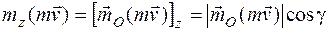 ,
,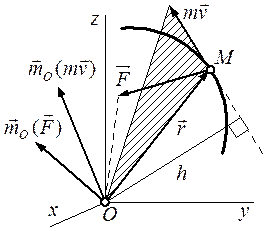 Рис. 19
Рис. 19
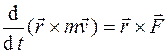 или
или 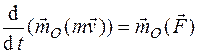 ,
т.е. производная по времени от момента количества движения точки, взятого относительно какого-нибудь
,
т.е. производная по времени от момента количества движения точки, взятого относительно какого-нибудь
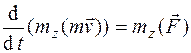 .
.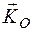 , равная геометрической сумме моментов количеств движения всех точек системы относительно этого центра:
, равная геометрической сумме моментов количеств движения всех точек системы относительно этого центра: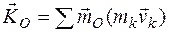 .
.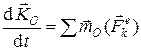 ,
,


