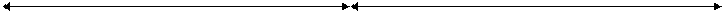Определение опорных реакций. ∑ mСлев = 0 → НA*f - RA*lа + ∑Fi*(lA – а*i) = НA* f – МСб = 0 → НA= МСб / f∑ mB = 0 → RA*l - ∑ Fi*вi = 0 → RA = … ∑ mА = 0 → RВ*l - ∑ Fi*аi = 0 → RВ = … ∑ mСлев = 0 → НA*f - RA*lа + ∑ Fi*(lA – а*i) = НA* f – МСб = 0 → НA= МСб / f
НA= НВ= Н = МСб / f
Mарк= Мкб - Нук Qарк= Qбкcosθ - Hsinθ Nарк= - [ Qбкsinθ + Hcosθ ] Пример 1 расчёта арки на неподвижную нагрузку
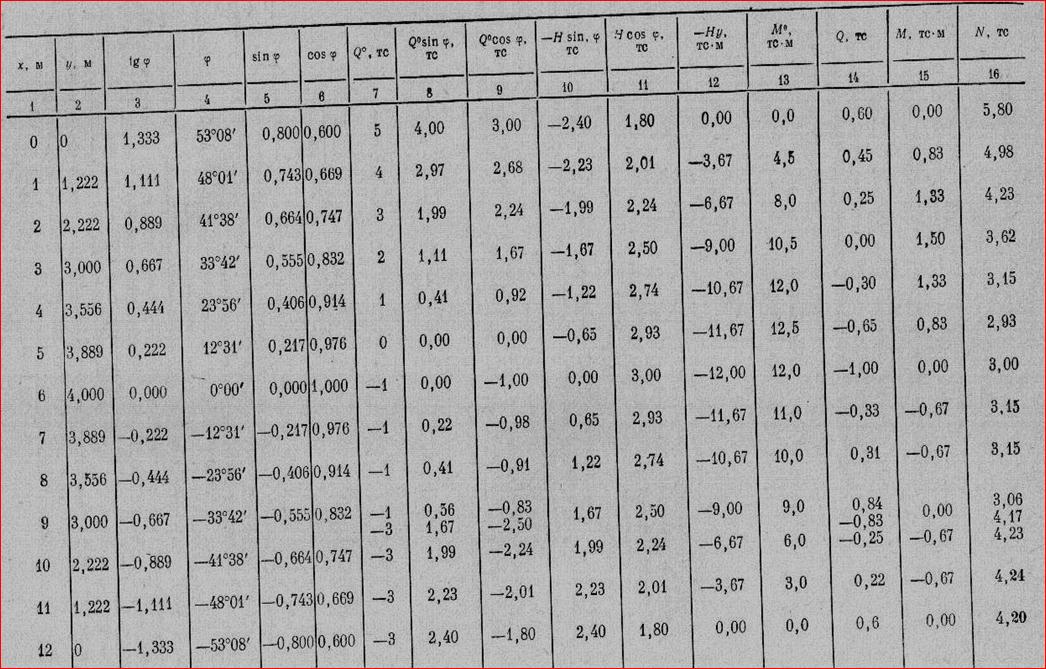
Табличная форма расчёта арки на неподвижную нагрузку
Пример 2 расчёта арки на неподвижную нагрузку
Теорема: Пропорциональность вертикальных ординат у всех точек оси арки, отсчитываемых от опорной прямой АВ, соответствующим ординатам «балочной» эпюры Мб является необходимым и достаточным условием того, чтобы в трёхшарнирной арке при действии заданной вертикальной нагрузке изгибающий момент во всех сечения был равен нулю Пусть ук= k*Мкб, тогда Mарк= Мкб- Н*ук= Мкб- Н*k*Мкб= Мкб (1 – Н*k) так как Мкб= МСб ≠ 0, следовательно (1 – Н*k) = 0 при произвольном k = const
у f
ql/2 lа lв ql/2
L
Пусть ук=4 fх(l -х)/ l2 . Распор Н= МСб / f =q l2 /(8 f). Тогда Mарк= Мкб- Н*ук=…=0
|
∑ mСпр = 0 → НВ*f - RВ*l + ∑ Fi*(lВ – в*i) = НA* f – МСб = 0 → НВ= МСб / f
Определение усилий в арке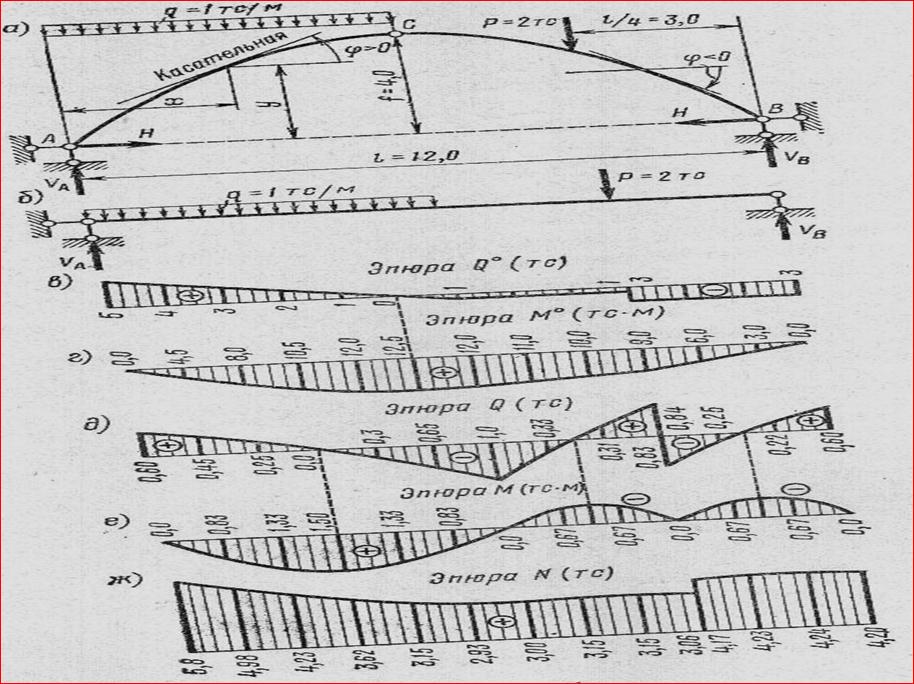
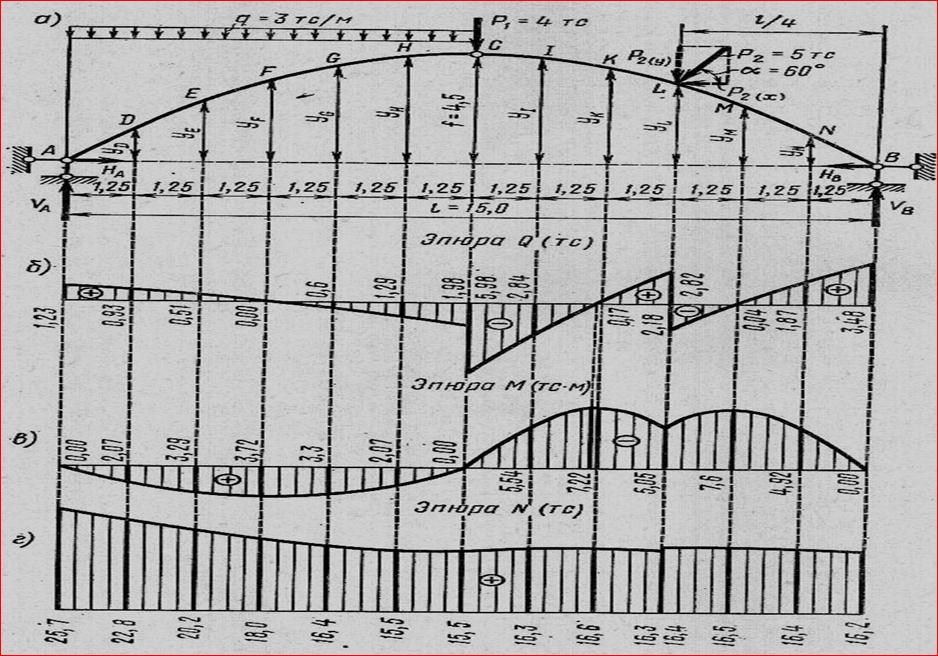
Рациональное очертание оси ТША
q
А В
х
