Выбор рациональной основной системы

 

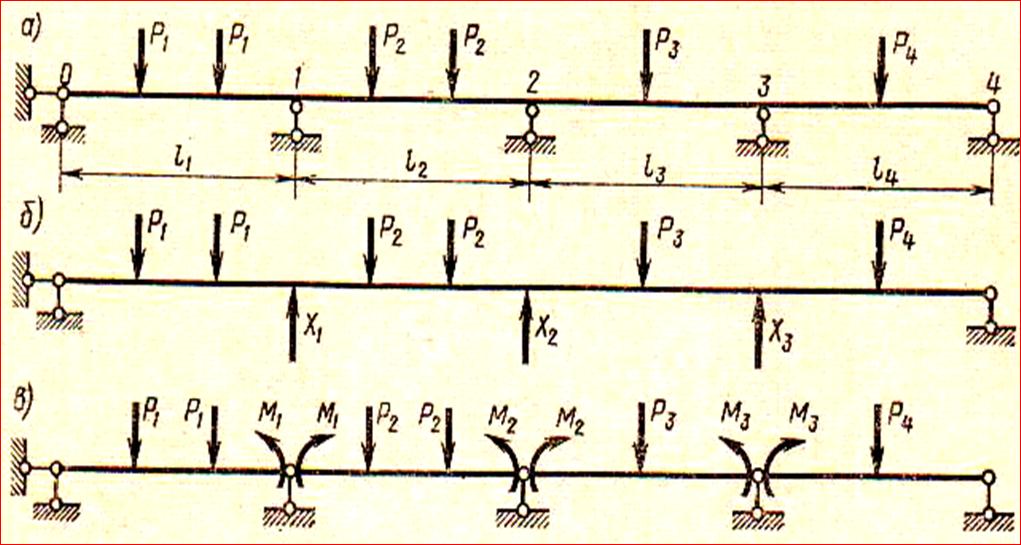
Δ _{i, F} = 0 → δ _{i, 1} X₁ + δ _{i, 2} X₂ + ………. + δ _{i, i} ·X_i + ………… + δ _{i, n} ·X_n +Δ _{i, F} = 0

Δ _{i, F} = 0 → 0 + … + 0 +δ _{i, i-1} М_i-1+ δ _{i, i} ·М_i + δ _{i, i+1}·М_i+1 + 0 + … + 0 +Δ _{i, F} = 0

4. УРАВНЕНИЕ ТРЁХ МОМЕНТОВ ДЛЯ НЕРАЗРЕЗНОЙ БАЛКИ

(учёт внешней нагрузки)

 

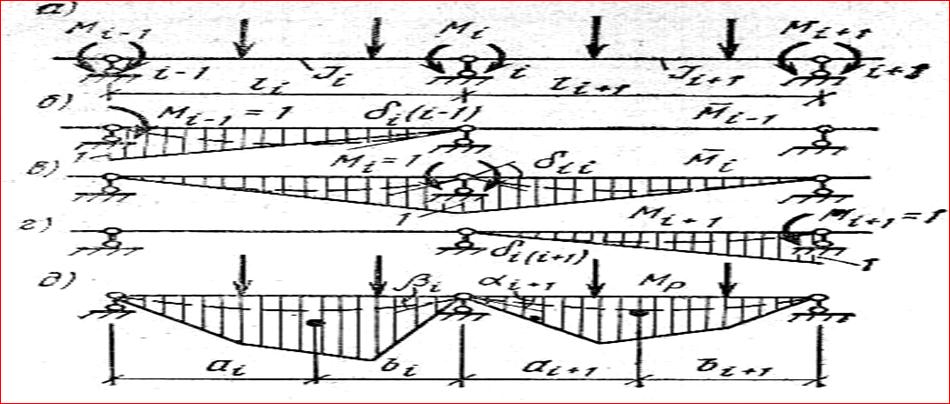
δ _{i, i -1}·М_i-1+ δ _{i, i} ·М_i + δ _{i, i +1}·М_i+1 +Δ _{i , F} = 0

δ _{i, i -1} = (½ ·1· l_i)·(⅓ ·1)/ EJ _i = l_i /(6·EJ _i)

δ _{i, i} = (½ ·1· l_i)·(⅔ ·1)/EJ _i + (½ ·1· l _{i +1})·(⅔ ·1)/EJ _{i +1}=2· l _i/(6·EJ _i) +2· l_{i +1}/(6·EJ _{i +1})

δ _{i, i +1}= (½ ·1· l _{i +1})·(⅓ ·1)/ EJ _{i +1}= l_{i +1}/(6·EJ _{i +1})

Δ _{i , F} = (ω _i · a_i)/(l_i ·EJ _i) +(ω _{i +1}· b_{i +1})/(l_{i +1}·EJ _{i +1})

δ _{i, i -1}·М_i-1+ δ _{i, i} ·М_i + δ _{i, i +1}·М_i+1 +Δ _{i , F} = 0

[ l_i /(6·EJ _i)]·М_i-1+ 2·[ l _i/(6·EJ _i) + l_{i +1}/(6·EJ _{i +1})]·М_i + [ l_{i +1}/(6·EJ _{i +1})]·М_i+1 +

+ (ω _i · a_i)/(l_i ·EJ _i) +(ω _{i +1}· b_{i +1})/(l_{i +1}·EJ _{i +1}) = 0

1) Умножим уравнение на 6·EJ₀;

2) Обозначим λ _i = l _i·EJ₀/EJ_i, где λ _i – приведенная (условная) длина пролёта;

3) Перебросим свободные члены в правую часть …

λ _i ·М_i-1+2·(λ _i +λ _{i +1})·М _i +λ _{i +1}·М _{i +1} = -6 ·ЕJ₀·[(ω _i · a_i)/(l_i ·EJ _i) +(ω _{i +1}· b_{i +1})/(l_{i +1}·EJ _{i +1})]

 

5. Ч а с т н ы е с л у ч а и уравнения трёх моментов

1. При: EJ _i = EJ₀ = const → l _i·М _{i -1}+2·(l_i + l_{i +1})·М _i + l_{i +1}·М _{i +1} = -6·(а _i ·ω _i / l_i +b _{i +1}·ω _{i +1}/ l_{i +1})

2. При: EJ _i = EJ₀ = const; l _i = l = const → М _{i -1}+4·М _i + М _{i +1} = -6·(а _i ·ω _i +b _{i +1}·ω _{i +1})/ l ²

Ч а с т н ы е с л у ч а и уравнения трёх моментов для опор

Левая опора – шарнирная: i=1 → 0 + 2·(λ ₁+λ ₂)·М₁ + λ ₂·М₂ = -6·ЕJ₀·[а₁·ω ₁/(l ₁·ЕJ₁)+b₂·ω _i+1/(l ₂·ЕJ₂)]

Правая опора – шарнирная: i=n → λ _n·М_n-1+2·(λ _n+λ _n+1)·М_n + 0 = -6·ЕJ₀·[а_n·ω _n/(l _n·ЕJ_n)+b_n+1·ω _n+1/(l _n+1·ЕJ_n+1)]

6. Ч а с т н ы е с л у ч а и – наличие консолей

А) Левая консоль:

M₀=- F· l ₀ M₁

F 0 1

l ₀ l ₁

i = 1 → λ ₁М₀ +2·(λ ₁+λ ₂)· М₁ + λ ₂·М₂ = λ ₁(- F· l ₀) +2·(λ ₁+λ ₂)·М₁ + λ ₂·М₂ = ……

б) Правая консоль:

M_nM_n+1 = - m

n n+1 m

l _n+1 l _n+2

i = n → λ _n ·М_n-1+2·(λ _n+λ _n+1)·М_n +λ _n+2·М_n = λ _n ·М_n-1+2·(λ _n+λ _n+1)·М_n +λ _n+2·(- m) = ….

7. Пример 1 расчёта неразрезной балки методом сил

λ _i·М_i-1 + 2·(λ _i+λ _i+1)·М_i + λ _i+1·М_i+1 =-6·ЕJ₀·[а_i·ω _i/(l _i·ЕJ_i)+b_i+1·ω _i+1/(l _i+1·ЕJ_i+1)]

ЕJ_i = ЕJ₀ = ЕJ; λ ₁ = l ₁ = 4, 5 м; λ ₂ = l ₂ =6 м; λ ₃= l ₃=6 м

Левая опора – шарнирная: i=1 → 2·(λ ₁+λ ₂)·М₁ + λ ₂·М₂ = -6· [а₁·ω ₁/ l ₁ +b₂·ω ₂/ l ₂] = -6· [А₁ +В₂]

2(4, 5+6) ·М₁ + 6·М₂ = -6·(6, 07 + 17, 8) 21·М₁ + 6·М₂ = - 143, 22

Правая опора – шарнирная: i=2 → λ ₂ ·М₁+2·(λ ₂+λ ₃)·М₂ = -6·[а₂·ω ₂/ l ₂+b₃·ω ₃/ l ₃] = -6· [А₂ +В₃]

6·М₁ + (6+6)·М₂ = -6·(18, 8 + 13, 8) 6·М₁ + 12·М₂ = -195, 6

Решая СЛУ, получаем: М₁= -4, 89 т·м; М₂ = - 6, 93 т·м

Сводная графическая часть расчётно-проектировочной работы

 

Пример 2 расчёта неразрезной балки методом сил