Структурные формулы кинематических цепей и механизмов

Структурными формулами называются закономерности, связывающие число степеней свободы Н кинематической цепи механизма с числом звеньев и числом и видом его кинематических пар. Если принять что число степеней свободы совпадает с числом обобщенных координат, то для определения H достаточно найти общее число координат определяющих положение всех звеньев и число уравнений связывающих эти координаты. Разность между этими числами дает число независимых координат, если все уравнения связи независимы. Если такие звенья k, то общее число степеней подвижности равно 6k. Соединение звеньев в кинематической цепи определяет связи на движение звеньев. Ограничения движение зависит от класса кинематической пары. Если число пар каждого класса обозначить как P_n, где n – номер класса, то в самом общем случае кинематической цепи будет: P₁ – первого класса, P₂ – второго класса и т.п. Следовательно из 6k степеней подвижности, которые есть у свободных звеньев следует исключить те степени подвижности, которые ограничиваются кинематическими парами. Тогда число степеней подвижности пространственной кинематической цепи будет равно:

H=6k-5p₅-4p₄-3p₃-2p₂-p₁ (1)

Если одно из звеньев кинематической цепи не подвижно (стойка), то степень подвижности кинематической цепи (число степеней подвижности относительно звена, принятого за неподвижное, и

W=6n-5p₅-4p₄-3p₃-2p₂-p₁(2)

Если звенья механизма движутся в одной плоскости, то механизм называется плоским и структурная формула для общего вида таких механизмов принимает вид в виде уравнения «3»

W=3n-2p₅-p₄ (3)

Формула была предложена Чебышевым в 1869 году. Формулы (2) и (3) получены из предложения что все уравнения связи независимы, но это условие выполняется не всегда. В общее число наложенных связей может войти qизбыточных (повторных) связей, которые не уменьшают количество подвижности механизма, обращая его в статически-неопределимую систему. И тогда формула принимает вид:

W=6n-5p₅-4p₄-3p₃-2p₂-p₁+q (4)

W=3n-2p₅-p₄+q (5)

При q=0 механизм представляет статически-определимую систему, и сборка его происходит без деформации звеньев (самоустанавливающийся механизм). Сборка и движение такого механизма происходят при деформации его звеньев. В реальном механизме между элементами кинематических пар имеются зазоры. При движении механизма его звенья могут деформироваться – это причина шума при работе механизма. Поэтому при проектировании:

1. Закладывают точность изготовления деталей и монтажа деталей.

2. При проектировании предусматривают жесткость корпусных деталей для исключения перекоса осей вращения кинематических пар и параллельного смещения осей, шарниров или направляющих. Иначе возможно защемление или интенсивного изнашивания.

Все механизмы, в том числе и плоские, при анализе и синтеза структуры должны рассматриваться как пространственные.

 

 

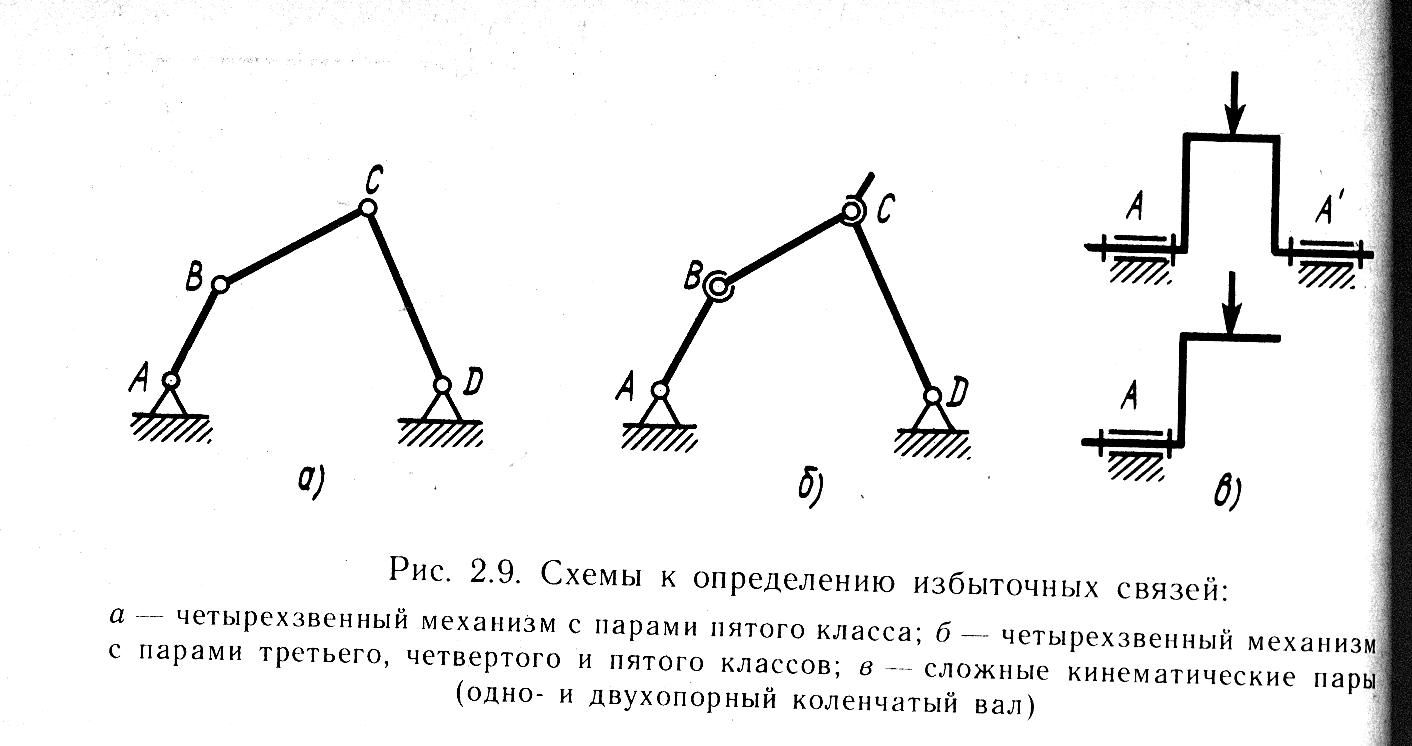
В плоском четырехзвенном механизме (рис 2.9 А)

Все кинематические пары 5 класса являются одноподвижные. Если оси шарниров A, B, C, Dстрого параллельны между собой, то по формуле (3) степень подвижности. Степень подвижности будет равна:

W=3n-2p₅=3x3-2x4=1-6x3+5x4=3

Если точный механизм рассматривать как пространственный, то при W=1 число избыточных связей будет:

Q=W-6n+5p5=1-6x3+5x4

Устраняют их изменение подвижности отдельных кинематических пар. Если шарнир B заменить кинематической парой 3 класса, а шарнир Cзаменить сферической парой с пальцем (4 класс), то избыточные связи в механизме будут отсутствовать и W=1.

 

Рис 2.11

Рисунок 2.11 иллюстрирует замену высшей кинематической пары плоских механизмов звеном входящем в 2 низшие кинематические пары 5 класса. Механизм с низкими кинематическими парами называется заменяющий.