Краткая теория вопроса и метода измерения
Напомним, что механика твердого тела основана на использовании абстрактной модели – понятии «абсолютно твердого тела». Абсолютно твердым телом называется тело, которое ни при каких условиях не может деформироваться, т.е. при любых условиях расстояние между какими-либо двумя его точками (или частицами тела) остается постоянным. В природе абсолютно твердых тел нет, т.е. это – идеализированная модель. Деформацией твердого тела (объекта природы) называется изменение его размеров и объема, сопровождающееся чаще всего изменением формы этого тела. Лишь в случаях всестороннего равномерно распределенного по поверхности тела сжатия или растяжения форма тела не меняется. Причины деформаций: - изменение температуры (тепловое расширение); - внешние силовые воздействия. При деформациях происходят смещения частиц, находящихся в узлах кристаллической решетки, из первоначальных положений в новые, т.е. изменяется взаимное расположение частиц тела. Это приводит к следующему: 1) возникновению упругих сил взаимодействия между частицами (смещенными от положения равновесия), которые стремятся вернуть их в исходные положения; внутренние упругие силы уравновешивают внешние силовые факторы, приложенные к телу; 2) увеличению потенциальной энергии деформируемого тела на величину работы, совершенной при смещении частиц, по преодолению внутренних упругих сил. Различают упругие и пластические (остаточные) деформации. В первом случае тело полностью, а во втором лишь частично, восстанавливает свои прежние размеры и форму после снятия внешней нагрузки. В реальности все деформации в той или иной степени пластичны. Но если остаточные деформации пренебрежимо малы, то можно считать деформацию упругой. Этому отвечают малые деформации. В пределах малых деформаций все деформации удовлетворяют следующим основным законам: - в пределах упругости деформация пропорциональна величине внешнего усилия; - перемена знака внешнего усилия вызывает только перемену знака деформации, без изменения ее абсолютной величины; - при действии нескольких внешних усилий общая деформация равна сумме частных деформаций. В теории упругости доказывается, что все виды деформаций (растяжение или сжатие, сдвиг, изгиб, кручение) могут быть сведены к одновременно происходящим деформациям растяжения (сжатия) и сдвига. Остановимся на одностороннем или продольном растяжении (сжатии), которое состоит в увеличении (уменьшении) длины тела под действием растягивающей (сжимающей) силы F. Для этого рассмотрим однородный стержень (проволоку) длиной l и площадью поперечного сечения S, один конец которого закреплен, а к другому приложена сила F, изменившая длину стержня на величину Мерой деформации служит относительная деформация, которая в данном случае определяется так:
Величины (1) и (2) связаны в случае упругих деформаций по закону Гука:
Коэффициент пропорциональности Е в формуле (3) называется модулем Юнга – характеристика упругих свойств материала, а коэффициент k в (4) – коэффициентом упругости тела. Из (3) следует, что модуль Юнга определяется напряжением, вызывающим удвоение длины стержня. Т.е. модуль Юнга равен напряжению, при котором относительное удлинение стало бы равным единице. Если бы при таком относительном удлинении еще сохранялась пропорциональность между ним и напряжением. В действительности, гораздо раньше, чем будет достигнуто напряжение, равное модулю Юнга, тело начнет испытывать пластическую деформацию, а затем подвергнется разрыву. Деформация твердых тел подчиняется закону Гука лишь до определенного предела, называемого пределом пропорциональности. Продольная деформация стержня всегда вызывает его поперечную деформацию: удлиняясь стержень становится соответственно тоньше. относительная поперечная деформация: Из опыта вытекает взаимосвязь: Далее рассчитаем работу, которую нужно совершить, чтобы растянуть данный стержень на величину Величина
Для проведения измерений выразим модуль Юнга из формулы (3’):
В случае исследования проволоки круглого сечения имеем
Экспериментальная установка схематично изображена на рисунке. Микроскопы первоначально настраиваются на видение каждой из 2-х меток. Нагружение проволоки приводит к их смещению, а разность величин этих смещений дает величину абсолютной деформации соответствующего участка проволоки между метками.
Вопросы к допуску. 1. Какой вид деформации твердого тела будет исследоваться вами в данной работе? 2. Какие величины количественно характеризуют этот вид деформации? 3. Дайте определение и поясните физический смысл модуля Юнга? Эта величина служит характеристикой данного образца, материала из которого он изготовлен или того и другого сразу? 4. В чем существенное отличие модуля Юнга от коэффициента упругости? Могут ли эти величины быть численно равны? Запишите в тетрадь справочные данные о примерах значений величин E и k. 5. Имеет ли смысл говорить о значении модуля Юнга в случае неупругой деформации некоторого тела? 6. Дать определение продольной и поперечной относительных деформаций стержня. Как связаны эти величины? 7. Записать расчетную формулу и пояснить входящие в нее величины и способ их измерения в данной работе. 8. Как в работе определяется цена деления окулярной шкалы? 9. Пояснить величины, стоящие в заголовках столбцов таблицы 1. Имеет ли смысл нахождение среднего значения величины из последнего столбца этой таблицы? Почему? Чему на графике соответствует среднее значение указанной величины? Как оно связано с характером деформации? 10. Каковы возможные источники погрешностей искомого результата? Какие ваши действия по ходу работы могут их уменьшить? 11. Какие переменные в формуле (9) будут браться в качестве отдельных множителей при оценке погрешности косвенного измерения? Каково их количество? Содержание экспериментальных заданий. Задание 1. Определение цены деления шкалы окулярного микрометра 1) Поместить объективный микрометр в поле обзора микроскопа и получить его видимость в окуляре микроскопа. 2) Посчитать число делений объективного микрометра, умещающихся на n делениях шкалы окуляра. Найти количество делений микрометра, приходящихся на одно деление окуляра. 3) Зная цену деления объективного микрометра вычислить цену деления окулярной шкалы микроскопа. Записать полученное значение под таблицей 1. Задание 2. Определение сечения S данной проволоки и длины исследуемого участка 1) Провести 10 измерений микрометром диаметра проволоки в различных местах между установленными метками. 2) Вычислить среднее значение диаметра проволоки 3) Произвести вычисление средней площади поперечного сечения данной проволоки 4) С помощью миллиметровой линейки измерить расстояние 5) Вычислить коэффициент 6) Сохранить полученное исходное состояние проволоки для проведения действий из задания 3. Задание 3. Построение графика растяжения проволоки. 1) Зафиксировать по окулярным шкалам положение меток в исходном состоянии проволоки (см. задание 2). 2) Осторожно нагрузить незакрепленный конец проволоки грузом известной массы 3) Найти с помощью микроскопов соответствующие смещения 4) Вычислить соответствующее растяжение проволоки на данном участке 5) Полученные в пунктах 1)-4) значения указанных величин занести в таблицу 1, проделав аналогичную последовательность для разных по массе нагрузках не менее 7 раз. Таблица 1.
6) Построить на миллиметровой бумаге сглаженный график зависимости 7) Укажите отчетливо точки, соответствующие экспериментально полученным значениям из таблицы 1. 8) Проведите прямую, наиболее близко соответствующую положению отмеченных экспериментальных точек. Найдите угловой коэффициент наклона 9) На основе анализа полученной формы графика сделать вывод о характере деформации проволоки и о возможности применить расчетную формулу. 10) Проделав нужные вычисления заполнить последний столбец таблицы 1. 11) Подумайте, как связана величина Задание 4. Определение значения модуля Юнга материала проволоки. 1) Вычислить по данным эксперимента значение Е на основе расчетной формулы (9), взяв среднее значение 2) Сравните полученное значение с величиной 3) Оценить погрешность результата проделанного измерения как косвенного однократного измерения. Записать ответ в форме 4) Найдите в справочной таблице значение модуля Юнга, близкое к полученному вами значению Е. Какому материалу согласно справочной таблице оно соответствует? 5) Сделайте вывод о соответствии или несоответствии полученного результата материалу, из которого изготовлена исследуемая проволока. Задание 5. Исследование зависимости плотности потенциальной энергии деформации от относительного удлинения. Взяв значение величины Е. полученное в задании 4, и на основе данных из таблицы 1 заполните таблицу 2. При расчете используйте формулу (8). Таблица 2.
2) Постройте график зависимости 3) Охарактеризуйте тип зависимости на основе полученного графика и сделайте пояснения на основе рассмотрения сути происходящих при деформации физических процессов.
Вопросы к отчету:
1. Как проявляются упругие свойства металлов? 2. Какая деформация называется продольной? Что служит ее мерой? 3. Изобразите диаграмму растяжения металлического стержня и укажите на ней точки соответствующие пределу пропорциональности и пределу упругости. В чем сходство и в чем различие этих двух понятий? 4. Что представляет собой величина d в формуле (5) в случае стержня с прямоугольным сечением? 5. Выведите расчетную формулу. Какие допущения были сделаны при этом? 6. Каковы единицы измерения модуля Юнга? 7. Что называется потенциальной энергией? Что принимают на потенциальную энергию упругой деформации? 8. Как экспериментально можно определить модуль Юнга некоторого металла? 9. Каким законам удовлетворяют малые деформации? Чему соответствует условие их «малости»? Как и где в ходе работы применялся закон сложения деформаций?
Лабораторная работа № 1.5. Измерение промежутков времени.
Цель работы: изучить методы измерения промежутков времени; экспериментально определить период вращения мотора стробоскопическим методом. Приборы и принадлежности: метроном, секундомер, электромотор, шестисекторный диск с 2-хцветной окраской секторов, стробоскопическая лампа, ЛАТР.
|

 . Величина силы
. Величина силы 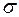 , приходящаяся на единицу площади поперечного сечения стержня, называется напряжением:
, приходящаяся на единицу площади поперечного сечения стержня, называется напряжением:  (1).
(1).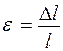 (2) - относительная продольная деформация.
(2) - относительная продольная деформация. (3) или
(3) или  (3’) Þ
(3’) Þ 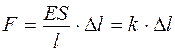 (4).
(4). (5), где
(5), где  - диаметр стержня.
- диаметр стержня. (6), где
(6), где  - положительный коэффициент, зависящий от свойств материала, называемый коэффициентом Пуассона.
- положительный коэффициент, зависящий от свойств материала, называемый коэффициентом Пуассона. . Принимая за ноль значение потенциальной энергии тела в отсутствие деформации, получим выражение для определения потенциальной энергии упруго деформируемого тела:
. Принимая за ноль значение потенциальной энергии тела в отсутствие деформации, получим выражение для определения потенциальной энергии упруго деформируемого тела:  или
или  (7). Где V – объем стержня (изменение объема стержня при его деформации здесь не учитывалось!).
(7). Где V – объем стержня (изменение объема стержня при его деформации здесь не учитывалось!). (8) называется плотностью потенциальной энергии. В случае однородного стержня при одинаковой в любой его точке деформации энергию можно считать равномерно распределенной по объему стержня. В общем случае неоднородной деформации плотность энергии может меняться от точки к точке.
(8) называется плотностью потенциальной энергии. В случае однородного стержня при одинаковой в любой его точке деформации энергию можно считать равномерно распределенной по объему стержня. В общем случае неоднородной деформации плотность энергии может меняться от точки к точке. .
. , тогда расчетная формула для нахождения значения модуля Юнга материала проволоки примет окончательный вид:
, тогда расчетная формула для нахождения значения модуля Юнга материала проволоки примет окончательный вид:  (9).
(9).
 .
. и рассчитать погрешность проделанных многократных прямых измерений.
и рассчитать погрешность проделанных многократных прямых измерений. .
. (10)
(10) .
.
 и
и  каждой метки в делениях окулярной шкалы.
каждой метки в делениях окулярной шкалы. и записать его значение в метрах, зная цену деления окулярной шкалы (см. задание 1).
и записать его значение в метрах, зная цену деления окулярной шкалы (см. задание 1). , Н
, Н
 , дел
, дел
 , дел
, дел

 , отложив по вертикали значения силы, а по горизонтали соответствующие удлинения.
, отложив по вертикали значения силы, а по горизонтали соответствующие удлинения. этой прямой к горизонтальной оси.
этой прямой к горизонтальной оси. . Поясните результат этого сравнения.
. Поясните результат этого сравнения. ,
,  .
.
 , Дж/м3
, Дж/м3
 .
.


