Краткая теория волн
Любая частица упругой среды, выведенная из положения равновесия, под действием упругих сил стремиться возвратиться в первоначальное положение и совершает колебания. Если смещения невелики, упругая сила прямо пропорциональна смещению, и колебания будут совершаться по гармоническому закону: Колебание одной частицы не остается локализованным – начинают колебаться соседние с ней частицы, затем следующие и т.д.; такая совокупность колеблющихся частиц образует волну. Скорость распространения колебаний (волны), зависящая от природы среды, и амплитуда колебаний определяют величину смещения каждой частицы в заданный момент времени. Распределение величин смещений частиц в волне в зависимости от времени и положения частицы описывается уравнением волны, имеющим вид:
Скорость продольных волн, в которых частицы колеблются вдоль направления распространения волны, определяется модулем упругости (коэффициентом пропорциональности между напряжением и относительной деформацией в законе Гука); скорость волн поперечных, в которых частицы колеблются перпендикулярно к направлению распространения волны, - модулем сдвига. Появление звука всегда обусловлено колебаниями какого-либо тела. Распространение звука в газах осуществляется продольными волнами. Уравнение волны (2) соответствует проходящей волне (амплитуда колебаний всех точек волны одинакова, а фаза запаздывает). Если в среде одновременно распространяются 2 волны одинаковой длины, наблюдается сложение этих волн (интерференция). Если направления смещения частиц слагающих волн совпадают, то результирующее смещение равно алгебраической сумме смещений. Тогда результирующее колебание в точке А, отстоящей от первого источника на расстоянии х1, а от второго – на х2, запишется так:
При отражении проходящей волны от границ раздела 2-х сред образуется так называемая стоячая волна (разные точки колеблются с различными амплитудами, но с одинаковыми фазами). Смещение частиц в такой волне определяется по (3) для суммы прямой и обратной волн. Надо только иметь в виду, что в случае отражения от более плотной стенки амплитуда отраженной волны будет Условие возникновения стоячей волны: наложение двух встречных плоских волн с одинаковыми частотой и амплитудой. Т.е. она возникает, например, при отражении волн от преград. Распределение смещений (амплитуд) в стоячей волне при отражении от более плотной среды дается уравнением:
где Также, есть и точки с максимальной амплитудой – пучности. Расстояние между двумя соседними неподвижными точками (узлами), или между соседними пучностями, равно половине длины проходящей волны. Вблизи узлов имеет место максимум деформации, а значит и максимум потенциальной энергии. Вблизи пучностей стоячей волны находятся пучности скорости, а значит максимальна энергия кинетическая. Т.о. дважды за период происходит переход энергии от каждого узла к соседним с ним пучностям и обратно. В случае стоячей волны переноса энергии нет, т.к. падающая и отраженная волны одинаковой амплитуды несут одинаковую энергию в противоположных направлениях. Полная энергия стоячей волны, заключенная между узловыми точками, остается постоянной. Лишь в пределах расстояний, равных
|

 (1), где
(1), где  - величина смещения точки;
- величина смещения точки;  и
и  - амплитуда и начальная фаза колебаний, определяемые начальными условиями (выбором начала отсчета времени можно добиться выполнение
- амплитуда и начальная фаза колебаний, определяемые начальными условиями (выбором начала отсчета времени можно добиться выполнение  ).
).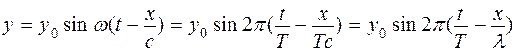 (2), где х – расстояние частицы от начала координат, с – скорость распространения волны, Т – период колебания,
(2), где х – расстояние частицы от начала координат, с – скорость распространения волны, Т – период колебания,  - длина волны. Скорость распространения волн определяется формулой:
- длина волны. Скорость распространения волн определяется формулой: (3), где Е – модуль упругости среды,
(3), где Е – модуль упругости среды,  - ее плотность.
- ее плотность. (3), где
(3), где  , у01 и у02 – амплитуды 2-х слагающих колебаний (начальные фазы их предполагаются совпадающими). Первый множитель в (3) – результирующая амплитуда колебаний в заданной точке. Отсюда видно, что при
, у01 и у02 – амплитуды 2-х слагающих колебаний (начальные фазы их предполагаются совпадающими). Первый множитель в (3) – результирующая амплитуда колебаний в заданной точке. Отсюда видно, что при имеем минимум амплитуды колебаний.
имеем минимум амплитуды колебаний. (т.е. фаза меняется на противоположную или, иначе говоря, идет потеря
(т.е. фаза меняется на противоположную или, иначе говоря, идет потеря  ).
). (4),
(4), - расстояние от точки возникновения волны до места отражения. Переходя от точки к точке вдоль направления волны, будем отмечать различные амплитуды колебаний, определяемые выражением, стоящим перед косинусом в (8). Отсюда следует наличие точек (узлов), для которых эта амплитуда равна нулю:
- расстояние от точки возникновения волны до места отражения. Переходя от точки к точке вдоль направления волны, будем отмечать различные амплитуды колебаний, определяемые выражением, стоящим перед косинусом в (8). Отсюда следует наличие точек (узлов), для которых эта амплитуда равна нулю:  (5).
(5).


