Краткая теория вопроса. Опр.1 Вращательное движение – движение, при котором все точки тела движутся по (коаксиальным) окружностям
Опр.1 Вращательное движение – движение, при котором все точки тела движутся по (коаксиальным) окружностям, центы которых лежат на одной и той же прямой, называемой осью вращения. Для характеристики вращательного движения тела используются параметры, одинаковые для всех точек тела: · Угловое перемещение (угол поворота) · Угловая скорость · Угловое ускорение При описании вращательного движения важнейшими динамическими характеристиками являются момент силы Опр.2 Моментом силы Вектор Когда речь идет о моменте силы относительно оси, то в качестве точки О берется проекция точки приложения силы на эту ось!!! Направление вектора момента силы относительно оси определяется правилом буравчика.
Аналогично, различают момент импульса относительно оси и относительно центра (точки). Момент импульса относительно центра «О» равен Опр.3 Скалярная величина, равная произведению массы материальной точки I=mR2 (1). Момент инерции тела (понимаемого как система материальных точек или частиц) относительно какой-либо оси равен сумме моментов инерции всех материальных точек тела относительно этой оси: Момент инерции тела (понимаемого как сплошная среда) с плотностью Момент инерции тела относительно какой-либо оси является физической величиной, характеризующей инертность тела по отношению к вращению вокруг этой оси.
Основной закон динамики вращательного движения твердого тела вытекает из уравнения моментов и имеет вид:
Здесь Если во время движения I=const, то уравнение (1) примет вид:
Основной закон динамики вращательного движения устанавливает связь между угловым ускорением вращающегося тела, моментом приложенных к нему сил и его моментом инерции. Формулируется закон таким образом: угловое ускорение вращающегося тела пропорционально суммарному моменту всех сил, приложенных к нему, и обратно пропорционально моменту инерции этого тела. Основной закон динамики вращательного движения – это второй закон Ньютона, записанный с использованием величин, характеризующих этот вид механического движения. Его значение – возможность записи уравнений движения любого вращающегося тела.
|

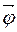 – это угол между радиусами, проведенными из центра окружности, описываемой движущейся точкой, в начальный и конечный моменты времени его движения. Измеряется в радианах.
– это угол между радиусами, проведенными из центра окружности, описываемой движущейся точкой, в начальный и конечный моменты времени его движения. Измеряется в радианах.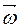 – величина, показывающая изменение угла поворота за единицу времени. Измеряется в радианах в секунду. Направление угловой скорости определяется по правилу правого винта.
– величина, показывающая изменение угла поворота за единицу времени. Измеряется в радианах в секунду. Направление угловой скорости определяется по правилу правого винта.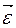 – величина, показывающая изменение угловой скорости за единицу времени. Измеряется в радианах на секунду в квадрате.
– величина, показывающая изменение угловой скорости за единицу времени. Измеряется в радианах на секунду в квадрате.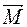 и момент импульса
и момент импульса 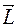 . Момент силы характеризует в динамике ее способность вызывать вращение тел и изменять угловую скорость. Различают момент силы относительно центра (точки) и относительно оси.
. Момент силы характеризует в динамике ее способность вызывать вращение тел и изменять угловую скорость. Различают момент силы относительно центра (точки) и относительно оси.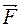 относительно центра «О» называется векторная величина
относительно центра «О» называется векторная величина 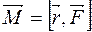 , где
, где 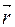 — радиус-вектор точки приложения силы, проведенный из центра.
— радиус-вектор точки приложения силы, проведенный из центра.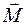 направлен перпендикулярно плоскости, в которой лежат векторы
направлен перпендикулярно плоскости, в которой лежат векторы  и
и  .
. Момент импульса
Момент импульса 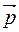 в поступательном движении.
в поступательном движении.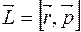 .
.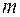 на квадрат ее расстояния от оси вращения, называется моментом инерции материальной точки относительно оси вращения:
на квадрат ее расстояния от оси вращения, называется моментом инерции материальной точки относительно оси вращения: .
. вычисляется интегрированием по его объему:
вычисляется интегрированием по его объему: 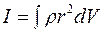 , где dV - элемент объема.
, где dV - элемент объема.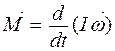 (2), причем
(2), причем 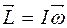 .
. (2’)
(2’)


