Описание метода и установки
Законы вращательного движения проверяются на установке, называемой маятником Обербека (рис. 2). Маятник Обербека представляет собой крестовину (состоит из четырех стержней, закрепленных наглухо крестом под углом 900 друг к другу), вращающуюся вокруг горизонтальной оси. и четырех грузов массой m, которые могут перемещаться вдоль стержней и закрепляться на различных расстояниях (R) от оси вращения. На оси имеется двухступенчатый шкив с радиусами r1 и r2, на который наматывается нить. Выбор радиуса шкива задает
При этом шкив со стержнями и расположенными на них грузами будет вращаться с угловым ускорением
Установим основные физические закономерности, наблюдаемые на маятнике Обербека. При движении груза P на него действуют две силы, определяющие его ускорение: сила тяжести
где mгр. - масса груза, Сила натяжения, приложенная к шкиву по касательной, создает относительно горизонтальной оси О вращающий момент, равный:
Момент инерции маятника Обербека определится из основного закона динамики вращательного движения, т.е. подставим (3), (4) и (5) в (2’):
Окончательное выражение для вычисления момента инерции маятника Обербека (независимо от наличия грузов на его спицах) будет таким:
момента инерции крестовины. Пусть грузы
Для проверки основного закона динамики вращательного движения необходимо определить моменты инерции грузов на крестовине маятника Обербека, закрепленных на различных расстояниях от оси вращения. Согласно определению (1), момент инерции прямо пропорционален квадрату расстояния до оси вращения О, т.е. для одного и того же тела массы
Замечание. Следует отметить, что в данном рассмотрении мы пренебрегаем силами трения в осях вращающихся деталей установки.
Вопросы к допуску:
1. Какое движение называется вращательным? Можно ли сказать, что движение материальной точки по окружности – вращательное? В чем основное различие в использовании терминов «вращательное движение» и «движение по окружности»? 2. Раскрыть содержание и назначение понятия «момент инерции». 3. Сформулировать и записать основной закон динамики вращательного движения. 4. Пояснить механическую схему установки, назначение ее элементов, принцип работы. 5. Записать основной закон динамики вращательного движения применительно к маятнику Обербека. 6. Пояснить величины, входящие в формулу (6)? Как они измеряются в работе? 7. Связана ли формула (8) с основным законом динамики вращательного движения? Может ли она использоваться для его проверки или же она подтверждает только лишь определение момента инерции? 8. Почему при измерениях момента инерции грузы m должны располагаться симметрично относительно оси вращения? 9. Какие величины в эксперименте изменяются при замене одного шкива другим? Содержание экспериментальных заданий Задание1. Экспериментальная проверка характера зависимости углового ускорения от момента силы ( при условии I=const). 1) Установите на оси крестовину без грузов. 2) Измерьте штангенциркулем диаметры D1 и D2 шкивов. 3) Намотайте нить на один из шкивов, например меньший r1, и подвесьте груз P с mгр. = 200 г к концу нити, предварительно измерив его массу. 4) Измерьте расстояние h от основания груза до площадки (пола, табуретки) по вертикальной линейке. Отметьте допускаемую погрешность Dh и запишите. 5) Отсчитайте по секундомеру время t1 движения груза. Как только груз коснется площадки, прибор придержать за шкив. 6) Повторите опыт 3-4 раза при одной и той же высоте h чтобы уменьшить случайную погрешность при нахождении времени падения груза. 7) Проделайте те же измерения для второго шкива: измерьте время t2 падения груза 200 г при сматывании нити со шкива большего радиуса. 8) Замените груз P на mгр. = 300 г (измерьте массу второго груза на весах!), и проделайте те же измерения для обоих шкивов: получите время падения t3 (для шкива r1) и t4 (для шкива r2). 9) Вычислите для каждого из четырех проделанных опытов моменты сил и соответствующие им угловые ускорения. Занесите все результаты в таблицу 1. Таблица 1
10) Проверить отношения: 11) Вычислите погрешность полученного значения момента инерции крестовины, считая измерения многократными (n=4).
Задание 2. Экспериментальная проверка зависимости момента инерции грузов от расстояния до их вращения (M=const). 1) На стержнях прибора закрепитt грузы 2) Оставив неизменным груз P (m =200 г) на нити, намотанной на один из шкивов r1, провести измерения величин (п. 3, 4, 5, 6 задания 1). Вычислить I1(1). По (7) вычислить момент инерции одного груза I(1). 3) Переместив грузы на расстояние R2, провести снова измерения величин и вычислить I1(2) и вычислите I(2). 4) Проверить зависимость момента инерции от расстояния до оси вращения: Для результатов измерений составите таблицу 2. Таблица 2
!!! Укажите в заголовках столбцов таблицы соответствующие единицы измерения стоящих в них физических величин. 5) Сделайте вывод на основе проделанного сравнения. Соотнесите полученные результаты с возможностью экспериментального подтверждения таким образом основного закона динамики вращательного движения (см. вопрос к допуску №6).
Вопросы к отчету.
1. Дайте понятие о моменте силы, моменте импульса, моменте инерции и единицах их измерений. 2. Сравните второй закон Ньютона для вращательного движения со вторым законом для поступательного движения. Какова роль момента инерции во вращательном движении? 3. Как выражается в работе тангенциальное ускорение точек шкива? Какова его связь с угловым ускорением шкива? 4. Какое направление имеет вектор углового ускорения и вектор момента силы? 5. Какие силы действуют на груз P? 6. Изменится ли угловое ускорение, если изменить груз? Какова зависимость между P и e? 7. Дайте определение механического движения. Что представляет собой вращательное движение? Основные кинематические и динамические параметры вращательного движения. 8. Основная задача механики. Прямая и обратная задачи механики. 9. Физические модели в механике: материальная точка, абсолютно твердое тело, сплошная среда. Границы применимости этих моделей. 10. Центр масс твердого тела. (Центр масс – это единственная точка тела, при приложении к которой внешней силы тело будет двигаться поступательно. При расчетах можно считать, что вся масса тела сосредоточена в этой точке.). Теорема Штейнера (с доказательством). 11. Выведите расчетную формулу (6), пользуясь определениями физических величин и физическими законами. 12. При любом ли расположении масс на крестовине их можно считать точечными?
Лабораторная работа № 2.3. Изучение законов вращательного движения с помощью махового колеса. (Определение момента инерции махового колеса и силы трения в опоре)
Цель работы: вычисление моментов инерции тел правильной геометрической формы; экспериментальное измерение момента инерции махового колеса методом вращения. Приборы и принадлежности: маховое колесо, набор грузов, секундомер, штангенциркуль, разновес, измерительная лента.
|

 ся условиями эксперимента. Для приведения прибора во вращательное движение нить подвеса груза P массой mгр. наматывается на один из шкивов, и затем груз поднимается на некоторую высоту h от поверхности табуретки или пола. Груз отпускается и движется вниз с ускорением a вдоль вертикальной линейки, на которой отмечаются начальное и конечное положения при движении. С помощью секундомера фиксируется точное время движения подвеса. Зная h и время движения груза t, можно вычислить ускорение:
ся условиями эксперимента. Для приведения прибора во вращательное движение нить подвеса груза P массой mгр. наматывается на один из шкивов, и затем груз поднимается на некоторую высоту h от поверхности табуретки или пола. Груз отпускается и движется вниз с ускорением a вдоль вертикальной линейки, на которой отмечаются начальное и конечное положения при движении. С помощью секундомера фиксируется точное время движения подвеса. Зная h и время движения груза t, можно вычислить ускорение: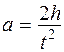 (3).
(3). , где r - радиус шкива, с которого сматывается нить, или, учитывая (3):
, где r - радиус шкива, с которого сматывается нить, или, учитывая (3): (4).
(4). и сила натяжения шнура
и сила натяжения шнура  . По второму закону Ньютона для груза Р в проекции на направление движения:
. По второму закону Ньютона для груза Р в проекции на направление движения: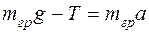 откуда
откуда ,
,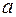 - ускорение движения груза, g - ускорение силы тяжести.
- ускорение движения груза, g - ускорение силы тяжести. или M=mгр.(g - a)r (5).
или M=mгр.(g - a)r (5). Þ
Þ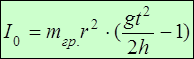 (6) - расчетная формула для
(6) - расчетная формула для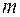 на стержнях располагаются симметрично. Тогда для определения момента инерции груза m необходимо найти сначала момент инерции прибора I0 без грузов, а затем момент инерции прибора с грузами I1, тогда момент инерции каждого груза m будет равен:
на стержнях располагаются симметрично. Тогда для определения момента инерции груза m необходимо найти сначала момент инерции прибора I0 без грузов, а затем момент инерции прибора с грузами I1, тогда момент инерции каждого груза m будет равен: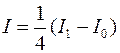 (7).
(7). справедливы соотношения:
справедливы соотношения: ,
,  ,
,  ...
...  или
или (8).
(8).
 и сделать вывод.
и сделать вывод. на одинаковом расстоянии R1 (измерьте его) от оси вращения (проверить состояние безразличного равновесия).
на одинаковом расстоянии R1 (измерьте его) от оси вращения (проверить состояние безразличного равновесия).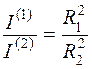 , сравнив величины
, сравнив величины  и
и  .
.


