Краткая теория вопроса. Важным видом движения является движение колебательное, т.е
Важным видом движения является движение колебательное, т.е. периодическое или повторяющееся. Простейшим периодическим изменением служат гармонические колебания. Опр.1 Гармоническим колебанием физической величины х называется процесс изменения ее во времени t no закону
Из определения гармонического колебания следует, что период колебания является наименьшим промежутком времени, по истечении которого движение в точности повторяется. Действительно,
За время t=T совершается одно полное колебание. Амплитуда колебания А равна максимальному значению х. Величина Величина Опр. 2 Физическим маятником называется тело, укрепленное на неподвижной горизонтальной оси, не проходящей через его центр тяжести, и способное совершать колебания относительно этой оси (рис. 2). Докажем, что маятник, отклоненный на малый угол a от положения равновесия, будет совершать гармонические колебания, Обозначим через I момент инерции маятника относительно оси О. Пусть точка C является центром тяжести. Силу тяжести m g можно разложить на две составляющие, одна из которых уравновешивается реакцией опоры. Под действием другой составляющей Здесь а = ОА — расстояние от точки подвеса до центра тяжести. Знак минус выбран потому, что действующая сила направлена в сторону противоположную положительному направлению отклонения маятника. Так как угол a мал, то sin a»a. Подставляя получим:
Можно показать, что частным решением последнего дифференциального уравнения является: Сравнивая (2) и (6), получим:
|

 (1), где А – амплитуда колебания (максимальное значение величины х), Т — период колебания. Величина
(1), где А – амплитуда колебания (максимальное значение величины х), Т — период колебания. Величина  носит название фазы,
носит название фазы,  - начальная фаза.
- начальная фаза.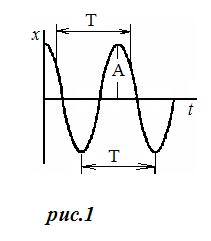 График такого колебания представлен на рис. 1.
График такого колебания представлен на рис. 1.
 (2) называется круговой (циклической) частотой. Если начальная фаза равна
(2) называется круговой (циклической) частотой. Если начальная фаза равна  , то уравнение гармонического колебания записывается в виде:
, то уравнение гармонического колебания записывается в виде: 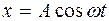 (1’).
(1’).
 маятник приходит в движение. На основании второго закона механики для вращательного движения имеем:
маятник приходит в движение. На основании второго закона механики для вращательного движения имеем:  (3), где угловое ускорение по определению равно:
(3), где угловое ускорение по определению равно:  (4).
(4).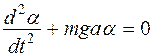 (5).
(5). , если
, если  (6).
(6). (7) Þ следует, что период колебания увеличивается с увеличением момента инерции.
(7) Þ следует, что период колебания увеличивается с увеличением момента инерции.


