Описание установки. Большинство косвенных методов измерения ускорения свободного падения g основано на использовании формулы (7) для периода гармонических колебаний физического
Большинство косвенных методов измерения ускорения свободного падения g основано на использовании формулы (7) для периода гармонических колебаний физического маятника. Однако формула (7) непосредственно для вычисления g не используется, так как момент инерции I и расстояние a
В данной работе это достигается путем использования физического маятника в форме длинного стержня. Маятник представляет собой однородный стержень (рис. 3) с опорной призмой П, которую можно перемещать вдоль стержня и закреплять в любом его месте. Для определения положения призмы на стержне нанесена шкала с делениями через 1 см. Период колебаний маятника, который выражается формулой (7), можно записать в виде:
Из (8) вытекает способ экспериментального определения приведенной длины физического маятника с помощью математического маятника: если взять математический маятник длины L, то период его колебаний будет совпадать с периодом колебания физического маятника с приведенной длиной L, т.е. при одновременном наблюдении их колебания будут оставаться синфазными в течение достаточно большого промежутка времени. Момент инерции стержня относительно оси качания запишем по теореме Штейнера: Для любого тела момент инерции I0 можно представить в виде:
Величина a0 называется радиусом инерции и имеет определенное значение для каждого тела. Для стержня Подставляя (9) и (12) в (10), получим выражение для приведенной длины , и периода колебаний Таким образом, приведенная длина и, следовательно, период колебаний маятника являются функциями расстояния а от центра инерции до оси качания. Из этих формул видно, что L и T стремятся к бесконечности при двух значениях a: при a ®0 и при a ®¥. Для определения значений, при которых период является экстремальным, найдем производную откуда a=± a0. Значит, T=Tмин, если опорная призма закреплена на расстоянии a0» откуда Приведенная длина (рис.4) L=MN+MK, очевидно, что другому периоду колебаний будет соответствовать другая приведенная длина.
После подстановки (15) в (8) получим откуда Формула (16) является расчетной для вычисления ускорения свободного падения. Значения
Вопросы к допуску: 1. Какое движение называется колебаниями? 2. Что такое физический маятник? 3. Дайте определение и запишите формулы для вычисления периода и приведенной длины физического маятника. 4. Что называют радиусом инерции? Чему он равен в случае однородного стержня? 5. Пояснить, что отражено на рис.4. 6. Как с помощью математического маятника найти приведенную длину стержня? 7. Записать расчетную формулу для нахождения ускорения свободного падения и пояснить, как в работе находятся значения входящих в нее величин (из формулы (8) и по (16)). 8. По каким данным и измерениям надо построить график в работе? Как он будет использоваться при достижении цели работы? 9. Меняется ли приведенная длина стержня при различном положении оси качания относительно его верхнего края? Обосновать ответ. Содержание экспериментальных заданий Задание1. Определение приведенной длины стержня с помощью математического маятника. 1) Установите стержень согласно рис.3. Измерьте и запишите расстояние а от оси качания до середины стержня. 2) Используя математический маятник, подберите его длину так, чтобы колебания обоих маятников совершались синфазно. Измерьте полученную длину L математического маятника. 3) Отсчитывая 3 раза время 10-15 колебаний стержня в установленном положении, найти период его колебаний (при малом угле отклонения!!!) 4) Из (8) выразить и найти ускорение свободного падения. 5) Вычислить погрешности полученного результата. 6) Записать ответ с указанием абсолютной и относительной погрешности косвенного измерения g. Задание 2. Построение графика зависимости периода колебаний маятника-стержня от расстояния между верхним концом стержня и осью качания. 1) Опорную призму укрепить на конце стержня. Поместить маятник ребром опорной призмы на подставку и привести в колебательное движение так, чтобы амплитуда колебаний не превышала ~ 60. Это означает, что наибольшее отклонение нижнего конца стержня от положения равновесия не должно превышать 0, 1 расстояния от конца до опорной призмы. 2) Определить секундомером время t десяти полных колебаний. Значения х и t записать в табл. 1. 3) Перемещать опорную призму к середине стержня через 0, 01 м, измеряя для каждого ее положения время 10 полных колебаний и занося результаты измерения в табл. 1. Измерения можно прекратить после того, как получится, что время 10 колебаний стало больше времени, полученного при самом первом измерении, когда опорная призма находилась на конце стержня. Перевертывать маятник и определять периоды для различных положений призмы на другом конце стержня нет необходимости. 4) Вычислить периоды колебаний Т по формуле Т=t/n и занести в таблицу1. Таблица 1.
5) Построить график T=f(x). Для этого по оси абсцисс откладывают расстояние х от конца стержня до опорной призмы, а по оси ординат - соответствующее значение периода. Масштаб по оси ординат следует выбрать по возможности больше, чтобы точнее определить по графику величины L и T. Для этого за начало отсчета по оси ординат нужно взять не нуль, а некоторое значение периода, меньшее Тmin, но близкое к нему. 6) Отметить на оси абсцисс середину стержня и провести через эту точку прямую, параллельную оси ординат. В итоге получится график, показанный на рис.5. 7) По графику определить для 5 различных значения периода соответствующие им значений приведенной длины маятника L, см. ф-лу (15). Для этого нужно провести 5 прямых, параллельных оси абсцисс так, чтобы каждая прямая пересекала построенную кривую в двух точках. Значения Т и L, определенные для каждой такой прямой, записать в табл. 2. 8) По формуле (16) вычислить g для каждого измерения и найти среднее значение
9) Вычислить абсолютную и относительную погрешность по формулам
Таблица 2.
где t(a, n) - коэффициент Стъюдента,
10) Записать конечный результат в виде g =..... ±....... 11) Сформулировать вывод о точности косвенных методов измерения ускорения свободного падения, опробированных в работе.
Вопросы к отчету.
1. Какие колебания называются гармоническими? Дать определение их основных характеристик (амплитуды, фазы, периода, частоты, циклической частоты). 2. При каких условиях колебания физического маятника можно считать гармоническими? 3. Вывести формулу периода колебаний физического маятника. 4. Что называется приведенной длиной физического маятника? 5. Что называется моментом инерции материальной точки? Как вычислить момент инерции твердого тела? Сформулировать теорему Штейнера. 6. Вывести расчетную формулу. 7. Почему для определения g не пользуются непосредственно формулой периода колебаний маятника?
Лабораторная работа № 2.6. Определение ускорения свободного падения с помощью математического маятника.
Цель работы: исследование свойств математического маятника и экспериментальное определение ускорения свободного падения. Приборы и принадлежности: математический маятник, линейка, секундомер.
|

 обычно не могут быть измерены достаточно точно. Поэтому применяются такие методы, которые позволяют исключить данные величины из расчетной формулы для вычисления g.
обычно не могут быть измерены достаточно точно. Поэтому применяются такие методы, которые позволяют исключить данные величины из расчетной формулы для вычисления g.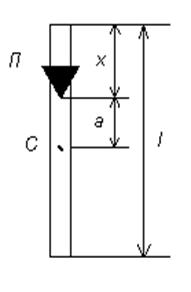 Рис. 3
Рис. 3
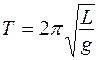 (8), где величина
(8), где величина (9) называется приведенной длиной физического маятника.
(9) называется приведенной длиной физического маятника. (10), где I0 - момент инерции стержня относительно оси, проходящей через центр массы C (середину стержня) параллельно оси качания. Для стержня
(10), где I0 - момент инерции стержня относительно оси, проходящей через центр массы C (середину стержня) параллельно оси качания. Для стержня  (11).
(11). (12).
(12). .
.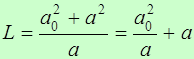 (13)
(13)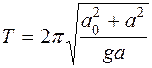 (14)
(14) и приравняем ее к нулю:
и приравняем ее к нулю: ,
, от середины стержня. Второе расстояние a=a0 означает, что если перевернуть стержень, то для точек подвеса, симметричных относительно середины, периоды колебаний будут одинаковы. Из графика (риc. 4) видно, что при увеличении или уменьшении расстояния a по сравнению с a0 период колебания увеличивается. Поэтому одно и то же значение периода, большее чем Tмин, маятник может иметь при двух положениях опорной призмы: при
от середины стержня. Второе расстояние a=a0 означает, что если перевернуть стержень, то для точек подвеса, симметричных относительно середины, периоды колебаний будут одинаковы. Из графика (риc. 4) видно, что при увеличении или уменьшении расстояния a по сравнению с a0 период колебания увеличивается. Поэтому одно и то же значение периода, большее чем Tмин, маятник может иметь при двух положениях опорной призмы: при  и
и  . Для этих положений опорной призмы будут одинаковы и приведенные длины маятника, что следует, из формулы (8):
. Для этих положений опорной призмы будут одинаковы и приведенные длины маятника, что следует, из формулы (8):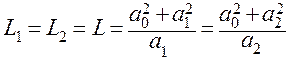 ,
, . Тогда
. Тогда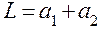 . (15)
. (15) Рис. 4.
Рис. 4.
 ,
,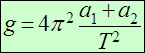 . (16)
. (16) Рис. 5.
Рис. 5.
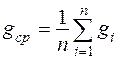

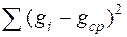 =…
=…
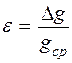 .
.


