Описание прибора и теория метода
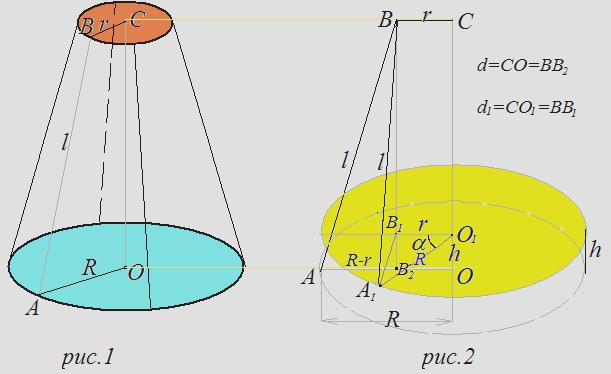
Одним из методов определения момента инерции тел является метод трифилярного подвеса. Трифиляр представляет собой круглую платформу, подвешенную на 3-х симметрично расположенных нитях (рис.1). Верхние концы нитей симметрично прикреплены к диску. Платформа может совершать крутильные колебания вокруг вертикальной оси, перпендикулярной к ее плоскости и проходящей через ее центр. Вращательный импульс, необходимый для начала крутильных колебаний, сообщается платформе путем поворота верхнего диска вокруг его оси. При крутильных колебаниях платформы ее центр масс перемещается по оси вращения, занимая наивысшее положение при максимальном отклонении платформы от положения равновесия и наинизшее при прохождении положения равновесия. Если платформа массы m, вращаясь в одном направлении, поднялась на высоту h, то приращение потенциальной энергии будет равно Вращаясь в другом направлении платформа придет в положение равновесия с кинетической энергией, равной Пренебрегая работой сил трения, на основе закона сохранения механической энергии имеем: Если l – длина нитей подвеса, R – радиус платформы, r – радиус верхнего диска, то по рис.2 определим h.
В положении равновесия центр нижнего диска находится в точке О. Рассмотрим радиус диска ОА. При его повороте на угол a центр нижнего диска переходит в точку О1 и приподнимается на расстояние Далее требуется провести ряд математических преобразований, чтобы выразить приблизительно высоту подъема h через радиусы дисков и длину нитей, т.е. через R, r и l. Запишем:
Подставляя (3) в (1), получаем:
данным методом. Здесь I – суммарный момент инерции платформы (нижнего диска трифиляра), т.е. в случае. когда на ней находится исследуемое тело, формула (6) дает значение момента инерции платформы вместе с находящимся на ней телом. Причем на опыте это значение будет разным при различных положениях тела на платформе (это следует из определения момента инерции тела). Учитывая свойство аддитивности величины момента инерции, можно найти момент инерции одного лишь тела
при данном его положении относительно оси вращения.
Метод трифилярного подвеса позволяет проверить теорему Штейнера. Для этого необходимо иметь два одинаковых тела массой
Вопросы к допуску: 1. Что такое трифилярный подвес? Из чего он состоит? 2. Какое движение совершает нижний диск трифиляра в данном методе? Записать уравнение этого движения и пояснить входящие в него величины. 3. Чем обосновано приближение в формуле (3)? Пояснить это с математической и физической точек зрения. 4. Как связан период колебаний платформы с ее моментом инерции? 5. Дать определение момента инерции и пояснить что обозначено буквой I в формуле (6). В чем состоит свойство аддитивности физической величины I? 6. Сформулировать теорему Штейнера. Как можно убедиться в ее справедливости с помощью описанного в работе метода? 7. Вывести формулу (4). Как получено ее математическое решение?
Содержание экспериментальных заданий. Задание 1. Определение момента инерции платформы 1) Измерьте параметры трифиляра: R, r, l, m. 2) Приведите платформу трифиляра в движение, соответствующее крутильным колебаниям. 3) Измерьте время, за коротое будет совершено 20-30 колебаний. Колебания отсчитываются по прохождению положения равновесия какой-либо точки диска. 4) Найдите период колебаний Т. 5) По формуле (6) найдите 6) Повторите опыт 3 раза, начиная с пункта 1) (каждый раз заново приводя платформу в движение!). Вычислите погрешность отдельного косвенного измерения и результата. Результаты измерений и вычислений занесите в таблицу. Задание 2. Определение момента инерции исследуемого образца. 1) Выберите положение оси, относительно которой требуется найти момент инерции данного образца (например, взять ось его симметрии или ось, проходящую через центр тяжести образца, если его (центра тяжести) положение легко определимо или задано). 2) Поместите образец на платформу трифиляра так, чтобы ось ее вращения совпадала с осью из пункта 1). 3) Приведите платформу трифиляра в движение, соответствующее крутильным колебаниям. 4) Измерьте время, за которое будет совершено 20-30 колебаний. Колебания отсчитываются по прохождению положения равновесия какой-либо точки диска. 5) Найдите период колебаний Т платформы с грузом. 6) По формуле (6) найдите I. 7) Вычислите момент инерции образца относительно выбранной в пункте 1) оси по свойству аддитивности: см. формулу (7). 8) Данные занести в таблицу. Оценить погрешность результата измерения. 9) Если образец имеет одну из геометрически правильных форм, то сравните полученный результат с теоретическими расчетами момента инерции тела данной геометрической формы. Задание 3. Проверка выполнения теоремы Штейнера. 1) Взять 2 одинаковых (например, цилиндрических) образца и найти момент инерции I1 каждого из них как описано в задании 2, выбрав в качестве оси вращения ось, проходящую через их центр инерции. 2) Найти массу mобразца каждого образца. 3) Поместить образцы на одном диаметре платформы трифиляра симметрично друг другу относительно центра платформы. измерить расстояние а от центра инерции образца до центра платформы. 4) Приведите платформу трифиляра в движение, соответствующее крутильным колебаниям. 5) Измерьте время, за которое будет совершено 20-30 колебаний. 6) Найдите период колебаний Т нагруженной платформы. 7) По формуле (6) найдите I. 8) Вычислите момент инерции образца на расстоянии а от оси вращения: 9) Подставить полученные значения в формулу: 10) Сравнить значения правой и левой частей этого равенства с учетом величины погрешности измерений. 11) Сделать вывод о выполнении теоремы Штейнера в данном эксперименте.
Вопросы к отчету: 1. Как определяется момент инерции материальной точки и твердого тела? 2. Выведите формулу кинетической энергии вращающегося твердого тела. 3. Объяснить возможность применения закона сохранения энергии к выводу формулы (1). 4. Докажите теорему Штейнера. 5. В чем отличие крутильных колебаний от колебаний физического маятника? 6. Под действием какой силы трифилярный подвес совершает крутильные колебания? 7. Почему для определения периода надо измерять время большого числа колебаний? 8. как изменяется период крутильных колебаний трифилярного подвеса от расположения масс на платформе? 9. Что служит источником погрешностей измерений в данной работе?
Лабораторная работа № 2.5. Определение ускорения свободного падения с помощью физического маятника.
Цель работы: исследование свойств физического маятника (построение графика зависимости периода колебаний маятника-стержня от расстояния между верхним концом стержня и осью качания) и экспериментальное определение ускорения свободного падения. Приборы и принадлежности: однородный стержень с отверстиями, опорная призма, математический маятник, линейка, секундомер.
|

 , где g – ускорение свободного падения.
, где g – ускорение свободного падения. , I – момент инерции платформы,
, I – момент инерции платформы,  - угловая скорость платформы в момент достижения ею положения равновесия.
- угловая скорость платформы в момент достижения ею положения равновесия. или
или  (1).
(1).
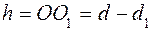 , где d и d1 - расстояние между верхним и нижним дисками соответственно в положении равновесия и при повороте на угол a нижнего диска относительно верхнего.
, где d и d1 - расстояние между верхним и нижним дисками соответственно в положении равновесия и при повороте на угол a нижнего диска относительно верхнего. (2). Из прямоугольного треугольника ВВ2А:
(2). Из прямоугольного треугольника ВВ2А:  , аналогично из ВВ1А1 найдем d1, где В1А1 выражаем по теореме косинусов из треугольника В1О1А1:
, аналогично из ВВ1А1 найдем d1, где В1А1 выражаем по теореме косинусов из треугольника В1О1А1:  . Подставим в (2):
. Подставим в (2): (3), где приближенные замены оправданы в случае большой длины нитей l и малых углах отклонений a при крутильных колебаниях нижнего диска трифиляра (это дает приближение данного движения в форме гармонических колебаний).
(3), где приближенные замены оправданы в случае большой длины нитей l и малых углах отклонений a при крутильных колебаниях нижнего диска трифиляра (это дает приближение данного движения в форме гармонических колебаний). . Продифференцировав это выражение по времени, сократив на
. Продифференцировав это выражение по времени, сократив на 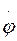 и поделив на I, получим уравнение движения системы:
и поделив на I, получим уравнение движения системы:  (4). Решение этого уравнения имеет вид:
(4). Решение этого уравнения имеет вид: , где
, где  - циклическая частота крутильных колебаний нижнего диска,
- циклическая частота крутильных колебаний нижнего диска,  - начальная фаза, задающая положение нижнего диска в начальный момент времени. Тогда период колебаний системы равен:
- начальная фаза, задающая положение нижнего диска в начальный момент времени. Тогда период колебаний системы равен:  (5). Разрешив относительно I, найдем выражение для момента инерции системы:
(5). Разрешив относительно I, найдем выражение для момента инерции системы: (6) – формула для определения момента инерции
(6) – формула для определения момента инерции (7)
(7) . Располагая их на платформе так, чтобы их центры масс лежали на оси вращения, а затем симметрично по диаметру платформы, определяют по (6) моменты инерции I 1 и I 2 в обоих случаях, тогда в соответствии с теоремой Штейнера:
. Располагая их на платформе так, чтобы их центры масс лежали на оси вращения, а затем симметрично по диаметру платформы, определяют по (6) моменты инерции I 1 и I 2 в обоих случаях, тогда в соответствии с теоремой Штейнера:  , где а – расстояние от оси вращения до центра масс тела.
, где а – расстояние от оси вращения до центра масс тела. без груза.
без груза. .
.
 .
.


