Краткая теория вопроса. Вращательное движение осуществляют всегда твердые тела, имеющие конечные размеры (не материальная точка!)
Вращательное движение осуществляют всегда твердые тела, имеющие конечные размеры (не материальная точка!). Изучая вращательное движение, твердое тело рассматривают или как систему материальных точек или как сплошную среду, заполняющую объем тела. В любом случае по отношению к оси вращения имеется некоторое распределение суммарной массы этого тела. Момент инерции является физической величиной, характеризующей инертность тела к изменению им угловой скорости под действием вращающего момента. Угловая скорость и вращающий момент – также величины, заданные относительно оси вращения. Опр. 1 Моментом инерции материальной точки относительно какой-либо оси называется произведение ее массы на квадрат расстояния до этой оси:
Опр. 3 Для тела, понимаемого как сплошная среда с плотностью
где r – расстояние от элемента объема dV до оси, относительно которой вычисляется момент инерции тела. Момент инерции относительно данной оси, как и масса тела, не зависит от характера движения, а зависит от размеров, формы и плотности тела. Если момент инерции относительно оси, проходящей через центр массы тела, равен Основной закон динамики для вращательного движения записывается аналогично второму закону Ньютона с эквивалентной заменой величин, описывающих поступательное движение, на величины, характеризующие вращательное движение: Величина Для замкнутой системы имеет место закон сохранения момента Итак, в случае вращательного движения момент инерции играет такую же роль, как масса при поступательном движении, а угловая скорость — роль линейной. Математическая форма записи основных закономерностей для поступательного и вращательного движения остается неизменной, что видно из следующей таблицы.
|

 (1)
(1)
 Опр. 2 Моментом инерции тела (понимаемого как совокупность материальных точек или частиц) относительно какой-либо оси называется сумма моментов инерции всех частиц тела (рис. 1) относительно этой же оси:
Опр. 2 Моментом инерции тела (понимаемого как совокупность материальных точек или частиц) относительно какой-либо оси называется сумма моментов инерции всех частиц тела (рис. 1) относительно этой же оси: (2)
(2) , момент инерции может быть вычислен путем интегрирования по объему тела:
, момент инерции может быть вычислен путем интегрирования по объему тела: (3),
(3), , то момент инерции
, то момент инерции  относительно любой другой параллельной оси может быть вычислен на основании теоремы Гюйгенса-Штейнера:
относительно любой другой параллельной оси может быть вычислен на основании теоремы Гюйгенса-Штейнера:  (4), где d — расстояние между осями.
(4), где d — расстояние между осями. (5), где
(5), где 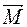 — сумма моментов сил, действующих на тело,
— сумма моментов сил, действующих на тело,  — угловая скорость вращения. Если
— угловая скорость вращения. Если  или
или  .
. называется моментом количества (вращательного) движения. Таким образом, если на вращающееся тело не действует вращающий момент, оно будет вращаться неопределенно долго, сохраняя постоянным имеющийся у него момент количества движения.
называется моментом количества (вращательного) движения. Таким образом, если на вращающееся тело не действует вращающий момент, оно будет вращаться неопределенно долго, сохраняя постоянным имеющийся у него момент количества движения.


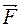


 или
или 






