Мгновенное ускорение
a x = 4. При криволинейном движении ускорение можно представить как сумму нормальной
Абсолютное значение этих ускорений а n = v2/R; a τ = d v /d t; где R – радиус кривизны в данной точке траектории. 5. Кинематическое уравнение равномерного движения материальной точки вдоль оси х (v = const, a = 0) х = х 0 + vt, где х 0 – начальная координата, t – время. 6. Кинематическое уравнение равнопеременного движения вдоль оси х (а = const) x = x 0 + v 0 t + at 2/2, где v 0 – начальная скорость, t – время. Скорость точки при равнопеременном движении v = v 0 + at. 7. Положение твердого тела (при заданной оси вращения) определяется углом поворота (или угловым перемещением)
Угловая скорость
Угловое ускорение
Угловое перемещение, угловая скорость и угловое ускорение являются псевдовекторами, их направления совпадают с осью вращения и определяются по правилу правого винта. 8. Кинематическое уравнение равномерного вращения (ω = const, ε = 0) φ = φ 0 +ω t, где φ 0 – начальное угловое перемещение; t – время. 9. Т - период вращения (время одного полного оборота) Т = t /N; ν – частота вращения (число оборотов в единицу времени) ν = N / T или ν = 1/ Т, где N – число оборотов, совершаемых телом за время t, ω = 10. Кинематическое уравнение равнопеременного вращения (ε = const) φ = φ 0 + ω 0 t + ε t 2/2, где ω 0 – начальная угловая скорость, φ = 2π N. Угловая скорость тела при равнопеременном вращении ω = ω 0 + ε t. 11. Связь между линейными и угловыми величинами, характеризующими вращение материальной точки: S = φ R; v = wR; a t = eR; a n =
|

 ,
,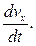
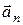 и тангенциальной
и тангенциальной  составляющих
составляющих
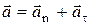 .
. ,
, . Кинематическое уравнение вращательного движения:
. Кинематическое уравнение вращательного движения: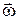 =
= 
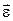 =
= 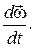
 .
.



