ВВЕДЕНИЕ. А.И. Аркуша «Техническая механика», Москва «Высшая школа», 2003
А.И. Аркуша «Техническая механика», Москва «Высшая школа», 2003
Практическая работа № 6
Тема: Растяжение, сжатие. Построение эпюр продольных сил, нормальных напряжений и удлинений или укорочений бруса. Цель работы: 1.Приобретение практических навыков и умений по определению значений продольных сил, нормальных напряжений и удлинений или укорочений бруса аналитическим и графическим способами. 2.Развитие самостоятельности и точности в выполнении расчётов и графических построений.
Практическая работа № Тема: Цель:
Кручением называют такой вид нагружения бруса, при котором в его поперечных сечениях возникает только один внутренний силовой фактор — крутящий момент Мк (или Мг). Крутящий момент в произвольном поперечном сечении бруса равен алгебраической сумме внешних моментов, действующих на отсеченную часть: Будем считать крутящий момент положительным, если для наблюдателя, смотрящего на прове Соответствующий внешний момент направлен против часовой стрелки (рис. 13). В третьей задаче Необходимо выполнить проектный расчет вала круглого поперечного сечения из условий прочности и из условий жесткости; из двух полученных значений диаметров следует выбрать наибольшее значение..
Последовательность решения задачи: 1.Определить внешние скручивающие моменты по формуле
2. Определить уравновешивающий момент, используя уравнение равновесия 3. Пользуясь методом сечений, построить эпюру крутящих моментов по длине вала. 4. Для участка вала, в котором возникает наибольший крутящий момент, определить диаметр вала для круглого сечения из условий прочности и жесткости.
Из двух полученных диаметров вала выбрать наибольший. Пример 9. Для стального вала (рис. 10) круглого поперечного сечения постоянного по длине (рис. 10, а) требуется:
Рис 10 Рис 11
1. Определить значения моментов M2 и M3, соответствующие передаваемым мощностям Р2 и Р3, а также уравновешивающий момент М\. 2. Построить эпюру крутящих моментов. 3. Определить требуемый диаметр вала из расчетов иа проч-. ность и жесткость, если = 52 кВт; Р3=50 кВт; Окончательное значение диаметра округлить до ближайшего четного (или оканчивающего на пять) числа. Решение: 1. Определяем величины внешних скручивающих моментов М2 и М3:,
2. Определяем уравновешивающий.момент М1:
3. Строим эпюру M1 (рис. 14, 6). 4. Определяем диаметр вала из условий прочности и жесткости. M2max = 5100 H-M (Рис. 10, б).
Требуемый размер сечения получился больше из расчета на прочность, поэтому его принимаем как окончательный: d = 95 мм.
Таблица 1 - Варианты к задаче
Вопросы для самоконтроля:
СПИСОК ЛИТЕРАТУРЫ 1. Ицкович Г. М. Сопротивление материалов. М., 1982. 2. Аркуша А. И., Фролов М. И. Техническая механика. М.., 1983. 3. Мовнин М. С, Израелит А. Б. Сопротивление материалов. Л., 1972. 4. Ицкович Г. М., Винокуров А. И., Барановский Н. В. Сборник задач по сопротивлению материалов. Л., 1965, 1970, 1973. 5. Сборник задач по технической механике Багреев В. В., Винокуров А. И., Киселев В. А. и др. М., 1973.
Практическая работа № Тема: Цель: Изгиб — это такой вид деформации бруса, при котором в его поперечных сечениях возникают изгибающие моменты. В большинстве случаев одновременно с изгибающими моментами возникают и поперечные силы; такой изгиб называют поперечным; если поперечные силы не возникают, изгиб называют чистым. Изгибающий момент в произвольном поперечном сечении бруса численно равна алгебраической сумме внешних сил, действующих на отсеченную часть: Правило знаков для поперечной силы: силам, поворачивающим отсеченную часть балки относительно рассматриваемого сечения по ходу часовой стрелки, приписывается знак плюс (рис. 15, а), а силам, поворачивающим отсеченную часть балки относительно рассматриваемого сечения против хода часовой стрелки, приписывается знак минус (рис, 15, б). Правило знаков для изгибающих моменте: внешним моментам, изгибающим мысленно закрепленную в рассматриваемом сечении отсеченную часть бруса выпуклостью вниз, приписывается знак плюс (рис. 16, а), а моментам, изгибающим отсеченную часть бруса выпуклостью вверх. — знак минус (рис. (1б, б.) Между выражениями изгибающего момента Мх, поперечной силы Qy и интенсирностыо распределенной нагрузки д существуют дифференцилльные зависимости:
На основе метода сечений и дифференциальных зависимостей устанавливается взаимосвязь эпюр Мх и Qy между собой и с внешней нагрузкой, поэтому достаточно вычислить ординаты эпюр для характерных сечений и соединить их линиями. Характерными являются сечения балки, где приложены сосредоточенные силы и моменты (включая опорные сечения), а также сечения, ограничивающие участки с равномерно распределенной нагрузкой.
Рис 16 Рис 18
Приведем некоторые правила построения эпюр. Для эпюры поперечных сил: 1. На участке, нагруженном равномерно распределенной нагрузкой, эпюра изображается прямой, наклоненной к оси балки. 2. На участке, свободном от распределенной нагрузки, эпюра изображается прямой, параллельной оси балки. 3. В сечении балки, где приложена сосредоточенная пара сил, поперечная сила не изменяет значения. 4. В сечении, где приложена сосредоточенная сила, значение поперечной силы меняется скачкообразно на значение, равное приложенной силе. 5 В концевом сечении балки поперечная сила численно равна сосредоточенной силе (активной или реактивной), приложенной в этом сечении Если в концевом сечении балки не приложена сосредоточенная сила, то поперечная сила в этом сечении равна нулю. Для эпюры изгибающих моментов: 1. На участке, нагруженном равномерно распределенной нагруз кой, эпюра моментов изображается квадратичной параболой. Выпуклость параболы направлена навстречу нагрузке. 2. На участке, свободном от равномерно распределенной нагрузки, эпюра моментов изображается прямой линией. 3. В сечении балки, где приложена сосредоточенная пара сил, изгибающий момент меняется скачкообразно на значение, равное моменту приложенной пары. 4. Изгибающий момент в концевом сечении балки равен нулю, если в нем не приложена сосредоточенная пара сил. Если же в концевом сечении приложена активная или реактивная пара сил, то изгибающий момент в сечении равен моменту приложенной пары. 5. На участке, где поперечная сила равна нулю, балка испытывает чистый изгиб, и эпюра изгибающих моментов изображается прямой, параллельной оси балки. 6. Изгибающий момент принимает экстремальное значение в сечении, где эпюра поперечных сил проходит через нуль, меняя знаки с «+» на «—» или с «—» на «+». В рассматриваемой задаче требуется построить эпюры поперечных сил и изгибающих моментов, а также подобрать размеры поперечного сечения балки, выполненной из прокатного профиля — двутавра. Условие прочности для балок с сечениями, симметричными относительно нейтральной оси, имеет вид:
где Wx — осевой момент сопротивления сечения. Для подбора сечения балки (проектного расчета) из условия прочности определяют необходимое значение осевого момента сопротивления:
По найденному моменту сопротивления Wx подбирают соответствующее сечение по сортаменту (см. приложение 1). Для закрепленной одним концом балки строить эпюры целесообразно со свободного конца (чтобы избежать определения опорных реакций в заделке). Последовательность решения задачи: 1. Балку разделить на участки по характерным сечениям. 2. Определить вид эпюры поперечных сил на каждом участке в зависимости от внешней нагрузки, вычислить поперечные силы в характерных сечениях и построить эпюру поперечных сил. 3. Определить вид эпюры изгибающих моментов на каждом участке в зависимости от внешней нагрузки, вычислить изгибающие моменты в характерных сечениях и построить эпюру изгибающих моментов. 4. Для данной балки, имеющей по всей длине постоянное поперечное сечение, выполнить проектный расчет, т. е. определить W, в опасном сечении, где изгибающий момент имеет наибольшее по модулю значение.
Пример 10. Для заданной консольной балки (поперечное сечение-двутавр, [σ ] = 160 МПа) построить эпюры Qv и Мх и подобрать сечение по сортаменту. 1. Делим балку на участки по характерным точкам О, В С D (рис. 17, а).
Рис. 17
2. Определяем ординаты и строим эпюру QB (рис. 17, 6):
Для определения экстремального значения момента в сечении К, где
В соответствии с ГОСТ 8239—72 выбираем двутавр № 30. (См. приложение 1.)
Пример 11. Для заданной двухопорной балки (рис. 18, а) определить реакции опор, построить эпюры поперечных сил, изгибающих
Рис 18
моментов и определить размеры поперечного сечения (Л, Ь, d) в форме прямоугольника или круга, приняв для прямоугольника
Так как реакция Rd получилась со знаком минус, то изменяем ее первоначальное направление на противоположное. Истинное направление реакции Проверка: вие статики 2 У выполняется, следовательно, реакции опор определены верно. При построении эпюр используем только истинные направления реакций опор. 2. Делим балку на участки по характерным точкам О, В, С, D (рис. 18, 6). 3. Определяем ординаты и строим эпюру Qv (рис. 18, в) слева направо:
4. Вычисляем ординаты и строим эпюру Мх (рис. 18, г):
5. Вычисляем размеры сечения данной балки из условий прочности на изгиб по двум вариантам: а) сечение — прямоугольник с заданным соотношением сторон (рис. 18, е); б) сечение —круг (Рис 18, д). Вычисление размеров прямоугольного сечения:
Таблица 1 - Варианты к задаче
Вопросы для самоконтроля:
СПИСОК ЛИТЕРАТУРЫ 1. Ицкович Г. М. Сопротивление материалов. М., 1982. 2. Аркуша А. И., Фролов М. И. Техническая механика. М.., 1983. 3. Мовнин М. С, Израелит А. Б. Сопротивление материалов. Л., 1972. 4. Ицкович Г. М., Винокуров А. И., Барановский Н. В. Сборник задач по сопротивлению материалов. Л., 1965, 1970, 1973. 5. Сборник задач по технической механике Багреев В. В., Винокуров А. И., Киселев В. А. и др. М., 1973.
Практическая работа № 11
Тема: «Совместное действие изгиба и кручения» Цель работы: «Применяя гипотезы прочности, определить диаметр балки при совместном действии изгиба и кручения»
СОДЕРЖАНИЕ Стр.
ВВЕДЕНИЕ Основным методом исследования в физике является эксперимент, т.е. наблюдение исследуемого явления в точно контролируемых условиях. Лабораторный практикум дает возможность студентам не только изучить экспериментально важнейшие физические явления, но и научиться обращаться с разнообразными, в том числе с самыми современными, физическими приборами. При этом физика представляется студентам уже не просто как набор формул и абстрактных понятий, а как совокупность реально воспроизводимых эффектов, управление которыми лежит в основе инженерной деятельности. Работа на экспериментальной установке не принесет никакой пользы, если экспериментатор не будет четко представлять, какую задачу и какими методами он будет ее решать. Поэтому непременным условием выполнения лабораторного практикума является предварительная подготовка, т.е. изучение теории и методики эксперимента. Описание всех лабораторных работ выполнены в единой последовательности: название работы, перечень приборов и принадлежностей, теоретическое введение, описание установки и метода измерения, выполнение работы, контрольные вопросы.
|
(имеется в виду, что плоскости действия всех внешних скручивающих моментов Mt перпендикулярны продольной оси бруса).
денное сечение, он представляется направленным по часовой стрелке.
, где Р — мощность, со — угловая скорость.
так как при равномерном вращении вала алгебраическая сумма приложенных к нему внешних скручивающих (вращающих) моментов равна нулю.
=30 МПа; 
=0, 02 рад/м; Р2: -
=20 рад/с; G=8-104 МПа. G=8*104 МПа.
в произвольном поперечном сечении бруса численно равен алгебраической сумме моментов внешних сил, действующих на отсеченную часть, относительно центра тяжести сечения: 
. Поперечная сила
. Причем все внешние силы и моменты действуют в главной продольной плоскости бруса и расположены перпендикулярно продольной оси бруса.
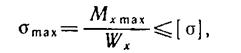
=0, определяем длину КВ.
подобен 
(рис. 17, б), отсюда:
. Считать 
=160 МПа. 1. Определяем опорные реакции и проверяем их найденные значения:
— вниз (рис. 18, 6).
Усло-
