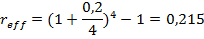Основные инструменты учета стоимости денег во времени
Одной из базовых концепций корпоративных финансов является концепция изменения ценности (стоимости) денег во времени. Это означает, что денежные средства, которые выплачиваются сегодня, имеют другую реальную ценность, чем те, которые будут выплачены в будущем. Действительно, у нас всегда имеется несколько вариантов вложения имеющегося капитала: - его можно использовать его в виде инвестиций в развитие производства, однако, отдача на вложенный капитал откладывается на определенный период; - можно просто держать имеющиеся средства дома в виде наличных денег - при этом сохраняется их номинальная величина, но деньги не «работают», не приносят прибыли, при этом денежные средства обесцениваются под влиянием инфляции; - можно поместить деньги в банк или же вложить в ценные бумаги, начинающие приносить определенную прибыль (процент) сразу же, то есть инвестировать их и получить доход на вложенный капитал. Это многовариантность использования капитала заставляет нас определять издержки упущенной выгоды, связанные с тем или иным вариантом использования денежных средств. По сути дела, речь идет об упущенных возможностях получения выгоды инвестирования денежных средств сегодня (opportunity costs) в связи с тем, что деньги поступят через определенный промежуток времени. Будущая стоимость денежных средств (future value), FV – это сумма денег, которая будет получена в результате их инвестирования на определенный период времени в будущем при определенной процентной ставке. Процесс вычисления будущей стоимости называется компаундированием. Основной формулой, позволяющей рассчитывать будущую стоимость денежных средств, выступает коэффициент накопления. Коэффициент накопления (сложного процента, будущей стоимости) kk показывает будущую стоимость одной денежной единицы по прошествии заданного числа периодов времени t и при заданной процентной ставке r[13]. Формула для расчета при условии дискретного начисления процентов имеет следующий вид:
Процесс начисления процентов на сумму инвестиций и проценты, полученные в предыдущем периоде, называется капитализацией процентов. Эффект капитализации невелик при прошествии короткого периода времени и проявляется по-настоящему при долгосрочных инвестициях. Если имеет место несколько периодов начисления в год, необходимо разделять эффективную и номинальную процентные ставки. Пусть номинальная годовая ставка процента равна rN, количество периодов начисления процентов в год - m, тогда эффективная годовая ставка процента rэф будет определяться по формуле:
Текущая (современная, приведенная) стоимость денежных средств (present value), PV означает сегодняшнюю стоимость сумм, которые будут получены в будущем (через определенный период времени). Расчет текущей стоимости денежных сумм осуществляется на основе коэффициента дисконтирования. Дисконтирование – это вычисление текущей стоимости некой денежной суммы. Коэффициент дисконтирования (приведения сумм, получаемых в будущем, к настоящему моменту) kd показывает сегодняшнюю стоимость 1 денежной единицы, которая будет получена через t периодов времени при процентной ставке r. К расчету этого коэффициента существует несколько подходов. Обычно поток платежей и поступлений рассматривается как дискретный (прерывный): итоги подводятся на конец каждого года (квартала, месяца), и полученные значения величины денежных потоков приводятся к текущему моменту времени исходя из формулы сложного процента.
Нетрудно заметить, что коэффициент дисконтирования выполняет функции, противоположные коэффициенту сложного процента, а следовательно, рассчитывается как обратная ему величина:
Если поток платежей и поступлений рассматривается как непрерывный, дисконтирование проводится на основе непрерывного годового коэффициента дисконтирования kdн, рассчитываемого по формуле:
Для перехода от номинальной процентной ставки при непрерывном начислении процента к эффективной процентной ставке и обратно используются следующие формулы:
Коэффициент сложного процента при непрерывном начислении процента будет рассчитываться по формуле:
Кроме двух названных коэффициентов, важное значение в инвестиционных и финансовых расчетах имеют аннуитеты, выражающие одинаковые по величине денежные потоки, поступающие или выплачиваемые в течение фиксированного периода времени Т при процентной ставке r, отражающей условия возможного инвестирования. Коэффициент аннуитета ka показывает размер постоянных ежегодных денежных потоков, современная стоимость которых равна одной денежной единице для заданного количества лет и при заданной процентной ставке r:
Коэффициент обратного аннуитета (дисконтирования повторяющихся сумм) koa показывает современную стоимость этих ежегодных денежных потоков:
Данный коэффициент применяется в тех случаях, когда известно, например, что сумма поступлений и платежей за каждый год осуществления инвестиционного проекта будет постоянной. Учет эффекта процентных начислений позволяет сделать два основных вывода о современной стоимости сумм, получаемых по прошествии определенного времени. 1. Текущая стоимость некоторой суммы будет тем ниже, чем более отдален во времени момент ее получения. 2. Текущая стоимость данной суммы при фиксированном сроке ее получения будет тем ниже, чем будет выше ставка учетного процента. Важное значение для точности финансовых расчетов имеет учет изменения рыночных цен на отдельные виды товаров и услуг и общего снижения стоимости денег (инфляции). Инфляция проявляется в увеличении цен на товары и обычно измеряется индексами цен за определенный период и их динамикой. Индекс роста потребительских цен является наиболее часто применимым на практике индикатором инфляции. На отраслевом уровне определяются так называемые производственные индексы цен. Учетная ставка процента и уровень ожидаемой прибыли от инвестиционной деятельности зависят от темпов инфляции. Коэффициент дисконтирования должен реально отражать снижение стоимости денежных потоков с течением времени. Необходимость учета темпов инфляции требует корректировки значения учетного процента. Рекомендуемая в экономической литературе формула для учета влияния инфляции на реальную ставку процента (формула Фишера) выглядит следующим образом:
где r - расчетная (реальная) процентная ставка, R - рыночная (номинальная) ставка процента, I - темпы инфляции за период. Как легко можно убедиться путем осуществления расчетов, в данном случае r - это реальный уровень доходности инвестиций с учетом инфляции, который будет значительно ниже номинальной процентной ставки, и, таким образом, его использование для расчета коэффициента дисконтирования приведет к значительному искажению результата. Мы предлагаем, исходя из предположения о том, что можно относительно точно спрогнозировать темпы инфляции за период (I) и определить желаемый уровень реальной доходности инвестиций (R) рассчитывать учетную ставку процента по формуле:
Обобщенно информация о коэффициентах, позволяющих учитывать изменение ценности денег во времени, представлена в таблице 4.3 Таблица 4.3 Коэффициенты, учитывающие изменение ценности денег во времени
|

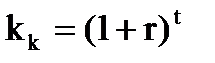 . (4.1)
. (4.1)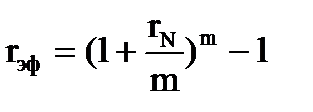 (4.2)
(4.2)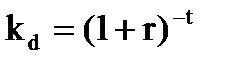 (4.3)
(4.3) .
. . (4.4)
. (4.4)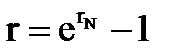 ,
,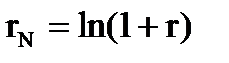 .
.
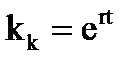 . (4.5)
. (4.5)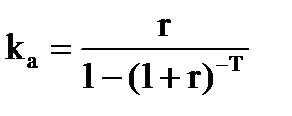 . (4.6)
. (4.6) . (4.7)
. (4.7)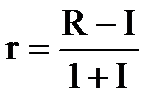 , (4.8)
, (4.8)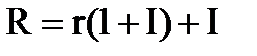 . (4.9)
. (4.9)
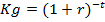


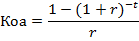

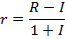
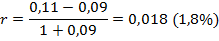
 где rn – номинальная процентная ставка,
m – количество выплат в течение года
где rn – номинальная процентная ставка,
m – количество выплат в течение года