Критерий роста трещины

Увеличение длины трещины происходит тогда, когда величина G равна энергии, необходимой для роста трещины. В истинно хрупких материалах, например таких, как стекло, энергией, оказывающей влияние на рост трещины, является поверхностная энергия, необходимая для образования новых свободных поверхностей, т. е.

 

Уравнение (5.1) можно разрешить с помощью уравнений (5.6) и (5.15), откуда получаем:

 

что и является критерием Гриффитса [1, 2].

Ирвин [6] и Орован [7] заметили, что энергия, необходимая для роста трещины в металле, намного превосходит поверхностную энергию, необходимую для обра-

зования новых свободных поверхностей. В металлах перед трещиной образуются пластические деформации, и во время распространения трещины энергия расходуется на образование зоны пластичности при вершине распространяющейся трещины. Если пластическая энергия R для одинаковых приращений размеров различных трещин одинакова, то величина R p=s dWIda остается постоянной. Из эксперимента следует, что это приблизительно верно для трещин,

распространяющихся при плоской деформации: образцы с трещина-- ми различных размеров, как оказывается, разрушаются при одних и тех же значениях G. Это критическое значение G обозначают как G_k; = (1 -v*)Kl/E.

Следовательно, в случае плоской деформации R р= dWIda — G\_c, откуда следует, что

Критерий разрушения можно изобразить графически так, как показано на рис. 5.4. Сопротивление росту трещины R не зависит

от размера трещины; поэтому эта величина представлена на рисунке прямой горизонтальной линией R τ = G\_c. Интенсивность выделения энергии

(5.18)

При заданном напряжении a_i скорость выделения энергии пропорциональна размеру трещины а. Для этого случая величина G представлена на рисунке линией О А. Если трещина имеет размер о_ь то скорость выделения энергии при напряжении σ ₂ представлена точ-

кой В. При увеличении напряжения от σ ₂ до a_t величина G увеличивается от точки В до точки А. В точке А может произойти увеличение размера трещины, так как выполняется условие G > = R. В более длинной трещине размера а₂ эта ситуация возникает уже при напряжении σ ₂ (точка С).

Более универсальное представление критерия разрушения приведено на рис. 5.5. Вправо отложена величина приращения длины трещины Δ α, а влево —начальный размер трещины а_г Как и прежде, величина G представлена прямыми линиями, например при напряжении σ ₂ величина G задана линией LF. Из всех точек линии LF реальную ситуацию описывает только точка F, поскольку с самого начала размер трещины равен а₁. При возрастании нагрузки на трещину от нуля до σ ₂ соответствующая ей величина G возрастает от 0 до F. Дальнейшее увеличение напряжения до величины а_{ приводит к увеличению G до точки Н. После этого происходит разрушение. Расширение трещины при напряжении а₁ приводит к изменению G вдоль линии FIK, и, следовательно, G остается большим, чем R.

Если нагрузка на трещину размера а₂ возрастает от нуля до σ ₂, то соответствующее ей значение G увеличивается от 0 до Я (обратите внимание на то, что линии LF и МН параллельны). В точке Η происходит увеличение длины трещины: если напряжение остается равным σ ₂, то скорость выделения энергии изменяется вдоль линии Η Ν и G остается большим, чем R.

В § 5.1 было показано, что в обоих случаях роста трещины при постоянном напряжении и при фиксированных захватах величина G

имеет одно и то же значение. Однако это имеет место только ι начале процесса увеличения длины трещины. В процессе роста трещины это условие не выполняется. Если распространение трещины происходит при постоянном напряжении, то G меняется вдоль прямых линий, как показано на рис. 5.5. Если рост трещины происходит при неподвижных захватах, то напряжение уменьшается. Поскольку то отсюда следует, что величина G увеличивается не пропорциональ-

но а, а медленнее (рис. 5.6). При определенной геометрии образца, если рост трещины происходит при неподвижных захватах, G может даже уменьшиться. Обсуждению этой задачи, а также вытекающих отсюда следствий посвящена гл. VI.

§ 5.3. Сопротивление росту трещины (R-кривая)

До сих пор величина R рассматривалась как не зависящая от длины трещины. Это приблизительно верно для трещин, находящихся в плоском деформированном состоянии. В случае плоского напряженного состояния сопротивление росту трещины, как было показано в экспериментах, изменяется.

Рассмотрим трещину в листе, достаточно тонком для того, чтобы в нем возникло плоское напряженное состояние (см. гл. VII и VIII). Когда образец нагружен до напряжения σ _; , начинается процесс распространения трещины. Однако процесс роста трещины пока стабилен и разрушение еще не наступает. Если напряжение остается равным σ., то трещина распространяется только на небольшое расстояние и останавливается. Для поддержания процесса роста трещины необходимо дальнейшее увеличение напряжения: несмотря на то что трещина стала длиннее, она может выдержать большие напряжения. Процесс одновременного увеличения размера трещины и напряжения может быть продолжен, пока при напряжении а_с не будет достигнут критический размер трещины а_с, при котором возникает неустойчивость, предшествующая разрушению. Этот процесс проиллюстрирован на рис. 5.7.

В начале процесса роста трещины должен выполняться энергетический критерий. При стабильном росте трещины скорость выделения энергии в точности равна сопротивлению росту трещины (если она меньше, то трещина прекращает расти, если больше, то возни-

кает нестабильность, предшествующая разрушению). Скорость выделения энергии G ¢ = π σ ²α ί Ε, и во время роста трещины увеличивается как σ, так и а. Это означает, что G увеличивается не пропорционально а, а быстрее. Так как G ¢ = R, то отсюда следует заключить, что R увеличивается так, как показано графически на рис. 5.8. Пусть трещина размера а. нагружена до напряжения α ι. Если бы трещина росла, то количество выделяемой при этом энергии было бы задано точкой А. Однако эта вели-

чина слишком мала для того, чтобы трещина росла. Напряжение может быть далее увеличено до σ.; скорость выделения энергии при этом будет задана точкой В

Пусть это значение достаточно для роста трещины. Если бы трещина распространялась при постоянном напряжении, то величина G увеличивалась бы по линии ВН. Эта линия лежит ниже ^-кривой, и поэтому при постоянном напряжении трещина расти не может.

Дальнейшее увеличение напряжения до величины σ ₂ приводит к увеличению размера трещины на Аа₂. Величины G и R изменяются вдоль ^-кривой от β к С. Наконец, при напряжении о_с длина трещины становится равной а_с, а величины G и R доходят до точки D. Рост трещины при постоянном напряжении а_с сопровождается увеличением G по линии DF. Эта линия лежит выше ^-кривой. Поскольку G остается большим, чем R, происходит окончательное разрушение в точке D, в которой

Уравнение (5.19), очевидно, представляет собой энергетический критерий для разрушения при плоском напряженном состоянии. Количественная оценка этого критерия разрушения возможна, если будет получено аналитическое выражение для ^-кривой. Попытки вывода этого выражения были сделаны в работах [8—11]. Оценка критерия разрушения проведена в гл. VIII.

Крафт и др. [12] сделали предположение, что ^-кривая инвариантна: она имеет одинаковый вид безотносительно к начальному размеру трещины. Это означает, что условие разрушения для трещин произвольных размеров следует из графического построения, которое выполнено на рис. 5.9, где касательные для различных длин трещин проведены к единственной /^-кривой.

7? -кривая представляет собой энергию, необходимую для роста трещины. В вязком материале эта энергия слагается из работы, необходимой для образования новой зоны пластичности при вершине развивающейся трещины, и работы, необходимой для образования,

роста и слияния микропустот. Наиболее вероятно, что последняя мала по сравнению с энергией, содержащейся в зоне пластичности. Поэтому ^-кривая должна начинаться в нулевой точке, как показано на рис. 5.9: при нулевых напряжениях размер зоны пластичности равен нулю. Это также означает, что при любом напряжении, отличном от нуля, выполняется энергетический критерий (не считая работы образования пустот). Однако трещина не растет, поскольку напряжения и пластические деформации все еще недостаточны. Энергетический критерий является критерием необходимым, но недостаточным.

Материал при вершине трещины не будет готов к расцеплению, пока напряжения и деформации не станут достаточно велики, чтобы стало возможно образование и слияние пустот. К моменту, когда возникает такая ситуация, образуется довольно большая зона пластичности. Трещина может расти только в том случае, если в процессе ее роста выделяется достаточно энергии, чтобы совершить работу по образованию зоны пластичности при новой вершине трещины. Трещина не может расти, если не удовлетворено это энергетическое условие; она должна расти, если это условие удовлетворено.

Легко видеть, что все линии роста трещин пересекаются в точке В (рис. 5.9). Эта точка является общей для трещин с размерами а_л и а₂, поэтому

(5.20)

Стабильный рост трещины начинается при определенном значении G, а именно при G_; , заданном уравнением (5.20). При G, равном G., рост трещины происходит от точки В до точки Ci или С₂, где G? = R. Это первое отдельное расширение трещины называется хлопком, потому что представляет собой внезапное метастабильное расширение трещины, которое часто сопровождается звучным щелчком. После хлопка происходит непрерывный стабильный медленный рост трещины, пока в точке D_± или D₂ не последует разрушение.

Для двух рассматриваемых трещин значения G равны соответственно G_lcl и G_ic2. Это означает, что критическая скорость выделения энергии для плоского напряженного состояния G_ic не является постоянной величиной и, поскольку К²и = EG_ic, отсюда величина Ki_c также непостоянна (индекс 1 используется здесь для обозначения плоского напряженного состояния в трещине типа I, чтобы отличать Ки и G_lc от значений К\с и G\_c при плоской деформации). В отличие от случая плоской деформации, когда G\_c и К\с в определенных пределах являются константами материала, величины G_ic и Ki_c зависят от размера трещины и для больших трещин имеют большие значения.

В § 5.1 было отмечено, что с помощью соотношения К²1 = EG_i к величине G можно применить коррекцию на конечность размеров. Используя при этом коррекцию Ирвина [3] (см. гл. III), получим

(5.21)

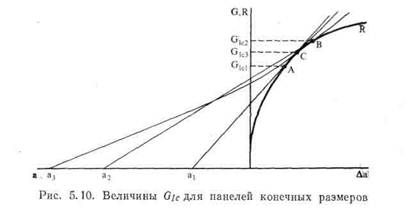
Уравнение (5.21) означает, что линии G —не прямые, а имеют положительную кривизну, как показано на рис. 5.10. Для маленькой трещины коррекцией на конечность размеров можно пренебречь и считать линию G приблизительно прямой. По мере удлинения трещин увеличивается и кривизна. В результате значение G_lc сначала уве-

 

личивается от G_ici до G_ic2, а затем вновь уменьшается до G_lcS, как показано на рис. 5.11.

Были предложены различные формы ^-кривых (см. [13]), некоторые из которых приведены на рис. 5.12. Горизонтальная часть

этих кривых используется для объяснения явления хлопка. Однако скорее всего ^-кривые начинаются в нулевой точке. Рис. 5.9 показывает, что хлопок может произойти и в том случае, если /^-кривая начинается в нулевой точке. Форма R- кривой зависит от толщины пластины. Для толстых пластин, находящихся в плоском деформированном состоянии, они представляют собой пря-

 

мую горизонтальную линию. Для тонких пластин, находящихся в плоском напряженном состоянии, /^-кривая имеет ступеньку и возрастающий участок. Переходной зоне пластин промежуточной толщины соответствует ^-кривая, форма которой является чем-то средним между этими двумя крайними случаями.

Теория ^-кривых до конца еще не разработана. В гл. VIII приведена дальнейшая информация о ^-кривых и процессе разрушения при плоском напряженном состоянии. Здесь же представлены R- кривые, полученные экспериментально.