Теоретическая механика
(дополнительные главы)
Задания для студентов заочно-сокращенной формы обучения
Методика выбора варианта на выполнение контрольных работ
Каждая задача имеет 30 вариантов. Номер варианта студент определяет самостоятельно по двум последним цифрам своего шифра с помощью таблицы 1.
Таблица 1.
|
| Последняя цифра шифра
|
| предпоследняя цифра шифра
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача Д3.
Свободные колебания материальной точки
При решении задач на прямолинейные колебания материальной точки рекомендуется следующий алгоритм:
1) расчетная схема (по возможности упрощается физическая схема): изображается исследуемая материальная точка в выбранной системе координат в текущий момент времени;
2) указываются силы действующие на материальную точку;
3) составляется дифференциальное уравнение движения материальной точки;
4) решается полученное уравнение и находятся неизвестные
При решении задач, связанных с исследованием прямолинейных колебаний материальной точки, следует учитывать некоторые особенности составления расчетной схемы.
Если груз, грузы (материальная точка) прикреплены к нескольким пружинам, то на расчетной схеме рекомендуется изображать одну эквивалентную пружину и указать длину пружины в свободном, ненапряженном состоянии.
На расчетной схеме рекомендуется изображать три точки: начало координат рекомендуется выбирать в положении статического равновесия колеблющейся материальной точки (это может быть один груз или система грузов), начальное положение (определяется условием задачи) и текущее положение (любое направление на положительном направлении оси).
Пример 1
 На платформе весом P, подрессоренной пружиной жесткостью c, покоится груз весом G. В некоторый момент времени груз толчком сбрасывается с платформы. Определите уравнение последующих колебаний платформы.
На платформе весом P, подрессоренной пружиной жесткостью c, покоится груз весом G. В некоторый момент времени груз толчком сбрасывается с платформы. Определите уравнение последующих колебаний платформы.
1. Составляем расчётную схему.
Объект исследования — платформа весом P совершает прямолинейные колебания вдоль вертикальной оси, следовательно её можно представить как материальную точку. Изобразим на расчётной схеме вертикальную ось x, направленную вниз, покажем на ней положение недеформированной пружины О1 (рис. 2, а). Начало координат О выбираем в положении статического равновесия (рис. 2, б) нашего объекта исследования. Условия статичекого равновесия записываются в виде:
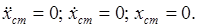
(1)
В начальный момент времени пружина была сдеформирована под статическим действием платформы и груза, на рис. 2, в покажем начальное положение точки — М0, эта точка также соответствует статическому равновесию платформы с грузом. Введём обозначения: fст — статическая деформация пружины; fст2 — статическая деформация пружины под действием платформы и груза; x 0 — начальная координата точки; x — координата точки в произвольном положении. Произвольное положение объекта исследования покажем на рис. 2, г. Отметим характерные точки О1, О, М, М0 на расчётной схеме (рис. 2, д).
Начальные условия колебаний запишутся в виде
 (2)
(2)
2. На материальную точку действуют силы:
 — сила тяжести;
— сила тяжести;
 — сила упругости пружины (определяется как произведение жёсткости пружины на её полную деформацию, полную деформацию пружины определяем на расчётной схеме — это расстояние между концом недеформированной пружины (рис. 2, а) и произвольным положением точки (рис. 2, г)).
— сила упругости пружины (определяется как произведение жёсткости пружины на её полную деформацию, полную деформацию пружины определяем на расчётной схеме — это расстояние между концом недеформированной пружины (рис. 2, а) и произвольным положением точки (рис. 2, г)).
3. Составляем дифференциальное уравнение движения точки в форме второго закона Ньютона.
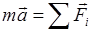
или в проекции на ось x:
 . (3)
. (3)
Для определения статической деформации в дифференциальное уравнение (3) подставим условия статического равновесия (1):
 , откуда
, откуда
 . (4)
. (4)
Подставив fст в дифференциальное уравнение и проведя несложные преобразования, получим
 , (5)
, (5)
где  — круговая частота свободных колебаний.
— круговая частота свободных колебаний.
4. Решаем дифференциальное уравнение.
Дифференциальное уравнение (5) описывает случай свободных незатухающих колебаний и его решение ищется в виде
 . (6)
. (6)
Для определения постоянных интегрирования C 1 и C 2 подставим в (6) начальные условия (2), для чего предварительно найдём первую производную от уравнения движения:
 ;
;
 ;
;
 .
.
Откуда выразим
 (7)
(7)
Вариант 1
 2. На платформе весом 40 Н, подрессоренной пружиной жесткостью 200 Н/см, покоится груз весом 64 Н. В некоторый момент времени груз толчком сбрасывается с платформы. Определите уравнение последующих колебаний платформы, считая ось x проведенной вертикально вниз из положения статического равновесия платформы на пружине.
2. На платформе весом 40 Н, подрессоренной пружиной жесткостью 200 Н/см, покоится груз весом 64 Н. В некоторый момент времени груз толчком сбрасывается с платформы. Определите уравнение последующих колебаний платформы, считая ось x проведенной вертикально вниз из положения статического равновесия платформы на пружине.
|
Вариант 2
 2. Груз весом 490 Н падает без начальной скорости с высоты h = 0, 1 м на упругую невесомую балку жесткостью 200 Н/см. Найдите уравнение колебаний груза, считая ось x проведенной вертикально вниз из положения статического равновесия груза на балке. 2. Груз весом 490 Н падает без начальной скорости с высоты h = 0, 1 м на упругую невесомую балку жесткостью 200 Н/см. Найдите уравнение колебаний груза, считая ось x проведенной вертикально вниз из положения статического равновесия груза на балке.
|
Вариант 3
 2. Пружину жесткостью 2 Н/см растянули относительно ее свободного состояния на 2, 5 см, подвесили груз весом 12 Н и сообщили ему скорость 1, 5 см/с, направленную вертикально вниз. Определите уравнение последующих колебаний, считая ось x проведенной вертикально вниз из центра колебаний. 2. Пружину жесткостью 2 Н/см растянули относительно ее свободного состояния на 2, 5 см, подвесили груз весом 12 Н и сообщили ему скорость 1, 5 см/с, направленную вертикально вниз. Определите уравнение последующих колебаний, считая ось x проведенной вертикально вниз из центра колебаний.
|
Вариант 4
 2. Груз весом 50 Н, прикрепленный к недеформированной пружине жесткостью 5 Н/см, отвели на 4 см вниз по гладкой наклонной плоскости и отпустили, дав импульс вверх. Определите уравнение последующих колебаний, если известно, что максимальное удлинение пружины при колебаниях равно 8 см. 2. Груз весом 50 Н, прикрепленный к недеформированной пружине жесткостью 5 Н/см, отвели на 4 см вниз по гладкой наклонной плоскости и отпустили, дав импульс вверх. Определите уравнение последующих колебаний, если известно, что максимальное удлинение пружины при колебаниях равно 8 см.
|
Вариант 5
 2. Груз весом 98 Н удерживается на гладкой наклонной плоскости пружиной жесткостью 10 Н/см. Найдите уравнение колебаний груза, отпущенного без начальной скорости в момент, когда пружина была растянута относительно ее свободного состояния на 9, 8 см. 2. Груз весом 98 Н удерживается на гладкой наклонной плоскости пружиной жесткостью 10 Н/см. Найдите уравнение колебаний груза, отпущенного без начальной скорости в момент, когда пружина была растянута относительно ее свободного состояния на 9, 8 см.
|
Вариант 6
2. Груз под действием пружины совершает колебания на гладкой горизонтальной плоскости с угловой частотой k = 10 с-1. Запишите уравнение колебаний, отсчитывая  координату x от центра колебаний и приняв следующие начальные условия: х 0 = 5 см, V 0 = 50 см/с. координату x от центра колебаний и приняв следующие начальные условия: х 0 = 5 см, V 0 = 50 см/с.
|
Вариант 7
2  . Пружина жесткостью 4 Н/см в начальный момент была сжата относительно ее свободного состояния на 1 см и груз отпущен без начальной скорости. Определите уравнение последующих колебаний груза, если начало оси x соответствует положению статического равновесия груза. Плоскость считать гладкой, груз весит 12 Н. . Пружина жесткостью 4 Н/см в начальный момент была сжата относительно ее свободного состояния на 1 см и груз отпущен без начальной скорости. Определите уравнение последующих колебаний груза, если начало оси x соответствует положению статического равновесия груза. Плоскость считать гладкой, груз весит 12 Н.
|
Вариант 8
 2. Найдите уравнение колебаний груза весом 196 Н. Пружина жесткостью 20 Н/см в начальный момент времени быласжата относительно ее свободного состояния на 4, 9см и груз отпущенбез начальной скорости. 2. Найдите уравнение колебаний груза весом 196 Н. Пружина жесткостью 20 Н/см в начальный момент времени быласжата относительно ее свободного состояния на 4, 9см и груз отпущенбез начальной скорости.
|
Вариант 9
 2. Груз весом 3, 92 Н удерживается на гладкой наклонной плоскости пружиной жесткостью 0, 9 Н/см. Найдите уравнение колебаний груза, если в начальный момент времени пружину растянули на 4, 6 см и отпустили груз без начальной скорости. 2. Груз весом 3, 92 Н удерживается на гладкой наклонной плоскости пружиной жесткостью 0, 9 Н/см. Найдите уравнение колебаний груза, если в начальный момент времени пружину растянули на 4, 6 см и отпустили груз без начальной скорости.
|
Вариант 10
 2. Найдите уравнение колебаний груза на гладкой горизонтальной плоскости, если известны собственная частота k = 14 с-1 и начальные условия x 0 = 0 см, 2. Найдите уравнение колебаний груза на гладкой горизонтальной плоскости, если известны собственная частота k = 14 с-1 и начальные условия x 0 = 0 см,  см/с. Координата x отсчитывается от центра колебаний. см/с. Координата x отсчитывается от центра колебаний.
|
Вариант 11
 2. Груз весом 800 Н падаетиз состояния покоя с высоты h = 0, 1 м на невесомую платформу, укрепленную на упругом фундаменте жесткостью 40 Н/см. Найдите уравнение движении груза, предполагая, что после встречи с платформой груз не отделяется от нее. 2. Груз весом 800 Н падаетиз состояния покоя с высоты h = 0, 1 м на невесомую платформу, укрепленную на упругом фундаменте жесткостью 40 Н/см. Найдите уравнение движении груза, предполагая, что после встречи с платформой груз не отделяется от нее.
|
Вариант 12
 2. Груз весом 40 Н подвесили к вертикальной недеформированной пружине и отпустили, сообщив скорость 70 см/с вниз. Известно, что длина недеформированной пружины 40 см, а при равновесии груза на пружине ее длина 45 см. Определите уравнение движения груза, вдоль оси x. 2. Груз весом 40 Н подвесили к вертикальной недеформированной пружине и отпустили, сообщив скорость 70 см/с вниз. Известно, что длина недеформированной пружины 40 см, а при равновесии груза на пружине ее длина 45 см. Определите уравнение движения груза, вдоль оси x.
|
Вариант 13
 2. К концу сжатой на2, 55 см вертикальной пружины, коэффициент жесткости которой 2 Н/см, подвешен грузвесом 4, 9 Н, ему сообщена скорость 40 см/с, направленная вертикально вниз. Определите уравнение движения груза, выбрав начало координат в положении его статического равновесия и направив ось вниз. 2. К концу сжатой на2, 55 см вертикальной пружины, коэффициент жесткости которой 2 Н/см, подвешен грузвесом 4, 9 Н, ему сообщена скорость 40 см/с, направленная вертикально вниз. Определите уравнение движения груза, выбрав начало координат в положении его статического равновесия и направив ось вниз.
|
Вариант 14
 2. Пружину с коэффициентом жесткости с = 10 Н/см сжалина 5 см, прикрепили к ней груз весом 98 Н и сообщили ему скорость 20 см/с по гладкой наклонной плоскости вниз. Определите уравнение движения груза относительно положения его статического равновесия. 2. Пружину с коэффициентом жесткости с = 10 Н/см сжалина 5 см, прикрепили к ней груз весом 98 Н и сообщили ему скорость 20 см/с по гладкой наклонной плоскости вниз. Определите уравнение движения груза относительно положения его статического равновесия.
|
Вариант 15
 2. Найдите уравнение колебаний груза весом 3, 92 Н, подвешенного на пружине жесткостью 1, 6 Н/см, если в начальный момент времени пружина была растянута относительно ее свободного состояния на величину 5 см и грузу сообщена скорость 80 см/с, направленная по вертикали вверх. Движение груза отнести к оси x, проведенной вертикально вниз из положения статического равновесия груза на пружине. 2. Найдите уравнение колебаний груза весом 3, 92 Н, подвешенного на пружине жесткостью 1, 6 Н/см, если в начальный момент времени пружина была растянута относительно ее свободного состояния на величину 5 см и грузу сообщена скорость 80 см/с, направленная по вертикали вверх. Движение груза отнести к оси x, проведенной вертикально вниз из положения статического равновесия груза на пружине.
|
Вариант 16
 2. Грузы весом 2 Н и 5 Н подвешены на пружине жесткостью 10 Н/см и находятся в состоянии покоя. Определите уравнение колебаний меньшего груза после пережигания связывающей их нити, считая, что ось x проведена вниз из положения статического равновесия меньшего груза на пружине. 2. Грузы весом 2 Н и 5 Н подвешены на пружине жесткостью 10 Н/см и находятся в состоянии покоя. Определите уравнение колебаний меньшего груза после пережигания связывающей их нити, считая, что ось x проведена вниз из положения статического равновесия меньшего груза на пружине.
|
 Вариант 17
2. На вертикально расположенной пружине подвешены два равных груза, в результате чего она получила статическое удлинение λ = 10 см. Затем один из грузов оборвался. Найдите уравнение движения оставшегося груза, пренебрегая массой пружины. Вариант 17
2. На вертикально расположенной пружине подвешены два равных груза, в результате чего она получила статическое удлинение λ = 10 см. Затем один из грузов оборвался. Найдите уравнение движения оставшегося груза, пренебрегая массой пружины.
|
Вариант 18
 2. Определите уравнение колебаний груза весом P = 40 Н, считая, что начало оси x соответствует положению статического равновесия груза. Пружина жесткостью 8 Н/см в начальный момент была сжата относительно ее свободного состояния на 1, 5 см и грузу сообщена скорость V 0 = 12 см/с, направленная вниз по наклонной плоскости. 2. Определите уравнение колебаний груза весом P = 40 Н, считая, что начало оси x соответствует положению статического равновесия груза. Пружина жесткостью 8 Н/см в начальный момент была сжата относительно ее свободного состояния на 1, 5 см и грузу сообщена скорость V 0 = 12 см/с, направленная вниз по наклонной плоскости.
|
Вариант 19
 2. Груз весом 1, 96 Н удерживается на гладкой наклонной поверхности пружиной жесткостью 0, 2 Н/см. Найдите уравнение колебаний груза, если в начальный момент пружину растянули на 4, 9 см и грузу сообщили скорость 60 см/с вниз вдоль плоскости. 2. Груз весом 1, 96 Н удерживается на гладкой наклонной поверхности пружиной жесткостью 0, 2 Н/см. Найдите уравнение колебаний груза, если в начальный момент пружину растянули на 4, 9 см и грузу сообщили скорость 60 см/с вниз вдоль плоскости.
|
 Вариант 20
2. При статическом равновесии груза, принятом за начало отсчета координаты x, пружина сжата на 5 см. Определите уравнение колебаний груза на пружине, если в начальный момент времени она была растянута относительно своего свободного состояния на 2, 5 см и груз отпущен без начальной скорости. Вариант 20
2. При статическом равновесии груза, принятом за начало отсчета координаты x, пружина сжата на 5 см. Определите уравнение колебаний груза на пружине, если в начальный момент времени она была растянута относительно своего свободного состояния на 2, 5 см и груз отпущен без начальной скорости.
|
Вариант 21
 2. Груз весом 490 Н падает без начальной скорости с высоты h = 0, 1 м на упругую невесомую балку жесткостью 200 Н/см. Найдите уравнение колебаний груза, считая ось x проведенной вертикально вниз из положения статического равновесия груза на балке. 2. Груз весом 490 Н падает без начальной скорости с высоты h = 0, 1 м на упругую невесомую балку жесткостью 200 Н/см. Найдите уравнение колебаний груза, считая ось x проведенной вертикально вниз из положения статического равновесия груза на балке.
|
Вариант 22
 2. Пружину жесткостью 2 Н/см растянули относительно ее свободного состояния на 2, 5 см, подвесили груз весом 12 Н и сообщили ему скорость 1, 5 см/с, направленную вертикально вниз. Определите уравнение последующих колебаний, считая ось x проведенной вертикально вниз из центра колебаний. 2. Пружину жесткостью 2 Н/см растянули относительно ее свободного состояния на 2, 5 см, подвесили груз весом 12 Н и сообщили ему скорость 1, 5 см/с, направленную вертикально вниз. Определите уравнение последующих колебаний, считая ось x проведенной вертикально вниз из центра колебаний.
|
Вариант 23
 2. Груз весом 50 Н, прикрепленный к недеформированной пружине жесткостью 5 Н/см, отвели на 4 см вниз по гладкой наклонной плоскости и отпустили, дав импульс вверх. Определите уравнение последующих колебаний, если известно, что максимальное удлинение пружины при колебаниях равно 8 см. 2. Груз весом 50 Н, прикрепленный к недеформированной пружине жесткостью 5 Н/см, отвели на 4 см вниз по гладкой наклонной плоскости и отпустили, дав импульс вверх. Определите уравнение последующих колебаний, если известно, что максимальное удлинение пружины при колебаниях равно 8 см.
|
Вариант 24
 2. Груз весом 98 Н удерживается на гладкой наклонной плоскости пружиной жесткостью 10 Н/см. Найдите уравнение колебаний груза, отпущенного без начальной скорости в момент, когда пружина была растянута относительно ее свободного состояния на 9, 8 см. 2. Груз весом 98 Н удерживается на гладкой наклонной плоскости пружиной жесткостью 10 Н/см. Найдите уравнение колебаний груза, отпущенного без начальной скорости в момент, когда пружина была растянута относительно ее свободного состояния на 9, 8 см.
|
Вариант 25
2. Груз под действием пружины совершает колебания на гладкой горизонтальной плоскости с угловой частотой k = 10 с-1. Запишите уравнение колебаний, отсчитывая  координату x от центра колебаний и приняв следующие начальные условия: х 0 = 5 см, V 0 = 50 см/с. координату x от центра колебаний и приняв следующие начальные условия: х 0 = 5 см, V 0 = 50 см/с.
|
Вариант 26
2  . Пружина жесткостью 4 Н/см в начальный момент была сжата относительно ее свободного состояния на 1 см и груз отпущен без начальной скорости. Определите уравнение последующих колебаний груза, если начало оси x соответствует положению статического равновесия груза. Плоскость считать гладкой, груз весит 12 Н. . Пружина жесткостью 4 Н/см в начальный момент была сжата относительно ее свободного состояния на 1 см и груз отпущен без начальной скорости. Определите уравнение последующих колебаний груза, если начало оси x соответствует положению статического равновесия груза. Плоскость считать гладкой, груз весит 12 Н.
|
Вариант 27
 2. Найдите уравнение колебаний груза весом 196 Н. Пружина жесткостью 20 Н/см в начальный момент времени быласжата относительно ее свободного состояния на 4, 9см и груз отпущенбез начальной скорости. 2. Найдите уравнение колебаний груза весом 196 Н. Пружина жесткостью 20 Н/см в начальный момент времени быласжата относительно ее свободного состояния на 4, 9см и груз отпущенбез начальной скорости.
|
Вариант 28
 2. Груз весом 3, 92 Н удерживается на гладкой наклонной плоскости пружиной жесткостью 0, 9 Н/см. Найдите уравнение колебаний груза, если в начальный момент времени пружину растянули на 4, 6 см и отпустили груз без начальной скорости. 2. Груз весом 3, 92 Н удерживается на гладкой наклонной плоскости пружиной жесткостью 0, 9 Н/см. Найдите уравнение колебаний груза, если в начальный момент времени пружину растянули на 4, 6 см и отпустили груз без начальной скорости.
|
Вариант 29
 2. Найдите уравнение колебаний груза на гладкой горизонтальной плоскости, если известны собственная частота k = 14 с-1 и начальные условия x 0 = 0 см, 2. Найдите уравнение колебаний груза на гладкой горизонтальной плоскости, если известны собственная частота k = 14 с-1 и начальные условия x 0 = 0 см,  см/с. Координата x отсчитывается от центра колебаний. см/с. Координата x отсчитывается от центра колебаний.
|
Вариант 30
 2. Груз весом 800 Н падаетиз состояния покоя с высоты h = 0, 1 м на невесомую платформу, укрепленную на упругом фундаменте жесткостью 40 Н/см. Найдите уравнение движении груза, предполагая, что после встречи с платформой груз не отделяется от нее. 2. Груз весом 800 Н падаетиз состояния покоя с высоты h = 0, 1 м на невесомую платформу, укрепленную на упругом фундаменте жесткостью 40 Н/см. Найдите уравнение движении груза, предполагая, что после встречи с платформой груз не отделяется от нее.
|

 На платформе весом P, подрессоренной пружиной жесткостью c, покоится груз весом G. В некоторый момент времени груз толчком сбрасывается с платформы. Определите уравнение последующих колебаний платформы.
На платформе весом P, подрессоренной пружиной жесткостью c, покоится груз весом G. В некоторый момент времени груз толчком сбрасывается с платформы. Определите уравнение последующих колебаний платформы.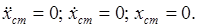

 (2)
(2) — сила тяжести;
— сила тяжести; — сила упругости пружины (определяется как произведение жёсткости пружины на её полную деформацию, полную деформацию пружины определяем на расчётной схеме — это расстояние между концом недеформированной пружины (рис. 2, а) и произвольным положением точки (рис. 2, г)).
— сила упругости пружины (определяется как произведение жёсткости пружины на её полную деформацию, полную деформацию пружины определяем на расчётной схеме — это расстояние между концом недеформированной пружины (рис. 2, а) и произвольным положением точки (рис. 2, г)).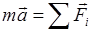
 . (3)
. (3) , откуда
, откуда . (4)
. (4) , (5)
, (5) — круговая частота свободных колебаний.
— круговая частота свободных колебаний. . (6)
. (6) ;
; ;
; .
. (7)
(7) 2. На платформе весом 40 Н, подрессоренной пружиной жесткостью 200 Н/см, покоится груз весом 64 Н. В некоторый момент времени груз толчком сбрасывается с платформы. Определите уравнение последующих колебаний платформы, считая ось x проведенной вертикально вниз из положения статического равновесия платформы на пружине.
2. На платформе весом 40 Н, подрессоренной пружиной жесткостью 200 Н/см, покоится груз весом 64 Н. В некоторый момент времени груз толчком сбрасывается с платформы. Определите уравнение последующих колебаний платформы, считая ось x проведенной вертикально вниз из положения статического равновесия платформы на пружине.
 2. Груз весом 490 Н падает без начальной скорости с высоты h = 0, 1 м на упругую невесомую балку жесткостью 200 Н/см. Найдите уравнение колебаний груза, считая ось x проведенной вертикально вниз из положения статического равновесия груза на балке.
2. Груз весом 490 Н падает без начальной скорости с высоты h = 0, 1 м на упругую невесомую балку жесткостью 200 Н/см. Найдите уравнение колебаний груза, считая ось x проведенной вертикально вниз из положения статического равновесия груза на балке.
 2. Пружину жесткостью 2 Н/см растянули относительно ее свободного состояния на 2, 5 см, подвесили груз весом 12 Н и сообщили ему скорость 1, 5 см/с, направленную вертикально вниз. Определите уравнение последующих колебаний, считая ось x проведенной вертикально вниз из центра колебаний.
2. Пружину жесткостью 2 Н/см растянули относительно ее свободного состояния на 2, 5 см, подвесили груз весом 12 Н и сообщили ему скорость 1, 5 см/с, направленную вертикально вниз. Определите уравнение последующих колебаний, считая ось x проведенной вертикально вниз из центра колебаний.
 2. Груз весом 50 Н, прикрепленный к недеформированной пружине жесткостью 5 Н/см, отвели на 4 см вниз по гладкой наклонной плоскости и отпустили, дав импульс вверх. Определите уравнение последующих колебаний, если известно, что максимальное удлинение пружины при колебаниях равно 8 см.
2. Груз весом 50 Н, прикрепленный к недеформированной пружине жесткостью 5 Н/см, отвели на 4 см вниз по гладкой наклонной плоскости и отпустили, дав импульс вверх. Определите уравнение последующих колебаний, если известно, что максимальное удлинение пружины при колебаниях равно 8 см.
 2. Груз весом 98 Н удерживается на гладкой наклонной плоскости пружиной жесткостью 10 Н/см. Найдите уравнение колебаний груза, отпущенного без начальной скорости в момент, когда пружина была растянута относительно ее свободного состояния на 9, 8 см.
2. Груз весом 98 Н удерживается на гладкой наклонной плоскости пружиной жесткостью 10 Н/см. Найдите уравнение колебаний груза, отпущенного без начальной скорости в момент, когда пружина была растянута относительно ее свободного состояния на 9, 8 см.
 координату x от центра колебаний и приняв следующие начальные условия: х 0 = 5 см, V 0 = 50 см/с.
координату x от центра колебаний и приняв следующие начальные условия: х 0 = 5 см, V 0 = 50 см/с.
 . Пружина жесткостью 4 Н/см в начальный момент была сжата относительно ее свободного состояния на 1 см и груз отпущен без начальной скорости. Определите уравнение последующих колебаний груза, если начало оси x соответствует положению статического равновесия груза. Плоскость считать гладкой, груз весит 12 Н.
. Пружина жесткостью 4 Н/см в начальный момент была сжата относительно ее свободного состояния на 1 см и груз отпущен без начальной скорости. Определите уравнение последующих колебаний груза, если начало оси x соответствует положению статического равновесия груза. Плоскость считать гладкой, груз весит 12 Н.
 2. Найдите уравнение колебаний груза весом 196 Н. Пружина жесткостью 20 Н/см в начальный момент времени быласжата относительно ее свободного состояния на 4, 9см и груз отпущенбез начальной скорости.
2. Найдите уравнение колебаний груза весом 196 Н. Пружина жесткостью 20 Н/см в начальный момент времени быласжата относительно ее свободного состояния на 4, 9см и груз отпущенбез начальной скорости.
 2. Груз весом 3, 92 Н удерживается на гладкой наклонной плоскости пружиной жесткостью 0, 9 Н/см. Найдите уравнение колебаний груза, если в начальный момент времени пружину растянули на 4, 6 см и отпустили груз без начальной скорости.
2. Груз весом 3, 92 Н удерживается на гладкой наклонной плоскости пружиной жесткостью 0, 9 Н/см. Найдите уравнение колебаний груза, если в начальный момент времени пружину растянули на 4, 6 см и отпустили груз без начальной скорости.
 2. Найдите уравнение колебаний груза на гладкой горизонтальной плоскости, если известны собственная частота k = 14 с-1 и начальные условия x 0 = 0 см,
2. Найдите уравнение колебаний груза на гладкой горизонтальной плоскости, если известны собственная частота k = 14 с-1 и начальные условия x 0 = 0 см,  см/с. Координата x отсчитывается от центра колебаний.
см/с. Координата x отсчитывается от центра колебаний.
 2. Груз весом 800 Н падаетиз состояния покоя с высоты h = 0, 1 м на невесомую платформу, укрепленную на упругом фундаменте жесткостью 40 Н/см. Найдите уравнение движении груза, предполагая, что после встречи с платформой груз не отделяется от нее.
2. Груз весом 800 Н падаетиз состояния покоя с высоты h = 0, 1 м на невесомую платформу, укрепленную на упругом фундаменте жесткостью 40 Н/см. Найдите уравнение движении груза, предполагая, что после встречи с платформой груз не отделяется от нее.
 2. Груз весом 40 Н подвесили к вертикальной недеформированной пружине и отпустили, сообщив скорость 70 см/с вниз. Известно, что длина недеформированной пружины 40 см, а при равновесии груза на пружине ее длина 45 см. Определите уравнение движения груза, вдоль оси x.
2. Груз весом 40 Н подвесили к вертикальной недеформированной пружине и отпустили, сообщив скорость 70 см/с вниз. Известно, что длина недеформированной пружины 40 см, а при равновесии груза на пружине ее длина 45 см. Определите уравнение движения груза, вдоль оси x.
 2. К концу сжатой на2, 55 см вертикальной пружины, коэффициент жесткости которой 2 Н/см, подвешен грузвесом 4, 9 Н, ему сообщена скорость 40 см/с, направленная вертикально вниз. Определите уравнение движения груза, выбрав начало координат в положении его статического равновесия и направив ось вниз.
2. К концу сжатой на2, 55 см вертикальной пружины, коэффициент жесткости которой 2 Н/см, подвешен грузвесом 4, 9 Н, ему сообщена скорость 40 см/с, направленная вертикально вниз. Определите уравнение движения груза, выбрав начало координат в положении его статического равновесия и направив ось вниз.
 2. Пружину с коэффициентом жесткости с = 10 Н/см сжалина 5 см, прикрепили к ней груз весом 98 Н и сообщили ему скорость 20 см/с по гладкой наклонной плоскости вниз. Определите уравнение движения груза относительно положения его статического равновесия.
2. Пружину с коэффициентом жесткости с = 10 Н/см сжалина 5 см, прикрепили к ней груз весом 98 Н и сообщили ему скорость 20 см/с по гладкой наклонной плоскости вниз. Определите уравнение движения груза относительно положения его статического равновесия.
 2. Найдите уравнение колебаний груза весом 3, 92 Н, подвешенного на пружине жесткостью 1, 6 Н/см, если в начальный момент времени пружина была растянута относительно ее свободного состояния на величину 5 см и грузу сообщена скорость 80 см/с, направленная по вертикали вверх. Движение груза отнести к оси x, проведенной вертикально вниз из положения статического равновесия груза на пружине.
2. Найдите уравнение колебаний груза весом 3, 92 Н, подвешенного на пружине жесткостью 1, 6 Н/см, если в начальный момент времени пружина была растянута относительно ее свободного состояния на величину 5 см и грузу сообщена скорость 80 см/с, направленная по вертикали вверх. Движение груза отнести к оси x, проведенной вертикально вниз из положения статического равновесия груза на пружине.
 2. Грузы весом 2 Н и 5 Н подвешены на пружине жесткостью 10 Н/см и находятся в состоянии покоя. Определите уравнение колебаний меньшего груза после пережигания связывающей их нити, считая, что ось x проведена вниз из положения статического равновесия меньшего груза на пружине.
2. Грузы весом 2 Н и 5 Н подвешены на пружине жесткостью 10 Н/см и находятся в состоянии покоя. Определите уравнение колебаний меньшего груза после пережигания связывающей их нити, считая, что ось x проведена вниз из положения статического равновесия меньшего груза на пружине.
 Вариант 17
2. На вертикально расположенной пружине подвешены два равных груза, в результате чего она получила статическое удлинение λ = 10 см. Затем один из грузов оборвался. Найдите уравнение движения оставшегося груза, пренебрегая массой пружины.
Вариант 17
2. На вертикально расположенной пружине подвешены два равных груза, в результате чего она получила статическое удлинение λ = 10 см. Затем один из грузов оборвался. Найдите уравнение движения оставшегося груза, пренебрегая массой пружины.
 2. Определите уравнение колебаний груза весом P = 40 Н, считая, что начало оси x соответствует положению статического равновесия груза. Пружина жесткостью 8 Н/см в начальный момент была сжата относительно ее свободного состояния на 1, 5 см и грузу сообщена скорость V 0 = 12 см/с, направленная вниз по наклонной плоскости.
2. Определите уравнение колебаний груза весом P = 40 Н, считая, что начало оси x соответствует положению статического равновесия груза. Пружина жесткостью 8 Н/см в начальный момент была сжата относительно ее свободного состояния на 1, 5 см и грузу сообщена скорость V 0 = 12 см/с, направленная вниз по наклонной плоскости.
 2. Груз весом 1, 96 Н удерживается на гладкой наклонной поверхности пружиной жесткостью 0, 2 Н/см. Найдите уравнение колебаний груза, если в начальный момент пружину растянули на 4, 9 см и грузу сообщили скорость 60 см/с вниз вдоль плоскости.
2. Груз весом 1, 96 Н удерживается на гладкой наклонной поверхности пружиной жесткостью 0, 2 Н/см. Найдите уравнение колебаний груза, если в начальный момент пружину растянули на 4, 9 см и грузу сообщили скорость 60 см/с вниз вдоль плоскости.
 Вариант 20
2. При статическом равновесии груза, принятом за начало отсчета координаты x, пружина сжата на 5 см. Определите уравнение колебаний груза на пружине, если в начальный момент времени она была растянута относительно своего свободного состояния на 2, 5 см и груз отпущен без начальной скорости.
Вариант 20
2. При статическом равновесии груза, принятом за начало отсчета координаты x, пружина сжата на 5 см. Определите уравнение колебаний груза на пружине, если в начальный момент времени она была растянута относительно своего свободного состояния на 2, 5 см и груз отпущен без начальной скорости.
 2. Найдите уравнение колебаний груза весом 196 Н. Пружина жесткостью 20 Н/см в начальный момент времени быласжата относительно ее свободного состояния на 4, 9см и груз отпущенбез начальной скорости.
2. Найдите уравнение колебаний груза весом 196 Н. Пружина жесткостью 20 Н/см в начальный момент времени быласжата относительно ее свободного состояния на 4, 9см и груз отпущенбез начальной скорости.
 см/с. Координата x отсчитывается от центра колебаний.
см/с. Координата x отсчитывается от центра колебаний.



