Упражнения
25. (12/ 6) ® (12/3) 26. (15/ 6) ® (15/3) 27. Определить истинность А: А ® (4 – нечетное число)=1 28. Определить истинность А: (2 – четное число) ® А=0
Эквивалентность (равнозначность). Обозначение: Ø в естественном языке соответствует обороту речи тогда и только тогда; Ø в алгебре высказываний обозначение Û, ~; Ø в языках программирования обозначение Eqv. Эквивалентность – это логическая операция, которая каждым двум простым высказываниям ставит в соответствие составное высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны. Таблица истинности
Свойства операции: A «B = B «A
A «0 = A «1 = А А«А=А Примеры: 29. 2*2=5 тогда и только тогда, когда белые медведи заживут в Африке. 30. Четырехугольник является параллелограммом, тогда и только тогда, когда его диагонали в точке пересечения делятся пополам. 31. Для того, чтобы число было четным, необходимо и достаточно, чтобы оно делилось на 2 без остатка. Формула (A ®) & (B ® A)
Упражнения. 32. (12/ 6) «(12/3) 33. (15/ 6) «(15/3) 34. Определить истинность А: А «(22=5)=1 35. Определить истинность А: А «(22=4)=0 Исключающее или (иначе называется разделительной дизъюнкцией (это значит “один или другой, но не оба вместе”) или сложение по модулю 2, ее результат равен остатку от деления “обычной” суммы A + B на 2: (А+B) mod 2 Здесь mod обозначает остаток от деления на 2. Обозначение: Ø в естественном языке соответствует сложению двоичных одноразрядных чисел без переноса; Ø в алгебре высказываний обозначение Å; Ø в языках программирования обозначение Xor. Таблица истинности
Свойства операции: A Å B = B Å A
А Å А = 0 А Å Упражнения.
4. Логические выражения Запись сложного высказывания в виде простых высказываний, соединенных логическими связками, называется логической формулой. Напр., «Если мы поедем во Францию, то увидим Эйфелеву башню» - формула: А ® В. Тавталогия – это формула, истинная при любом наборе входящих в нее переменных. Например, x v Ø x (быть или не быть). Противоречие – это формула, ложная при любом наборе входящих в нее переменных. Например, x & Ø x (я и не я). Замечание: При записи выражения учитывается приоритет операций. Высший приоритет имеет операция отрицание, затем конъюнкция, затем дизъюнкция, затем функции. Упражнения на составление формул: 36. Если мистер Джонс счастлив, то мисс Джонс несчастлива, и если мисс Джонс счастлива, то мистер Джонс несчастлив. (А ® 37. Если влажность так высока, то либо после полудня, либо вечером будет дождь. А®(ВvC) 38. Если ни в Варшаву мы не поедем, ни в горы мы не пойдем, то мы ежедневно будем ходить на пляж или если будет дождь, то будем читать книги. 39. Если «Спартак» и «Динамо» проиграет, а «Торпедо» выиграет, то «Локомотив» потеряет первое место, а на третье место выйдет «Зенит». 40. Правильно ли рассуждение: «Если Джонс – коммунист, то Джонс – атеист. Джонс – атеист. Следовательно, Джонс – коммунист. (А ®В) & (В®А)¹ 1 41. Записать выражение. Сформулировать отрицание. «Если летом будет дождливая погода, то ни купаться, ни загорать нам не удастся». 42. Автопилот может работать, если исправен главный бортовой компьютер или два вспомогательных. Выполните формализацию и запишите логические формулы для высказываний “автопилот работоспособен” и “автопилот неработоспособен”.
Любая операция алгебры высказываний может быть выражена через три основные операции: And, Or, Not.
Доказать эти тождества можно построением таблицы истинности. Построить таблицу истинности логического выражения Таблица содержит 1+4 строки (две переменные могут иметь 4 возможных комбинаций значений) и 2+3 столбца (2 переменные и 3 операции). При построении таблицы следует учитывать порядок приоритета выполнения операций: сначала выполняются операции Или, затем логическое следование.
Практическая работа. Построение логических выражений в Excel Построить ТИ выражения Формулы в шапке таблицы выполнить в редакторе формул. Использовать логические функции Excel для получения значений в ячейках таблицы. Замечание. Операция импликация может выполняться функцией ЕСЛИ(условие; выражение1; выражение2), в этом случае условие оставляем пустым, первый аргумент указываем в качестве выражения1, а второй - выражение2. Рассмотрим ряд задач, в которых требуется исследовать логическое выражение.
Задача 1. Каково наибольшее целое число X, при котором истинно высказывание A = (90 < X2) ® (80 > (X + 2)2)
Д/з: 43. Даны два высказывания: A — “В Африке водятся жирафы” и B — “В Мурманске идет снег”. Постройте из них различные сложные высказывания. 44. Почему в таблице истинности для операции “НЕ” две строки, а для других изученных операций — четыре? Сколько строчек в таблице истинности выражения с тремя переменными? с четырьмя? с пятью? Построить таблицы истинности: 45. 46. x ®y Ú x 47. x Ú y ® 48. x®xÚ yÚ z 49. x ®y ®z 50. x «y «z
51. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F. Какие из этих выражений могут соответствовать F? (Ответ: а, б)
а) X б) X Y Z в) г)
52. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F. Какие из этих выражений могут соответствовать F? (Ответ: б, г)
а) б) X в) г) X 53. Определите значение логического выражения (X > 2)→ (X > 3) для X = 1, 2, 3, 4. (Ответ: 1, 1, 0, 1) 54. Определите значение логического выражения ((X < 5)→ (X < 3)) (Ответ: 0, 1, 0, 0) 55. Определите значение логического выражения ((X > 3)+(X < 3))→ (X < 1) для X = 1, 2, 3, 4. (Ответ: 0, 0, 1, 0) 56. Определите значение логического выражения ((X < 4)→ (X < 3)) (Ответ: 0, 0, 0, 1) 57. Найдите все целые значения X, при которых логическое выражение (X > 2)→ (X > 5) ложно. (Ответ: 3, 4, 5) 58. Найдите все целые значения X, при которых логическое выражение ((X > 0)+(X > 4))→ (X > 4) ложно. (Ответ: 1, 2, 3, 4) 59. Каково наибольшее целое положительное число X, при котором истинно высказывание: (X2-1> 100) → (X(X-1)< 100)? (Ответ: 10) 60. Известно, что для чисел A, B и C истинно высказывание
Чему равно A, если C = 10 и B = 22? (Ответ: 21)
5. Логические законы. Закон двойного отрицания:
Любое из этих соотношений можно доказать построением таблицы истинности. Например, докажем закон поглощения A Ú (A & B) = A.
Доказать законы Де Моргана, закон дистрибутивности, законы исключения.
Упражнения: 61. Если я поздно приду на остановку и не смогу сесть в автобус, то опоздаю на занятия и пропущу интересную лекцию. Записать выражение. Сформулировать отрицание. 62. Если завтра будет воскресенье или в институте не будет занятий, то ко мне придут друзья, и мы послушаем музыку. Записать выражение. Сформулировать отрицание. 63. После обеда я отправлюсь на прогулку в парк, и если ко мне зайдет приятель, буду играть с ним в шахматы или мы посмотрим кино. Записать выражение. Сформулировать отрицание.
6. Преобразование логических выражений. Применяя законы логики можно выполнять преобразования логических выражений. Например, докажем законы исключения:
(A & B) Ú ( (A Ú B) & ( Теперь с помощью приведенных законов алгебры логики упростим полученное ранее логическое выражение для объединения областей 3 и 4 на диаграмме Венна с тремя переменными (стр.3):
Здесь мы сначала вынесли общий множитель двух слагаемых за скобки, а затем применили закон исключения третьего. В общем случае можно рекомендовать такую последовательность действий: 1. Заменить все “небазовые” операции (исключающее ИЛИ, импликацию, эквивалентность и др.) на их выражения через базовые операции “НЕ”, “И” и “ИЛИ”. 2. Раскрыть отрицания сложных выражений по законам де Моргана так, чтобы операции отрицания остались только у отдельных переменных. 3. Используя вынесение общих множителей за скобки, раскрытие скобок и другие законы алгебры логики, упростить выражение.
Упражнения. Упростить выражения. Проверить построением таблицы истинности.
67. A Ú ( 68. A & ( 69. (A & B & 70. (A & B & 71. (A Ú B) & ( 72. 73. 74. X®XÚ Y; 75. (XÅ Y) X®Y; 76. (A Ú 77. ((C Ú B) ® B) & (A & B) ® B; 78. ((C Ú B) ® B) & (A Ú B) ® B; 79. (A Å B) & A ®
7. Решение логических уравнений Если приравнять два логических выражения, мы получим уравнение. Его решением будут значения переменных, при которых уравнение превращается в тождество, то есть значения левой и правой частей совпадают. Например, уравнение A× B = 1 имеет единственное решение: A = B = 1, для остальных комбинаций значений переменных левая часть равна нулю. В то же время. уравнение A + B = 1 имеет три решения: (A = 0, B = 1, A = 1, B = 0 и A = B = 1).
8. Решение логических задач.
82. Кто из учеников A, B, C, D играет, а кто не играет в шахматы, если известно следующее: Ø если A или В играет, то С не играет; Ø если В не играет, то играют С и D; Ø С играет. Ответ: играют ученики С и D, а А и В не играют. 83. Кто из трех студентов изучает логику, если известно: Ø Если изучает первый, то изучает и третий, но неверно, что если изучает второй, то изучает третий. Ответ: Второй. 84. На вопрос, какая завтра будет погода, синоптик ответил: Ø если не будет ветра, то будет пасмурно без дождя; Ø если будет дождь, то будет пасмурно и без ветра; Ø если будет пасмурная погода, то будет дождь и не будет ветра. Ответ: будет ясная погода, но с ветром. 85. Определить, кто из четырех студентов сдал экзамены, если известно: Ø Если первый сдал, то и второй сдал; Ø Если второй сдал, то третий сдал или первый не сдал; Ø Если четвертый не сдал, то первый сдал, а третий не сдал; Ø Если четвертый сдал, то и первый сдал. Ответ: все сдали.
|

 «
« = А «В
= А «В
 = А «В
= А «В =1
=1 ) & (
) & ( ® B)
® B)



 =
= 



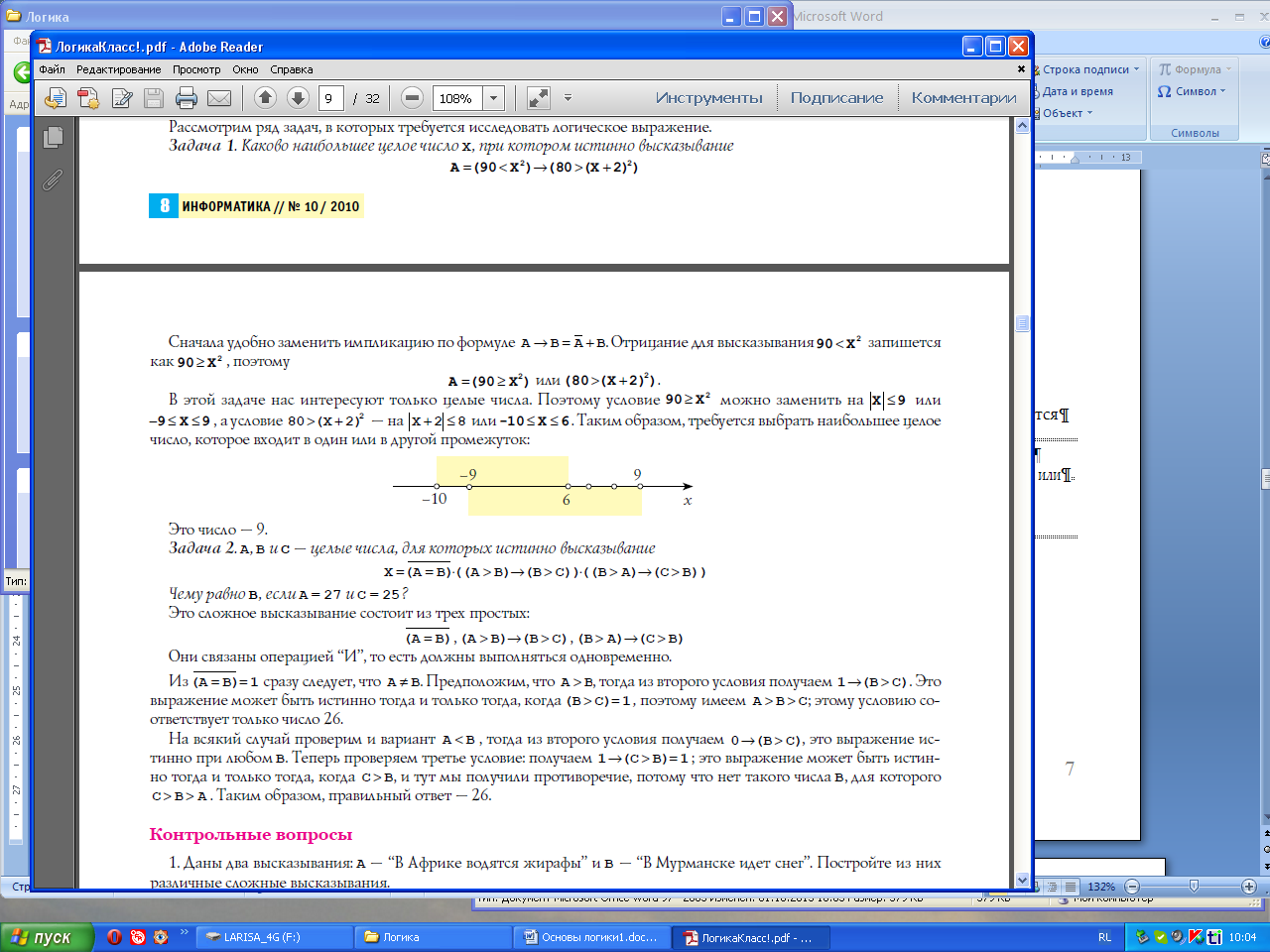
 x Ú
x Ú


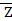
 Y Z
Y Z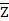
 Y
Y 
 Y
Y 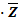
 Z
Z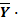 Z
Z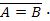 ((B < A)®(2C > A))× ((A < B) ® (A> 2C)).
((B < A)®(2C > A))× ((A < B) ® (A> 2C)). =A
=A = 0
Закон исключенного третьего. Высказывание может быть истинным или ложным,
третьего не дано. А Ú
= 0
Закон исключенного третьего. Высказывание может быть истинным или ложным,
третьего не дано. А Ú 
 Как видим, законы логики симметричны относительно операций “И”, “ИЛИ”:
Как видим, законы логики симметричны относительно операций “И”, “ИЛИ”:


 )= B & 1 = B
)= B & 1 = B +
+ 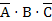 .=(A +
.=(A +  )
)  .=
.= 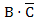
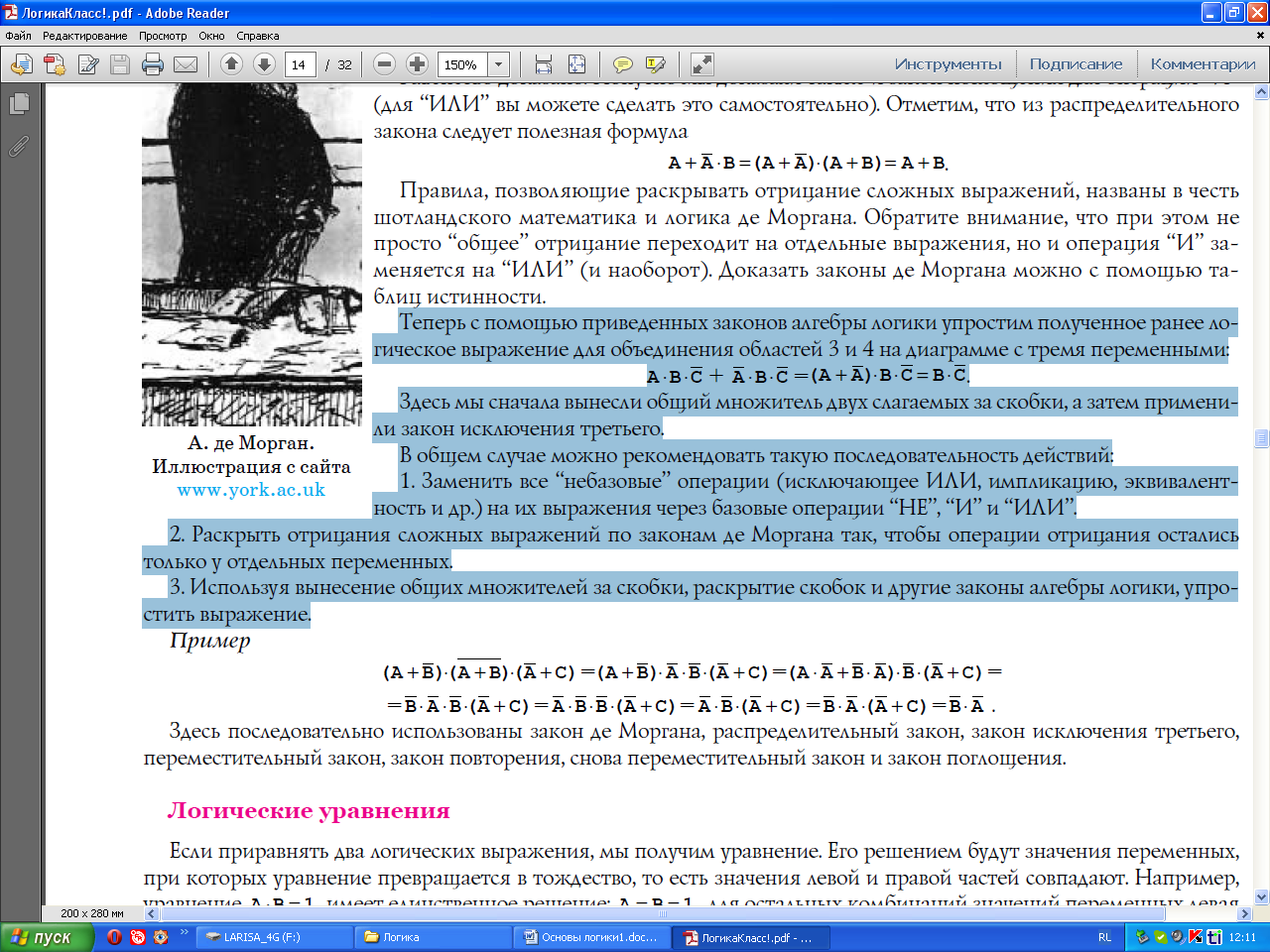

 ) Ú (A &
) Ú (A &  );
); ;
; Ú
Ú  ;
; ;
;