Решение. Методические указания
Методические указания.......... Планы семинарских и практических занятий. Ли- Задания для самостоятельной работы....
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ УО «Белорусский государственный экономический университет»
Л.С. Барковская, Л.В. Станишевская, Ю.Н. Черторицкий
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Практикум
Издание третье, переработанное и дополненное
Минск 2011
СОДЕРЖАНИЕ
ВЕРОЯТНОСТЬ. 1. Пространство элементарных событий.
В основе теории вероятностей лежит понятие случайного эксперимента. Эксперимент считается случайным, если он может закончиться любым из совокупности известных результатов, но до осуществления эксперимента нельзя предсказать, каким именно. Примеры случайного эксперимента: бросание монеты, игральной кости, проведение лотереи, азартные игры, стрельба по цели, поступление звонков на телефонную станцию и т.п. Различные результаты эксперимента называют исходами. Определение 1. Множество всех взаимоисключающих исходов эксперимента называется пространством элементарных событий. Взаимоисключающие исходы — это те, которые не могут наступить одновременно. Пространство элементарных событий будем обозначать буквой Ω, а его исходы — буквой ω. Определение 2. Произвольное подмножество пространства элементарных событий называется событием. Событие может состоять из одного или нескольких элементарных событий, а также из счетного или несчетного числа элементарных событий. Событие Ω, состоящее из всех исходов эксперимента, называется достоверным событием. Оно обязательно происходит, так как эксперимент всегда заканчивается каким-нибудь исходом. Пустое множество исходов эксперимента называется невозможным событием и обозначается символом ø. Определение 3. Суммой двух событий А и В (обозначается Определение 4. Произведением двух событий А и В (обозначается АВ) называется событие, состоящее из тех исходов, которые входят как в А, так и в В. Иными словами, АВ означает событие, при котором события А и В наступают одновременно (рис. 1.1б). Определение 5. Разностью двух событий А и В (обозначается Смысл события Определение 6. Противоположным(дополнительным) для события А (обозначается Если события изобразить на плоскости, то результат определенных операций над событиями выглядит следующим образом:
Рис. 1.1 Определение 7. События А и В называются несовместимыми, если нет исходов, входящих как в А, так и в В, т.е. АВ = ø. Определение 8. Говорят, что событие А содержится в событии В (обозначается
Свойства операций над событиями
Пример 1.1. Два шахматиста играют подряд две партии. Под исходом опыта будем понимать выигрыш одного из них в i -й партии или ничью. Построить пространство Решение. Обозначим события 1. Обе партии выиграл первый игрок 2. Обе партии выиграл второй игрок 3. Обе партии закончились вничью 4. В первой партии выиграл первый игрок, во второй — второй 5. В первой выиграл первый игрок, во второй — ничья 6. В первой партии победа второго игрока, во второй — первого 7. В первой — победа второго игрока, во второй — ничья 8. В первой — ничья, во второй — победа первого игрока 9. В первой — ничья, во второй — победа второго игрока Ответ:
Пример 1.2. Пусть А, В, С — три произвольных события. Найти выражения для событий, состоящих в том, что из А, В, С: 1. Произошло только А. 2. Произошло А и В, но С не произошло. 3. Все три события произошли. 4. Произошло, по крайней мере, одно из событий. 5. Произошли, по крайней мере, два события. 6. Произошло одно и только одно событие. 7. Произошли два и только два события. 8. Ни одно событие не произошло. 9. Произошло не более двух событий. Решение. 1. Обозначим 2. 3. 4. Событие произошло, по крайней мере, одно из событий можно представить как сумму этих событий: А + В + С. 5. Произошли, по крайней мере, два события — это сумма АВ + АС + ВС. 6. Произошло одно и только одно событие — это сумма событий 7. Произошли два и только два события — можно записать в виде 8. 9. Пример 1.3. События А, В и С означают, что взято хотя бы по одной книге из трех различных собраний сочинений, каждое из которых содержит по крайней мере три тома. События
|
) называется событие, состоящее из всех исходов, входящих либо в А, либо в В. Другими словами, под 
) называется событие, состоящее из исходов, входящих в А, но не входящих в В.
) называется событие, состоящее из всех исходов, которые не входят в А. Наступление события 
), если все исходы события А входят в событие В.
;
;
;
;
;
ø;
;
;
;
;
;
.
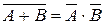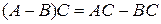элементарных исходов.
— в i -й партии выиграл первый игрок, 
— второй, С — ничья. Тогда возможные исходы игры:
.
.
.
.
.
.
.
.
.
= 
, 
.
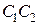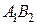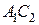и 
, что события В и С не произошли, тогда событие: произошло только А можно записать в виде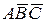 
.
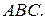
, или АВ + АС + ВС – АВС.
, т.е. три события одновременно не произошли.
и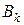 
означают соответственно, что из первого собрания сочинений взяты s, а из второго k томов. Что означают события: а) А +
; г) 
; д) 
?
