Закон больших чисел
Следующие утверждения и теоремы составляют содержание группы законов, объединенных общим названием закон больших чисел. Лемма 1 (неравенство Маркова). Пусть Х — неотрицательная случайная величина, т.е.
где М (Х) — математическое ожидание Х. Следствие 1. Так как события
Пример 9.1. Оценить вероятность того, что в течение ближайшего дня потребность в воде в населенном пункте превысит 150 000 л, если среднесуточная потребность в ней составляет 50 000 л. Решение. Используя неравенство Маркова в виде Ответ:
Пример 9.2. Среднее число солнечных дней в году для данной местности равно 90. Оценить вероятность того, что в течение года в этой местности будет не более 240 солнечных дней. Решение. Согласно неравенству Ответ:
Лемма 2 (неравенство Чебышева). Для любой случайной величины Х, имеющей конечную дисперсию и любого
Следствие 2. Для любой случайной величины Х с конечной дисперсией и любого
Пример 9.3. Длина изготавливаемых деталей является случайной величиной, среднее значение которой 50 мм. Среднеквадратичное отклонение этой величины равно 0, 2 мм. Оценить вероятность того, что отклонение длины изготовленной детали от ее среднего значения по абсолютной величине не превзойдет 0, 4 мм. Решение. Для оценки вероятности используем неравенство Чебышева
Ответ:
Пример 9.4. Среднесуточное потребление электроэнергии в населенном пункте равно 20 000 кВт/ч, а среднеквадратичное отклонение — 200 кВт/ч. Какого потребления электроэнергии в этом населенном пункте можно ожидать в ближайшие сутки с вероятностью, не меньшей 0, 96? Решение. Воспользуемся неравенством Чебышева
Следовательно, в этом населенном пункте можно ожидать с вероятностью не меньшей 0, 96 потребление электроэнергии Ответ: от 19 000 до 21 000.
Теорема Чебышева. Если
При доказательстве предельного равенства используется неравенство
которое вытекает из неравенства Чебышева.
Пример 9.5. За значение некоторой величины принимают среднеарифметическое достаточно большого числа ее измерений. Предполагая, что среднеквадратичное отклонение возможных результатов каждого измерения не превосходит 5 мм, оценить вероятность того, что при 1000 измерений неизвестной величины отклонение принятого значения от истинного по абсолютной величине не превзойдет 0, 5 мм. Решение. Воспользуемся неравенством
По условию
Ответ:
Частными случаями теоремы Чебышева являются теоремы Бернулли и Пуассона.
Теорема Бернулли. При неограниченном увеличении числа независимых опытов частость появления
где При доказательстве теоремы Бернулли получаем такую оценку
Теорема Пуассона. Если производится
где
имеющее практическое применение.
Пример 9.6. При контрольной проверке изготавливаемых приборов было установлено, что в среднем 15 шт. из 100 оказывается с теми или иными дефектами. Оценить вероятность того, что доля приборов с дефектами среди 400 изготовленных будет по абсолютной величине отличаться от математического ожидания этой доли не более чем на 0, 05. Решение. Воспользуемся неравенством
По условию Итак, Ответ:
Пример 9.7. Вероятность того, что изделие является качественным, равна 0, 9. Сколько следует проверить изделий, чтобы с вероятностью не меньшей 0, 95 можно было утверждать, что абсолютная величина отклонения доли качественных изделий от 0, 9 не превысит 0, 01? Решение. Воспользуемся неравенством
По условию
Ответ:
|

 . Тогда для любого
. Тогда для любого 
 ,
, и
и  противоположные, то неравенство Маркова можно записать в виде
противоположные, то неравенство Маркова можно записать в виде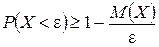 .
.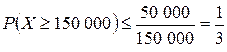 .
. .
. , имеем
, имеем 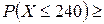
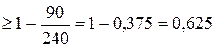 .
. .
. .
. .
. .
. .
.
 . Подставим в правую часть неравенства вместо
. Подставим в правую часть неравенства вместо  величину
величину  , сделаем ее большей или равной 0, 96:
, сделаем ее большей или равной 0, 96: .
.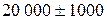 , т.е.
, т.е.  .
. последовательность независимых случайных величин с математическими ожиданиями
последовательность независимых случайных величин с математическими ожиданиями  и дисперсиями
и дисперсиями  , ограниченными одной и той же постоянной
, ограниченными одной и той же постоянной  , то какова бы ни была постоянная
, то какова бы ни была постоянная 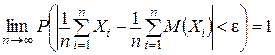 .
. ,
, ,
,  ,
,  Итак, искомая вероятность
Итак, искомая вероятность

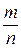 некоторого события А сходится по вероятности к его вероятности р = Р (А):
некоторого события А сходится по вероятности к его вероятности р = Р (А): ,
, — сколь угодно малое положительное число.
— сколь угодно малое положительное число.
 , которая применяется на практике.
, которая применяется на практике. независимых опытов и вероятность появления события А в
независимых опытов и вероятность появления события А в  -м опыте равна
-м опыте равна 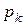 , то при увеличинении
, то при увеличинении 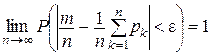 ,
, ,
, .
. ,
,  . В качестве р возьмем величину, полученную при проверке для доли брака
. В качестве р возьмем величину, полученную при проверке для доли брака  .
.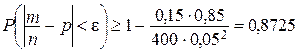 .
.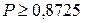 .
. ,
,  ,
,  . Подставим в правую часть вышеприведенного неравенства эти значения
. Подставим в правую часть вышеприведенного неравенства эти значения .
.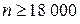 .
.


