Задачи для самостоятельного решения. 8.31. Цена деления шкалы измерительного прибора равна 0,1
8.31. Цена деления шкалы измерительного прибора равна 0, 1. Показания прибора округляют до ближайшего целого деления. Полагая, что при отсчете ошибка округления распределена по равномерному закону, найти: 1) математическое ожидание, дисперсию и среднее квадратическое отклонение этой случайной величины; 2) вероятность того, что ошибка округления: а) меньше 0, 01; б) больше 0, 03. Ответ: 1) 2а) 2б)
8.32. Автобусы некоторого маршрута идут строго по расписанию. Интервал движения 4 мин. Найти вероятность того, что пассажир, подошедший к остановке, будет ожидать очередной автобус менее 2 мин. Ответ:
8.33. Минутная стрелка часов перемещается скачком в конце каждой минуты. Найти вероятность того, что в данное мгновение часы покажут время, которое отличается от истинного не более чем на 10 с. Ответ: 8.34. Случайные величины Х и Ответ:
8.35. Диаметр круга х измерен приближенно, причем Ответ: 8.36. Ребро куба х измерено приближенно, причем Ответ:
8.37. Пусть случайные величины Ответ:
8.38. Случайная величина Х равномерно распределена на отрезке
Ответ: 1) 2) 3)
8.39. В здании областной администрации случайное время ожидания лифта равномерно распределено в диапазоне от 0 до 5 мин. Найти: а) функцию распределения
Ответ: а)
8.40. Мастер, осуществляющий ремонт на дому, может появиться в любое время с 10 до 18 часов. Клиент, прождав до 14 часов, отлучился на 1 час. Какова вероятность, что мастер (приход его обязателен) не застанет его дома? Ответ: 0, 125.
8.41. Владелец антикварного аукциона полагает, что предложение цены за определенную картину будет равномерно распределенной случайной величиной в интервале от 500 тыс. до 2 млн. рублей. Найти: а) плотность вероятности; б) вероятность того, что картина будет продана за цену, меньшую чем 675 тыс.; в) вероятность того, что цена картины будет выше 2 млн. рублей.
Ответ:
8.42. Очень наблюдательный, занимающийся кражей предметов искусства вор, который, вероятно, знает хорошо статистику, заметил, что частота, с которой охранники обходят музей, равномерно распрелена между 15 и 60 минутами. Пусть случайная величчина Х – время (в минутах) до появления охраны. Найти: а) вероятность того, что охранник появится в течение 35 минут после появления вора; б) вероятность того, что охрана не появится в течение 30 минут; в) вероятность того, что охрана появится между 35 и 45 минутами после прихода вора; г) функцию распределения Ответ: а) 0, 4444; б) 0, 6667; в) 0, 2222; г)
8.43. На перекрестке дорог движение регулируется автоматическим светофором, включающим зеленый свет через каждые 2 минуты. Время простоя у этого светофора автомобиля, остановившегося на красный свет, есть случайная величина, распределенная равномерно на интервале (0; 2) минут. Найти среднее время простоя и среднее квадратическое отклонение. Ответ:
|





 .
. независимы и распределены равномерно: Х — в интервале
независимы и распределены равномерно: Х — в интервале  ,
,  . Найти математическое ожидание и дисперсию произведения
. Найти математическое ожидание и дисперсию произведения 
 ;
; 
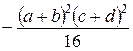 .
. . Рассматривая диаметр как случайную величину Х, распределенную равномерно в интервале
. Рассматривая диаметр как случайную величину Х, распределенную равномерно в интервале  , найти математическое ожидание и дисперсию площади круга.
, найти математическое ожидание и дисперсию площади круга. .
. . Рассматривая длину ребра куба как случайную величину Х, распределенную равномерно в интервале
. Рассматривая длину ребра куба как случайную величину Х, распределенную равномерно в интервале  , найти математическое ожидание и дисперсию объема куба.
, найти математическое ожидание и дисперсию объема куба. .
. и
и  независимы и равномерно распределены на отрезке
независимы и равномерно распределены на отрезке  . Найти вероятность того, что
. Найти вероятность того, что  .
. .
. . 1) Записать плотность распределения р (х) этой случайной величины. 2) Найти функцию распределения
. 1) Записать плотность распределения р (х) этой случайной величины. 2) Найти функцию распределения  . 3) Найти математическое ожидание, дисперсию и среднее квадратическое отклонение этой случайной величины.
. 3) Найти математическое ожидание, дисперсию и среднее квадратическое отклонение этой случайной величины.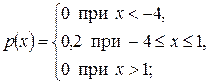

 .
. для этого равномерного распределения; б) вероятность ожидания лифта более чем 3, 5 мин; в) вероятность того, что лифт прибудет в течение первых 45 секунд; г) вероятность того, что ожидание лифта будет заключено в диапазоне от 1 до 3 мин. (между 1 и 3 минутами).
для этого равномерного распределения; б) вероятность ожидания лифта более чем 3, 5 мин; в) вероятность того, что лифт прибудет в течение первых 45 секунд; г) вероятность того, что ожидание лифта будет заключено в диапазоне от 1 до 3 мин. (между 1 и 3 минутами). б) 0, 3; в) 0, 15; г) 0, 4.
б) 0, 3; в) 0, 15; г) 0, 4. б) 0, 1167; в) 0.
б) 0, 1167; в) 0.
 ;
;  .
.


