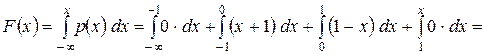Решение. Все значения этой функции принадлежат отрезку , т.е
Рис. 8.4
Все значения этой функции принадлежат отрезку
Выполняются и равенства:
Следовательно, функция
Пример 8.3. Является ли функцией распределения некоторой случайной величины функция
Решение. Данная функция не является функцией распределения случайной величины, так как на промежутке
Рис. 8.5
Пример 8.4. Случайная величина Х задана функцией распределения
Найти коэффициент а и плотность вероятности случайной величины Х. Определить вероятность неравенства Решение. Плотность распределения равна первой производной от функции распределения
Коэффициент а определяем с помощью равенства
отсюда
Тот же результат можно было получить, используя непрерывность функции
Следовательно, Поэтому плотность вероятности имеет вид
Вероятность
Пример 8.5. Случайная величина Х имеет плотность вероятности (закон Коши)
Найти коэффициент а и вероятность того, что случайная величина Х примет какое-нибудь значение из интервала Решение. Найдем коэффициент а из равенства
но Следовательно, Итак, Вероятность того, что случайная величина Х примет какое-нибудь значение из интервала
Найдем функцию распределения данной случайной величины
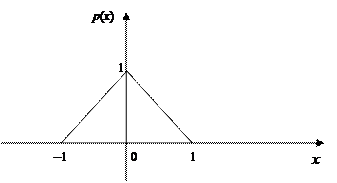
Пример 8.6. График плотности вероятности случайной величины Х изображен на рис. 8.6 (закон Симпсона). Написать выражение плотности вероятности ифункцию распределения этой случайной величины. Рис. 8.6 Решение. Пользуясь графиком, записываем аналитическое выражение плотности распределения вероятностей данной случайной величины
Найдем функцию распределения. Если Если Если
Если
Следовательно, функция распределения имеет вид
|

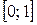 , т.е.
, т.е.  . Функция F (х) является неубывающей: в промежутке
. Функция F (х) является неубывающей: в промежутке  она постоянна, равна нулю, в промежутке
она постоянна, равна нулю, в промежутке 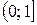 возрастает, в промежутке
возрастает, в промежутке  также постоянна, равна единице (см. рис. 8.4). Функция непрерывна в каждой точке х 0 области ее определения — промежутка
также постоянна, равна единице (см. рис. 8.4). Функция непрерывна в каждой точке х 0 области ее определения — промежутка 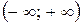 , поэтому непрерывна слева, т.е. выполняется равенство
, поэтому непрерывна слева, т.е. выполняется равенство
 ,
,  .
. ,
,  .
. удовлетворяет всем свойствам, характерным для функции распределения. Значит данная функция
удовлетворяет всем свойствам, характерным для функции распределения. Значит данная функция 
 она убывает и не является непрерывной. График функции изображен на рис. 8.5.
она убывает и не является непрерывной. График функции изображен на рис. 8.5.

 .
.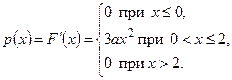
 ,
, .
.
 ,
,  .
. .
.
 попадания случайной величины Х в заданный промежуток вычисляется по формуле
попадания случайной величины Х в заданный промежуток вычисляется по формуле .
. .
. . Найти функцию распределения этой случайной величины.
. Найти функцию распределения этой случайной величины. ,
,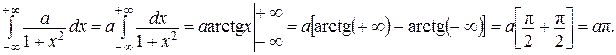
 .
. .
.


 , то
, то  .
. , то
, то  .
. , то
, то 

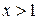 , то
, то