Задачи для самостоятельного решения. Показать, что данная функция является функцией распределения некоторой случайной величины Х
8.1. Дана функция
Показать, что данная функция является функцией распределения некоторой случайной величины Х. Найти вероятность того, что эта случайная величина принимает значения из интервала Ответ:
8.2. Дана функция
Является ли она функцией распределения некоторой случайной величины? Ответ: нет.
8.3. Является ли функцией распределения некоторой случайной величины функция
Ответ: нет.
8.4. Является ли функцией распределения некоторой случайной величины каждая из следующих функций: а)
б) Ответ: а) да; б) нет.
8.5. Дана функция распределения случайной величины Х:
Найти плотность вероятности, а также вероятности Ответ:
8.6. Случайная величина Х, сосредоточенная на интервале Ответ:
8.7. Случайная величина Х, сосредоточенная на интервале Ответ:
8.8. Случайная величина Х, сосредоточенная на интервале Ответ:
8.9. Функция распределения случайной величины Х имеет вид
Определить постоянные а и b. Найти плотность вероятности случайной величины Х и построить ее график. Ответ:
8.10. Плотность распределения вероятностей случайной величины Х определяется функцией
Найти значение коэффициента а. Найти функцию распределения F (х) величины Х. Ответ: 8.11. Функция р (х) задана в виде
Найти значение постоянной а, при которой функция будет плотностью вероятности некоторой случайной величины Х; функцию распределения F (х); вычислить вероятность того, что случайная величина Х примет значение на отрезке Ответ:
8.12. Задана плотность распределения непрерывной случайной величины Х:
Найти функцию распределения F (х). Ответ: 8.13. Плотность распределения непрерывной случайной величины Х в интервале Ответ: 8.14. Функция распределения случайной величины Х имеет вид Ответ:
|


 .
.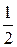 .
.
 ?
?



 .
.
 .
.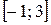 , задана функцией распределения
, задана функцией распределения  . Найти вероятность попадания случайной величины Х в интервал
. Найти вероятность попадания случайной величины Х в интервал  . Построить график функции F (х).
. Построить график функции F (х). .
. , задана функцией распределения
, задана функцией распределения  . Найти вероятность того, что случайная величина Х примет значения: а) меньше 4; б) меньше 6; в) не меньше 3; г) не меньше 6.
. Найти вероятность того, что случайная величина Х примет значения: а) меньше 4; б) меньше 6; в) не меньше 3; г) не меньше 6. .
. , задана квадратичной функцией
, задана квадратичной функцией  , имеющей максимум при х = 4. Найти параметры а, b, с и вычислить вероятность попадания случайной величины Х в интервал
, имеющей максимум при х = 4. Найти параметры а, b, с и вычислить вероятность попадания случайной величины Х в интервал  .
. .
.

 .
. .
.
 .
.
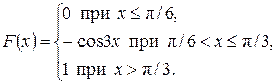
 равна
равна  ; вне этого интервала р (х) = 0. Найти вероятность того, что в трех независимых испытаниях Х примет два раза значение, заключенное в интервале
; вне этого интервала р (х) = 0. Найти вероятность того, что в трех независимых испытаниях Х примет два раза значение, заключенное в интервале  .
. .
. Определить постоянные а, b и найти плотность распределения вероятностей р(х).
Определить постоянные а, b и найти плотность распределения вероятностей р(х).



