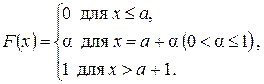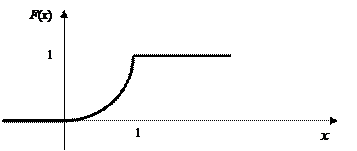Для непрерывной случайной величины
Все свойства функций распределения дискретных случайных величин выполняются и для функций распределения непрерывных случайных величин. Задание непрерывной случайной величины с помощью функции распределения не является единственным. Плотностью вероятности (плотностью распределения или плотностью) р (х) непрерывной случайной величины Х называется производная ее функции распределения
Плотность вероятности р (х), как и функция распределения F (х), является одной из форм закона распределения, но в отличие от функции распределения она существует только для непрерывных случайных величин. Плотность вероятности иногда называют дифференциальной функцией, или дифференциальным законом распределения. График плотности вероятности называется кривой распределения. Свойства плотности вероятности непрерывной случайной величины:
1. 2.
Рис. 8.1
3.
Рис. 8.2 4. Геометрически свойства плотности вероятности означают, что ее график — кривая распределения — лежит не ниже оси абсцисс, и полная площадь фигуры, ограниченной кривой распределения и осью абсцисс, равна единице.
Пример 8.1. Минутная стрелка электрических часов передвигается скачками поминутно. Вы бросили взгляд на часы. Они показывают а минут. Тогда для вас истинное время в данный момент будет случайной величиной. Найти ее функцию распределения. Решение. Очевидно, что функция распределения истинного времени равна 0 для всех
Она непрерывна всюду, а производная ее непрерывна во всех точках, за исключением двух: х = а и х = а + 1. График этой функции имеет вид (рис. 8.3):
Рис. 8.3
Пример 8.2. Является ли функцией распределения некоторой случайной величины функция

|

 .
.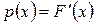 .
.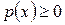 .
.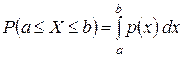 (рис. 8.1).
(рис. 8.1).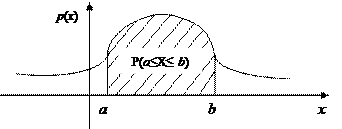
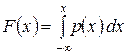 (рис. 8.2).
(рис. 8.2).
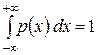 .
.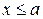 и единице для
и единице для 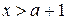 . Время течет равномерно. Поэтому вероятность того, что истинное время меньше а + 0, 5 мин, равна 0, 5, так как одинаково вероятно, прошло ли после а менее или более полминуты. Вероятность того, что истинное время меньше а + 0, 25 мин, равна 0, 25 (вероятность этого времени втрое меньше вероятности того, что истинное время больше а + 0, 25 мин, а сумма их равна единице, как сумма вероятностей противоположных событий). Аналогично рассуждая, найдем, что вероятность того, что истинное время меньше а + 0, 6 мин, равна 0, 6. В общем случае вероятность того, что истинное время меньше а + + α мин
. Время течет равномерно. Поэтому вероятность того, что истинное время меньше а + 0, 5 мин, равна 0, 5, так как одинаково вероятно, прошло ли после а менее или более полминуты. Вероятность того, что истинное время меньше а + 0, 25 мин, равна 0, 25 (вероятность этого времени втрое меньше вероятности того, что истинное время больше а + 0, 25 мин, а сумма их равна единице, как сумма вероятностей противоположных событий). Аналогично рассуждая, найдем, что вероятность того, что истинное время меньше а + 0, 6 мин, равна 0, 6. В общем случае вероятность того, что истинное время меньше а + + α мин 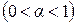 , равна α. Следовательно, функция распределения истинного времени имеет следующее выражение:
, равна α. Следовательно, функция распределения истинного времени имеет следующее выражение: