Равномерный закон распределения
Непрерывная случайная величина Х имеет равномерный закон распределения на отрезке
Функция распределения случайной величины Х, распределенной по равномерному закону, есть
Математическое ожидание Пример 8.14. Поезда метрополитена идут регулярно с интервалом 3 мин. Пассажир выходит на платформу в случайный момент времени. Какова вероятность того, что ждать пассажиру придется не больше минуты. Найти математическое ожидание и среднее квадратическое отклонение случайной величины Х — времени ожидания поезда. Решение. Случайная величина Х — время ожидания поезда на временном (в минутах) отрезке
Рис. 8.11 Пример 8.15. Найти математическое ожидание и дисперсию произведения двух независимых случайных величин ξ и η с равномерными законами распределения: ξ в интервале Решение. Так как математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий, то
Аналогично рассчитаем
Следовательно,
Пример 8.16. Вычислить математическое ожидание и дисперсию определителя
элементы которого Решение. Вычислим математическое ожидание
Для нахождения дисперсии Действительно,
Следовательно,
Замечание. Для определителя n -го порядка
Пример 8.17. Автоматический светофор работает в двух режимах: 1 мин. горит зеленый свет и 0, 5 мин — красный и т.д. Водитель подъезжает к перекрестку в случайный момент времени. 1. Найти вероятность того, что он проедет перекресток без остановки. 2. Составить закон распределения и вычислить числовые характеристики времени ожидания у перекрестка. Решение. 1. Момент проезда автомобиля t через перекресток распределен равномерно в интервале, равном периоду смены цветов светофора. Этот период равен 1 + 0, 5 = 1, 5 мин. Для того чтобы машина проехала через перекресток не останавливаясь, достаточно того, чтобы момент проезда пришелся на интервал времени
2. Время ожидания
Рис. 8.12
То есть Среднее время ожидания у перекрестка
Дисперсия времени ожидания
|

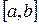 , если ее плотность вероятности р (х) постоянна на этом отрезке и равна нулю вне его, т.е.
, если ее плотность вероятности р (х) постоянна на этом отрезке и равна нулю вне его, т.е.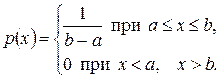
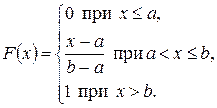
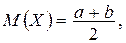 дисперсия
дисперсия  а среднее квадратическое отклонение
а среднее квадратическое отклонение 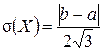 .
.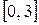 имеет равномерный закон распределения
имеет равномерный закон распределения 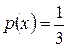 . Поэтому вероятность того, что пассажиру придется ждать не более минуты, равна
. Поэтому вероятность того, что пассажиру придется ждать не более минуты, равна  от равной единице площади прямоугольника (рис. 8.11), т.е.
от равной единице площади прямоугольника (рис. 8.11), т.е.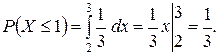
 мин,
мин, 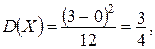
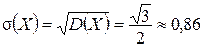 мин.
мин.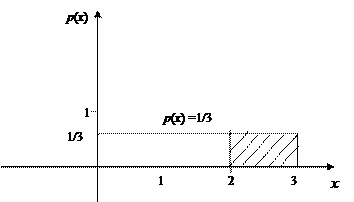
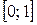 , η — в интервале
, η — в интервале 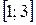 .
.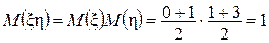 . Для нахождения дисперсии воспользуемся формулой
. Для нахождения дисперсии воспользуемся формулой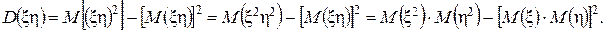
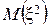 найдем по формуле
найдем по формуле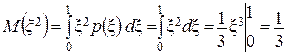 .
. .
. .
. ,
,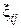 — независимые случайные величины с
— независимые случайные величины с 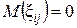 и
и 

 докажем, что если ξ и η — независимые случайные величины, то
докажем, что если ξ и η — независимые случайные величины, то 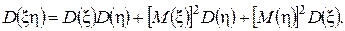
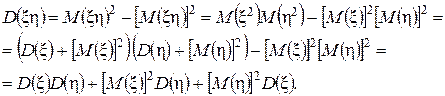
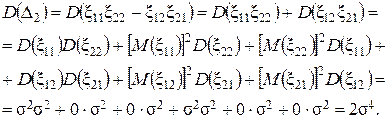
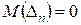 ;
; 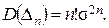
 . Тогда
. Тогда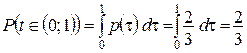 .
.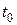 является смешанной случайной величиной: с вероятностью
является смешанной случайной величиной: с вероятностью 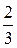 она равна нулю, а с вероятностью
она равна нулю, а с вероятностью 
 при
при 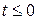 ;
; 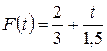 при
при 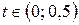 ;
; 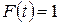 при
при 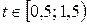 .
. мин.
мин.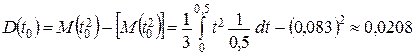 мин2;
мин2; мин.
мин.


