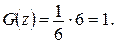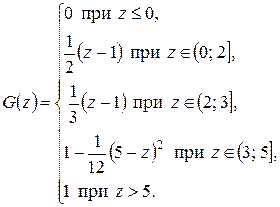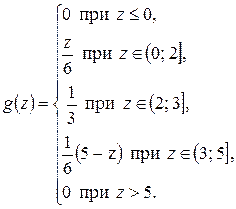Если каждой паре возможных случайных величин Х и  соответствует одно возможное значение случайной величины
соответствует одно возможное значение случайной величины 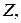 то
то 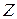 называют функцией двух случайных аргументов Х и
называют функцией двух случайных аргументов Х и  и пишут
и пишут
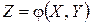 .
.
Если Х и  дискретные независимые случайные величины, то для нахождения распределения функции
дискретные независимые случайные величины, то для нахождения распределения функции 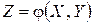 , надо найти все возможные значения
, надо найти все возможные значения  , для чего достаточно для каждого возможного значения Х, равного
, для чего достаточно для каждого возможного значения Х, равного  , и каждого возможного значения
, и каждого возможного значения  равного
равного 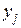 , вычислить значение
, вычислить значение 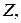 равное
равное 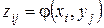 . Вероятности найденных возможных значений
. Вероятности найденных возможных значений 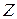 равны произведениям вероятностей
равны произведениям вероятностей 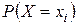 и
и 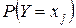 .
.
Пример 10.6. Дискретные независимые случайные величины Х и  заданы распределениями:
заданы распределениями:
| Х
| –2
| –1
|
|
|
| Р
| 0, 3
| 0, 1
| 0, 5
| 0, 1
|
Найти распределения случайных величин: а) 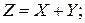 б)
б) 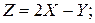 в)
в)  г)
г) 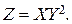
Решение. Для того чтобы составить указанные распределения величины 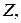 надо найти все возможные значения
надо найти все возможные значения 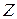 и их вероятности. Все вычисления поместим в таблицу
и их вероятности. Все вычисления поместим в таблицу
| Х
| 
| 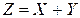
| 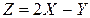
| 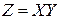
|  2 2
| 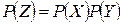
|
| –2
|
| –1
| –5
| –2
| –2
| 0, 3 · 0, 4 = 0, 12
|
| –2
|
|
| –6
| –4
| –8
| 0, 3 · 0, 1 = 0, 03
|
| –2
|
|
| –7
| –6
| –18
| 0, 3 · 0, 5 = 0, 15
|
| –1
|
|
| –3
| –1
| –1
| 0, 1 · 0, 4 = 0, 04
|
| –1
|
|
| –4
| –2
| –4
| 0, 1 · 0, 1 = 0, 01
|
| –1
|
|
| –5
| –3
| –9
| 0, 1 · 0, 5 = 0, 05
|
|
|
|
|
|
|
| 0, 5 · 0, 4 = 0, 20
|
|
|
|
|
|
|
| 0, 5 · 0, 1 = 0, 05
|
|
|
|
|
|
|
| 0, 5 · 0, 5 = 0, 25
|
|
|
|
|
|
|
| 0, 1 · 0, 4 = 0, 04
|
|
|
|
|
|
|
| 0, 1 · 0, 1 = 0, 01
|
|
|
|
|
|
|
| 0, 1 · 0, 5 = 0, 05
|
|
|
|
|
|
|
| 1, 00
|
Объединив одинаковые значения 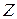 и расположив их в порядке возрастания, получим следующие распределения:
и расположив их в порядке возрастания, получим следующие распределения:
а)
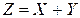
| –1
|
|
|
|
|
|
|
|
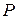
| 0, 12
| 0, 07
| 0, 16
| 0, 05
| 0, 20
| 0, 09
| 0, 26
| 0, 05
|
б)
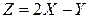
| –7
| –6
| –5
| –4
| –3
|
|
|
|
|
|
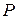
| 0, 15
| 0, 03
| 0, 17
| 0, 01
| 0, 04
| 0, 25
| 0, 05
| 0, 25
| 0, 01
| 0, 04
|
в)
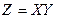
| –6
| –4
| –3
| –2
| –1
|
|
|
|
|
|
|
| 0, 15
| 0, 03
| 0, 05
| 0, 13
| 0, 04
| 0, 20
| 0, 04
| 0, 05
| 0, 01
| 0, 25
| 0, 05
|
г)

| –18
| –9
| –8
| –4
| –2
| –1
|
|
|
|
|
|
|
| 0, 15
| 0, 05
| 0, 03
| 0, 01
| 0, 12
| 0, 04
| 0, 2
| 0, 04
| 0, 05
| 0, 01
| 0, 25
| 0, 05
|
Если Х и  непрерывные независимые случайные величины, то плотность распределения
непрерывные независимые случайные величины, то плотность распределения 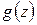 суммы
суммы 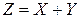 (при условии, что плотность распределения хотя бы одного из аргументов задана в интервале
(при условии, что плотность распределения хотя бы одного из аргументов задана в интервале  одной формулой) может быть найдена по формуле
одной формулой) может быть найдена по формуле
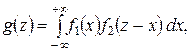
либо по равносильной формуле
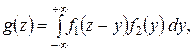
где 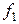 и
и 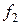 — плотности распределения аргументов.
— плотности распределения аргументов.
Если возможные значения аргументов неотрицательны, то плотность распределения 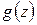 величины
величины 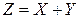 находят по формуле
находят по формуле
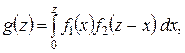
либо по равносильной формуле
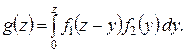
В том случае, когда обе плотности 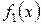 и
и 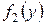 заданы на конечных интервалах, для отыскания плотности
заданы на конечных интервалах, для отыскания плотности 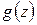 величины
величины 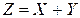 целесообразно сначала найти функцию распределения
целесообразно сначала найти функцию распределения 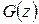 , а затем продифференцировать ее по
, а затем продифференцировать ее по 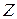
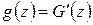 .
.
Если Х и  — независимые случайные величины, заданные соответствующими плотностями распределения
— независимые случайные величины, заданные соответствующими плотностями распределения 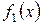 и
и 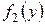 , то вероятность попадания случайной точки
, то вероятность попадания случайной точки 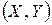 в область
в область 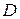 равна двойному интегралу по этой области от произведения плотностей распределения
равна двойному интегралу по этой области от произведения плотностей распределения
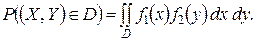
Пример 10.7. Независимые нормально распределенные случайные величины Х и  заданы плотностями распределений
заданы плотностями распределений 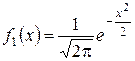 ,
, 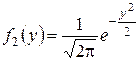 . Найти композицию этих законов, т.е. плотность распределения случайной величины
. Найти композицию этих законов, т.е. плотность распределения случайной величины 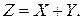
Решение. Используем формулу 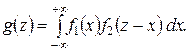 Тогда
Тогда
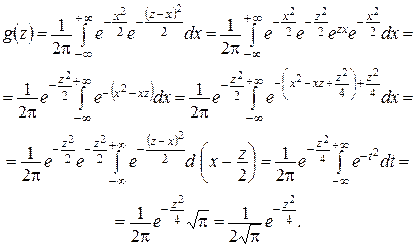
Ответ: 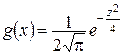 .
.
Пример 10.8. Заданы плотности распределения независимых равномерно распределенных случайных величин Х и 
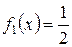 в интервале (0; 2), вне этого интервала
в интервале (0; 2), вне этого интервала  ,
, 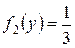 в интервале (0; 3), вне этого интервала
в интервале (0; 3), вне этого интервала  . Найти функцию распределения и плотность распределения случайной величины
. Найти функцию распределения и плотность распределения случайной величины 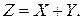 Построить график распределения
Построить график распределения  .
.
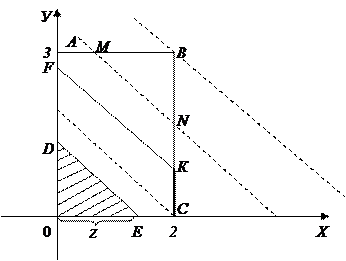 Решение. По условию, возможные значения Х определяются неравенством
Решение. По условию, возможные значения Х определяются неравенством 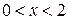 ,
,  — неравенством
— неравенством 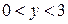 . Отсюда следует, что возможные случайные точки
. Отсюда следует, что возможные случайные точки 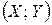 расположены в прямоугольнике ОАВС (рис. 10.1).
расположены в прямоугольнике ОАВС (рис. 10.1).
Рис. 10.1
Неравенству 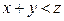 удовлетворяют те точки
удовлетворяют те точки 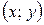 плоскости
плоскости 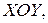 которые лежат ниже прямой
которые лежат ниже прямой 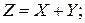 если же брать только возможные значения х и у, то неравенство
если же брать только возможные значения х и у, то неравенство 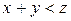 выполняется только для точек, лежащих в прямоугольнике ОАВС ниже прямой
выполняется только для точек, лежащих в прямоугольнике ОАВС ниже прямой 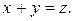 С другой стороны, так как величины Х и
С другой стороны, так как величины Х и  независимы, то
независимы, то

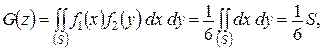
где 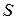 — величина той части площади прямоугольника ОАВС, которая лежит ниже прямой
— величина той части площади прямоугольника ОАВС, которая лежит ниже прямой 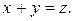 Величина этой площади зависит от значения
Величина этой площади зависит от значения 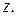
Если 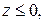 то
то 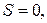 т.е.
т.е. 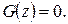
Если 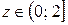 , то
, то 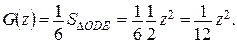
Если 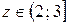 , то
, то 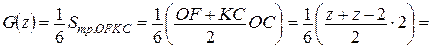
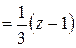 .
.
Если 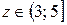 , то
, то 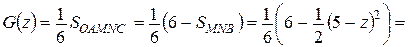
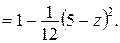
Если 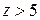 , то
, то 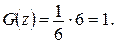
Итак, искомая функция распределения имеет вид
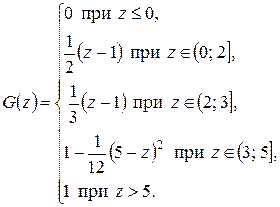
Найдем плотность распределения
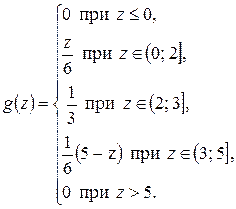
Построим график этой функции (рис. 10.2)
Рис. 10.2

 соответствует одно возможное значение случайной величины
соответствует одно возможное значение случайной величины 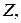 то
то 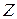 называют функцией двух случайных аргументов Х и
называют функцией двух случайных аргументов Х и 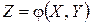 .
. дискретные независимые случайные величины, то для нахождения распределения функции
дискретные независимые случайные величины, то для нахождения распределения функции 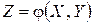 , надо найти все возможные значения
, надо найти все возможные значения  , и каждого возможного значения
, и каждого возможного значения  равного
равного 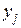 , вычислить значение
, вычислить значение 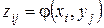 . Вероятности найденных возможных значений
. Вероятности найденных возможных значений  и
и  .
.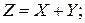 б)
б) 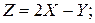 в)
в)  г)
г) 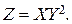
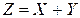
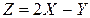
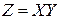
 2
2
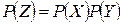
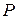
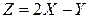
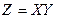

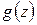 суммы
суммы 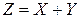 (при условии, что плотность распределения хотя бы одного из аргументов задана в интервале
(при условии, что плотность распределения хотя бы одного из аргументов задана в интервале  одной формулой) может быть найдена по формуле
одной формулой) может быть найдена по формуле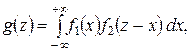
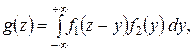
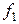 и
и 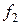 — плотности распределения аргументов.
— плотности распределения аргументов.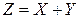 находят по формуле
находят по формуле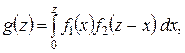
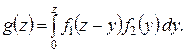
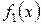 и
и 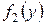 заданы на конечных интервалах, для отыскания плотности
заданы на конечных интервалах, для отыскания плотности 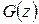 , а затем продифференцировать ее по
, а затем продифференцировать ее по 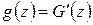 .
.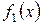 и
и 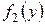 , то вероятность попадания случайной точки
, то вероятность попадания случайной точки 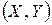 в область
в область 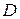 равна двойному интегралу по этой области от произведения плотностей распределения
равна двойному интегралу по этой области от произведения плотностей распределения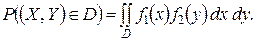
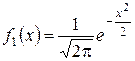 ,
, 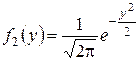 . Найти композицию этих законов, т.е. плотность распределения случайной величины
. Найти композицию этих законов, т.е. плотность распределения случайной величины 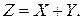
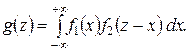 Тогда
Тогда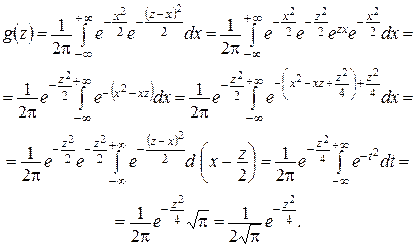
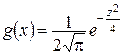 .
.
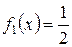 в интервале (0; 2), вне этого интервала
в интервале (0; 2), вне этого интервала  ,
, 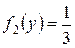 в интервале (0; 3), вне этого интервала
в интервале (0; 3), вне этого интервала  . Найти функцию распределения и плотность распределения случайной величины
. Найти функцию распределения и плотность распределения случайной величины 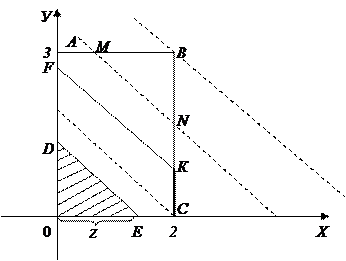 Решение. По условию, возможные значения Х определяются неравенством
Решение. По условию, возможные значения Х определяются неравенством 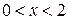 ,
, 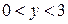 . Отсюда следует, что возможные случайные точки
. Отсюда следует, что возможные случайные точки 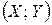 расположены в прямоугольнике ОАВС (рис. 10.1).
расположены в прямоугольнике ОАВС (рис. 10.1).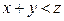 удовлетворяют те точки
удовлетворяют те точки 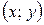 плоскости
плоскости  которые лежат ниже прямой
которые лежат ниже прямой 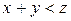 выполняется только для точек, лежащих в прямоугольнике ОАВС ниже прямой
выполняется только для точек, лежащих в прямоугольнике ОАВС ниже прямой 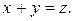 С другой стороны, так как величины Х и
С другой стороны, так как величины Х и 
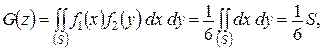
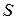 — величина той части площади прямоугольника ОАВС, которая лежит ниже прямой
— величина той части площади прямоугольника ОАВС, которая лежит ниже прямой 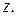
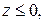 то
то 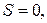 т.е.
т.е. 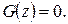
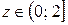 , то
, то 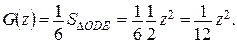
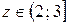 , то
, то 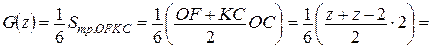
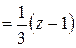 .
.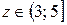 , то
, то 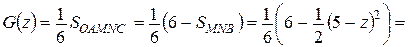
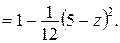
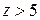 , то
, то