Задачи для самостоятельного решения. 9.1. Случайная величина Х распределена по следующему закону:
9.1. Случайная величина Х распределена по следующему закону:
Оценить вероятность того, что она примет значение, не превышающее 3, 6, пользуясь законом распределения и неравенством Маркова. Ответ:
9.2. Средний вес клубня картофеля равен 150 г. Оценить вероятность того, что наудачу взятый клубень картофеля весит не более 500 г? Ответ:
9.3. Среднее значение скорости ветра у земли в данном пункте равно 16 км/ч. Оценить вероятность того, что в этом пункте скорость ветра (при одном наблюдении) не превысит 80 км/ч. Ответ:
9.4. Среднее потребление электроэнергии за май населением одного из микрорайонов Минска равно 360 000 кВт/ч. Оценить вероятность того, что потребление электроэнергии в мае текущего года превзойдет 1 000 000 кВт/ч. Ответ: 9.5. Среднее квадратическое отклонение ошибки измерения курса самолета Ответ:
9.6. Среднее квадратическое отклонение ошибки измерения азимута равно Ответ: 9.7. Длина изготавливаемых деталей является случайной величиной, среднее значение которой 50 мм. Среднее квадратическое отклонение этой величины равно 0, 2 мм. Оценить вероятность того, что отклонение длины изготовленной детали от ее среднего значения по абсолютной величине не превзойдет 0, 4 мм. Ответ:
9.8. За значение некоторой величины принимают среднеарифметическое достаточно большого числа ее измерений. Предполагая, что среднее квадратическое отклонение возможных результатов каждого измерения не превосходит 5 мм, оценить вероятность того, что при 1000 измерений неизвестной величины отклонение принятого значения от истинного по абсолютной величине не превзойдет 0, 5 мм. Ответ:
9.9. Среднее квадратическое отклонение каждой из 450 000 независимых случайных величин не превосходит 10. Оценить вероятность того, что абсолютная величина отклонения среднеарифметической этих случайных величин от среднеарифметической их математических ожиданий не превзойдет 0, 02. Ответ:
9.10. Емкость изготовляемого заводом конденсатора по техническим условиям должна быть равной 2 мкф с разрешенным допуском ± 0, 1 мкф. Завод добился средней емкости, равной 2 мкф, с дисперсией, равной 0, 002 Ответ:
9.11. Выборочным путем требуется определить средний рост мужчин двадцатилетнего возраста. Какое количество мужчин, отобранных случайным образом, нужно измерить, чтобы с вероятностью, превышающей 0, 98, можно было утверждать, что средний рост у отобранной группы будет отличаться от среднего роста всех двадцатилетних мужчин по абсолютной величине не более чем на 1 см. Известно, что среднеквадратичное отклонение роста для каждого мужчины из отобранной группы не превышает 5 см. Ответ:
9.12. Технический контролер проверяет партию однотипных приборов. С вероятностью 0, 01 прибор имеет дефект А и, независимо от этого, с вероятностью 0, 02 — дефект В. В каких границах будет заключено практически наверняка число бракованных изделий в партии из 1000 шт., если за вероятность практической достоверности принимается 0, 997? Ответ:
9.13. Оценить вероятность того, что в партии из 5000 изделий отклонение частости бракованных деталей от вероятности 0, 02 быть бракованной деталью превысит 0, 01. Ответ:
9.14. Вероятность изготовления нестандартной радиолампы равна 0, 04. Какое наименьшее число радиоламп следует отобрать, чтобы с вероятностью 0, 88 можно было утверждать, что доля нестандартных радиоламп будет отличаться от вероятности изготовления нестандартной радиолампы по абсолютной величине не более чем на 0, 02? Ответ:
9.15. В рассматриваемом технологическом процессе в среднем 75 % изделий имеет допуск ± 5 %. Какое число изделий из партии в 200 000 шт. с вероятностью 0, 99 можно планировать с допуском ± 5 %? Ответ:
9.16. Произведено 500 независимых испытаний; в 200 из них вероятность появления события А была равна 0, 4, в 180 — 0, 5 и в 120 — 0, 6. Оценить снизу вероятность того, что отклонение частости от средней вероятности не превысит по абсолютной величине 0, 05. Ответ:
9.17. Стрельба ведется поочередно из трех орудий. Вероятности попадания в цель при одном выстреле из каждого орудия равны соответственно 0, 2; 0, 4; 0, 6. Таким образом произведено 600 выстрелов. Оценить снизу вероятность того, что отклонение частости от средней вероятности не превзойдет по абсолютной величине 0, 05. Ответ:
9.18. Из 5000 произведенных испытаний в 2000 вероятность появления события А равна 0, 2, в 1400 — 0, 5 и в 1600 — 0, 6. Найти границы, в которых должна находиться частость появления события А, если это необходимо гарантировать с вероятностью 0, 95. Ответ:
|



 .
. .
. Считая математическое ожидание ошибки измерения равным нулю, оценить вероятность того, что ошибка при данном измерении курса самолета будет более
Считая математическое ожидание ошибки измерения равным нулю, оценить вероятность того, что ошибка при данном измерении курса самолета будет более 

 (математическое ожидание равно нулю). Оценить вероятность того, что ошибка среднего арифметического трех независимых измерений не превзойдет 1°.
(математическое ожидание равно нулю). Оценить вероятность того, что ошибка среднего арифметического трех независимых измерений не превзойдет 1°. .
. .
. .
.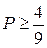 .
.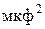 . Какой процент составляет вероятный брак при изготовлении конденсаторов? Расчет произвести по неравенству Чебышева и формуле Лапласа.
. Какой процент составляет вероятный брак при изготовлении конденсаторов? Расчет произвести по неравенству Чебышева и формуле Лапласа. .
. .
.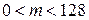 .
. .
. .
. .
. .
. .
. .
.


