Алгоритмы

1. Как называется графическое представление алгоритма:

1) последовательность формул; 2) блок-схема; 3) таблица; 4) словесное описание?

2. На рисунке представлена часть блок-схемы. Как называется такая вершина: ----- И

1) предикатная; 2) объединяющая; 3) функциональная; 4) сквозная?

3. На рисунке представлена часть блок-схемы. Как называется такая вершина:

1) предикатная;

2) объединяющая;

3) функциональная;

 

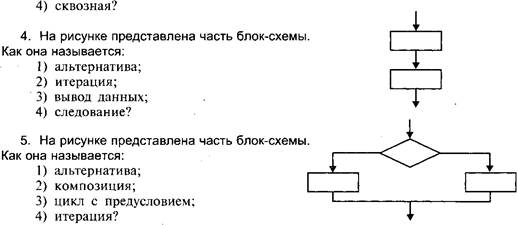
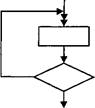
На рисунке представлена часть блок-схемы. Как она называется:

1) альтернатива;

2) композиция;

3) цикл с предусловием;

4) цикл с постусловием?

7. На рисунке представлена часть блок-схемы. Как она называется:

1) альтернатива;

2) композиция;

3) цикл с постусловием;

4) цикл с предусловием?

8. Как называется конструкция блок-схемы, изоб раженная на рисунке:

1) выполнение операций;

2) начало-конец алгоритма;

3) вызов вспомогательного алгоритма;

4) ввод/вывод данных?

9. Как называется конструкция блок-схемы, изоб­раженная на рисунке:

1) выполнение операций; -------------------

2) начало-конец алгоритма;

3) вызов вспомогательного алгоритма; -------------------

4) ввод/вывод данных?

10. Как называется конструкция блок-схемы, изоб­раженная на рисунке:

1) выполнение операций; гт ------------ г~

2) начало-конец алгоритма;

3) вызов вспомогательного алгоритма;

4) ввод/вывод данных?

11. Как называется конструкция блок-схемы, изоб­раженная на рисунке:

1) выполнение операций; /---------------- у

2) начало-конец алгоритма; / /

3) вызов вспомогательного алгоритма; ^----------------- '

4) ввод/вывод данных?

12. Свойство алгоритма записываться в виде упо­рядоченной совокупности отделенных друг от друга предписаний (директив):

1) понятность; 2) определенность; 3) дискретность; 4) массовость.

13. Свойство алгоритма записываться в виде только тех команд, которые находят­ся в Системе Команд Исполнителя, называется:

1) понятность; 2) определенность; 3) дискретность; 4) результативность.

14. Свойство алгоритма записываться только директивами однозначно и одинако­во интерпретируемыми разными исполнителями:

< сз>

1) детерминированность; 2) результативность; 3) дискретность; 4) понятность.

15. Свойство алгоритма, что при точном исполнении всех предписаний процесс должен прекратиться за конечное число шагов с определенным ответом на постав­ленную задачу:

1) понятность; 2) детерминированность; 3) дискретность; 4) результативность.

16. Свойство алгоритма обеспечения решения не одной задачи, а целого класса задач этого типа:

1) понятность; 2) определенность; 3) дискретность; 4) массовость.

17. Что называют служебными словами в алгоритмическом языке:

1) слова, употребляемые для записи команд, входящих в СКИ;

2) слова, смысл и способ употребления которых задан раз и навсегда;

3) вспомогательные алгоритмы, которые используются в составе других ал­горитмов;

4) константы с постоянным значением?

18. Рекурсия в алгоритме будет прямой, когда:

1) рекурсивный вызов данного алгоритма происходит из вспомогательного алгоритма, к которому в данном алгоритме имеется обращение;

2) порядок следования команд определяется в зависимости от результатов проверки некоторых условий;

3) команда обращения алгоритма к самому себе находится в самом алгоритме;

4) один вызов алгоритма прямо следует за другим.

19. Рекурсия в алгоритме будет косвенной, когда:

1) рекурсивный вызов данного алгоритма происходит из вспомогательного алгоритма, к которому в данном алгоритме имеется обращение;

2) порядок следования команд определяется в зависимости от результатов прбверки некоторых условий;

3) команда обращения алгоритма к самому себе находится в самом алгоритме;

4) один вызов алгоритма прямо следует за другим.

20. Команда машины Поста имеет структуру п К т, где:

1) п — действие, выполняемое головкой; К — номер следующей команды, подлежащей выполнению; т — порядковый номер команды;

2) п — порядковый номер команды; К — действие, выполняемое головкой; т — номер следующей команды, подлежащей выполнению;

3) п — порядковый номер команды; К— номер следующей команды, подле­жащей выполнению; т — действие, выполняемое головкой;

4) п — порядковый номер команды; К — действие, выполняемое головкой; т — номер клетки, с которой данную команду надо произвести.

21. Сколько существует команд у машины Поста: 1) 2; 2) 4; 3) 6; 4) 8?

22. В машине Поста останов будет результативным:

1) при выполнении недопустимой команды;

2) если машина не останавливается никогда;

3) если результат выполнения программы такой, какой и ожидался;

4) по команде «Стоп».

23. В машине Поста некорректным алгоритм будет в следующем случае:

1) при выполнении недопустимой команды;

2) результат выполнения программы такой, какой и ожидался;

3) машина не останавливается никогда;

4) по команде «Стоп».

24. В машине Тьюринга рабочий алфавит:

1) А = {а₄₀ О, Ь₄₀ 1, с₄₀ 2, щ₀ Г};

2) А = {а₄₀ 0, а₄₀ 1, а₄₀ 2,..., а₄₀ 7};

3) А = {а₄₀ О, я₄₁ 0, а₄₂ 0,..., а_4х О};

4) А = {а_ю О, а₂₀ О, а₃₀ О,..., а₉₀ О}.

25. В машине Тьюринга состояниями являются:

1) {а₄ о 0, а₄₀ 1, а₄₀ 2,..., а₄₀

2) {Яаь Я429 ЯАЪ

3) {#41, Я429 443, Я4& 9 «40 0, а₄₀ 1, а₄₀ 2,..., а₄₀

4) {? 40>? 4Ь #42, 04®} •

26. В машине Тьюринга предписание /_ для лентопротяжного механизма означает: 1) переместить ленту вправо; 2) переместить ленту влево;

3) остановить машину; 4) занести в ячейку символ.

27. В машине Тьюринга предписание для лентопротяжного механизма означает: 1) переместить ленту вправо; 2) переместить ленту влево;

3) остановить машину; 4) занести в ячейку символ.

28. В машине Тьюринга предписание 3 для лентопротяжного механизма означает: 1) переместить ленту вправо; 2) переместить ленту влево;

3) остановить машину; 4) занести в ячейку символ.

29. В алгоритме Маркова ассоциативным исчислением называется:

1) совокупность всех слов в данном алфавите;

2) совокупность всех допустимых систем подстановок;

3) совокупность всех слов в данном алфавите вместе с допустимой системой подстановок;

4) когда все слова в алфавите являются смежными.

30. В ассоциативном счислении два слова называются смежными:

1) если одно из них может быть преобразовано в другое применением под­становок;

2) если одно из них может быть преобразовано в другое однократным приме­нением допустимой подстановки;

3) когда существует цепочка от одного слова к другому и обратно;

4) когда они дедуктивны.

31. В алгоритме Маркова дана цепочка Р Р₁ Р₂... Р_к. Если слова Р_ь Р₂, Р_к-1 смежные, то цепочка называется:

1) ассоциативной;

2) эквивалентной;

3) индуктивной;

4) дедуктивной.

32. В алгоритме Маркова дана цепочка Р Р₁ Р₂... Р_к. Если слова Р_ь Р₂, Р^ смежные и цепочка существует и в обратную сторону, то слова РиР, называют:

1) ассоциативными;

2) эквивалентными;

3) индуктивными;

4) дедуктивными.

33. В алгоритмах Маркова дана система подстановок в алфавите А = {а, Ь, с}: аЬс — с

Ьа — сЬ са — аЬ

Преобразуйте с помощью этой системы слово ЬасааЬс:

1) сЬс\ 2) ссЬсЬЬс; 3) сЬасЬа; 4) сЬаЬс.

34.В алгоритмах Маркова дана система подстановок в алфавите А = {а, Ь, с}:

сЬ — аЬс

Ьас — ас

саЬ — Ь

Преобразуйте с помощью этой системы слово ЬсаЬасаЬ:

1) ссЬ\ 2) саЬ; 3) сЬс\ 4) ЬсааЬ.

35.Способ композиции нормальных алгоритмов будет суперпозицией, если:

1) выходное слово первого алгоритма является входным для второго;

2) существует алгоритм С, преобразующий любое слово р, содержащееся в пересечении областей определения алгоритмов А и В\

3) алгоритм В будет суперпозицией трех алгоритмов АБС, причем область определения В является пересечением областей определения алгоритмов А В и С, а для любого слова р из этого пересечения В(р) = А(р), если С(р) = е, В(р) = В(р)₃ если С(р) = е, где е — пустая строка;

4) существует алгоритм С, являющийся суперпозицией алгоритмов А и В, такой, что для любого входного слова р С(р) получается в результате последовательного многократного применения алгоритма А до тех пор, пока не получится слово, преобразуемое алгоритмом В.

36. Способ композиции нормальных алгоритмов будет объединением, если:

1) выходное слово первого алгоритма является входным для второго;

2) существует алгоритм С, преобразующий любое слово р, содержащееся в пересечении областей определения алгоритмов А и В;

3) алгоритм В будет суперпозицией трех алгоритмов А В С, причем область определения В является пересечением областей определения алгоритмов А В и С, а для любого слова р из этого пересечения В(р) = А(р), если С(р) = е, В(р) = В(р), если С(р) = е, где е — пустая строка;

4) существует алгоритм С, являющийся суперпозицией алгоритмов А и В, такой, что для любого входного слова р С(р) получается в результате последовательного многократного применения алгоритма А до тех пор, пока не получится слово, преобразуемое алгоритмом В.

37. Способ композиции нормальных алгоритмов будет разветвлением, если:

1) выходное слово первого алгоритма является входным для второго;

2) существует алгоритм С, преобразующий любое слово р, содержащееся в пересечении областей определения алгоритмов А и В;

3) алгоритм В будет суперпозицией трех алгоритмов А В С, причем область определения В является пересечением областей определения алгоритмов А В и С, а для любого слова р из этого пересечения В(р) = А(р), если С(р) = е, В(р) = В(р), если С(р) = е, где е — пустая строка;

4) существует алгоритм С, являющийся суперпозицией алгоритмов А и В, такой, что для любого входного слова р С(р) получается в результате последовательного многократного применения алгоритма А до тех пор, пока не получится слово, преобразуемое алгоритмом В.

38. Способ композиции нормальных алгоритмов будет итерацией, если:

1) выходное слово первого алгоритма является входным для второго;

2) существует алгоритм С, преобразующий любое слово р, содержащееся в пересечении областей определения алгоритмов А и В;

3) алгоритм В будет суперпозицией трех алгоритмов А В С, причем область определения В является пересечением областей определения алгоритмов А В и С, а для любого слова р из этого пересечения В(р) = А(р), если С(р) = е, В(р) = В(р), если С(р) = е, где е — пустая строка;

4) существует алгоритм С, являющийся суперпозицией алгоритмов А и В, такой, что для любого входного слова р С(р) получается в результате последовательного многократного применения алгоритма А до тех пор, пока не получится слово, преобразуемое алгоритмом В.