Аналитический расчет характеристик системы. множество состояний рассматриваемой двухфазной системы обслуживания будет следующим: {Si,j}={S0,0, S1,0
множество состояний рассматриваемой двухфазной системы обслуживания будет следующим: {Si, j}={S0, 0, S1, 0, S0, 1, S1, 1, Sb, 1}. Граф переходов системы показан на рис. 6. Система дифференциальных уравнений, описывающих поведение вероятностей состояний системы, здесь получается такой
Для стационарного режима работы получаем такую систему алгебраических уравнений:
к которым следует добавить нормировочное уравнение
Рисунок 6 – Граф переходов системы с блокировкой
Решение этой системы уравнений проведем следующим образом: Из (1) и (5) выразим переменные Р00 и Рb1:
Подставим (7) и (8) в оставшиеся уравнения:
Уравнение (10) исключим, т.к. переменных 3, а уравнений 4 (нормировочное уравнение (12) исключать нельзя):
Обозначим: A = B = C = В результате получаем:
Решение данной системы уравнений будем искать по правилу Крамера: P 01 = Здесь
Таким образом, получаем: · Вероятность того, что занят обслуживанием только первый прибор: P 10 = · Вероятность того, что занят обслуживанием только второй прибор: P 01 = · Вероятность того, что заняты оба прибора: P 11 = Вероятность того, что оба прибора свободны:
Вероятность блокировки первой фазы:
Определим относительную и абсолютную пропускные способности системы. Первый прибор отказывает заявке в обслуживании, если он занят обслуживанием другой заявки, а занят он в состояниях S10, S11 и Sb1, поэтому:
Абсолютная пропускная способность первого прибора равна:
Абсолютная пропускная способность первого прибора есть интенсивность потока заявок, поступающих на второй прибор. Второй прибор не принимает заявку, если он занят, однако заявка не покидает систему, а остается в первом приборе, что может привести к отказу очередной заявке, поступившей на вход первого прибора. Заявка, задержанная в первом приборе, покинет его, как только освободится второй прибор, т.е. все заявки, поступающие на вход второго прибора, будут обслужены, поэтому относительная пропускная способность этого прибора равна 1
Абсолютная пропускная способность второго прибора и системы в целом равна:
Подставим в полученные выражения значения параметров системы:
A = B = C =
P 01 = P 11 = P 00 = Pb 1 = P отк = 0.2484+0.0576+0.0651 = 0.3711, q 1 = 1 – 0.3711 = 0.6289, A 1 = 0.33*0.6289 = 0.2075, q 2 = 1, A 2 = 0.2075.
|


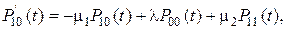



 , (1)
, (1) , (2)
, (2) , (3)
, (3) , (4)
, (4) , (5)
, (5) . (6)
. (6)
 , (7)
, (7) . (8)
. (8) , (9)
, (9) , (10)
, (10) . (12)
. (12) ,
, ,
, .
. ,
, ,
, .
.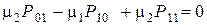 ,
, ,
, .
. , P 10 =
, P 10 =  , P 11 =
, P 11 =  .
. определитель системы
определитель системы
 =
=  ,
, определитель для P 01:
определитель для P 01:
 =
=  ,
, определитель для P 10:
определитель для P 10: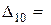
 =
=  ,
, определитель для P 11:
определитель для P 11:
 =
= 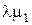 .
.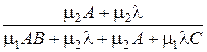 .
.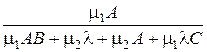 .
. .
. .
. .
. .
. .
. .
. .
. = 0.33,
= 0.33, 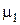 = 0.678,
= 0.678, 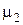 = 0.6.
= 0.6. ,
, ,
, ,
, ,
, ,
,


