Система с отказами
Имеется одноканальная двухфазная система массового обслуживания с отказами с разной производительностью приборов (рис. 1).
Рисунок 1 – Структурная схема системы с отказами
Обозначим состояния системы: S 00 – первый и второй приборы свободны от обслуживания; S 10 – первый прибор занят обслуживанием, второй свободен; S 01 – первый прибор свободен, второй занят обслуживанием; S 11 – оба прибора заняты обслуживанием. Граф переходов системы показан на рис. 2.
Рисунок 2 – Граф переходов системы с отказами
Система дифференциальных уравнений, описывающих поведение вероятностей состояний системы, получается такой
В стационарном режиме вероятности состояний системы постоянны, поэтому их производные равны нулю и система дифференциальных уравнений превращается в систему линейных алгебраических уравнений
к которым надо добавить нормировочное уравнение
Решение этой системы алгебраических уравнений проведем следующим образом. Прежде всего, упростим систему. Для этого из первого уравнения найдем P 00 и подставим полученное выражение во второе и последнее уравнения. Получаем
Замечаем, неизвестных 3, а уравнений 4, следовательно, одно уравнение можно исключить. Последнее нормировочное уравнение исключать нельзя, поэтому исключим второе уравнение, как наиболее сложное. Запишем систему уравнений в упорядоченном виде
Решение будем искать по правилу Крамера (через определители)
Здесь
Таким образом, получаем § Вероятность того, что занят обслуживанием только первый прибор
§ Вероятность того, что занят обслуживанием только второй прибор
§ Вероятность того, что заняты оба прибора
§ Вероятность того, что все приборы свободны от обслуживания, найдем из уравнения (1)
Определим относительную и абсолютную пропускные способности системы. Первый прибор отказывает заявке в обслуживании, если он занят обслуживанием другой заявки, а занят он в состояниях S 10 и S 11, поэтому q 1 = 1 – (P 10 + P 11). § Абсолютная пропускная способность первого прибора равна A 1 = § Абсолютная пропускная способность первого прибора есть интенсивность потока заявок, поступающих на второй прибор. Второй прибор занят в состояниях S 01 и S 11, поэтому q 2 = 1 – (P 01 + P 11). § Абсолютная пропускная способность второго прибора и системы в целом равна A 2 = A 1 q 2 = Анализ этого выражения позволяет сделать вывод о том, что производительность системы не зависит от распределения приборов по фазам. (Производительность системы определяется произведением q 1 q 2.) Это означает, что пропускная способность системы определяется ее ”слабым звеном”. Если производительность одной из фаз очень мала по сравнению с другими, то эта фаза и будет определять пропускную способность системы.
|




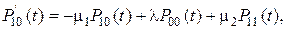


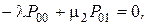




 (1)
(1)




 определитель системы
определитель системы = –
= –  ,
, определитель для P 10
определитель для P 10 =
= 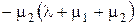 ,
, определитель для P 01
определитель для P 01 =
=  ,
, определитель для P 11
определитель для P 11 =
=  .
. .
. .
. .
. =
=  .
.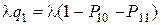 .
. q 1 q 2 =
q 1 q 2 = 


