Методические указания и решение типовых задач. При изучении данной темы необходимо обратить внимание на следующее: выявление роли и значения графических методов изображения статистических данных; освоение
При изучении данной темы необходимо обратить внимание на следующее: выявление роли и значения графических методов изображения статистических данных; освоение техники построения различных графических изображений; аналитическое значение графиков. При выявлении роли и значения графических методов изображения статистических данных необходимо обратить внимание на то, что графические методы в статистике являются способом наглядного изображения результатов статистической сводки и обработки массового материала. При правильном построении графики обладают выразительностью, доступностью, способствуют анализу явлений, их обобщению и изучению. В ряде случаев графики являются незаменимыми средствами анализа, исследования и выявления закономерностей статистических данных. При освоении техники построения различных графических изображений следует тщательно разобраться в различных методах построения графиков, что достаточно подробно изложено в учебнике. Главным в определении аналитического значения графиков является определение той формы графических изображений, которая дает наиболее наглядный аналитический результат. Несмотря на многообразие видов графических изображений, каждый график должен включать следующие элементы: графический образ; поле графика; масштабные ориентиры и систему координат. Графический образ – геометрические знаки, совокупность точек, линии, фигуры, с помощью которых изображаются статистические величины. Поле графика представляет собой пространство, в котором размещаются геометрические знаки. Масштабные ориентиры статистического графика определяются масштабом и масштабной шкалой. Масштаб статистического графика – это мера перевода числовой величины в графическую (рис. 5.1), а масштабная шкала – линия, определенные точки которой могут быть прочитаны как определенные числа. Шкала состоит из линии (носителя шкалы) и ряда помеченных на ней точек, расположенных в определенном порядке. Носитель шкалы может быть представлен прямой или кривой линией. Поэтому шкалы называются прямолинейными и криволинейными (круговые и дуговые).
Рис. 5.1. Масштабы
Шкалы могут быть равномерными и неравномерными (рис. 5.2). Одним из видов неравномерной шкалы является логарифмическая. На этой шкале отрезки пропорциональны не изображаемым величинам, а их логарифмам.
Рис.5.2. Масштабные шкалы: а) равномерные; б) неравномерные Для размещения геометрических знаков в поле графика необходима система координат. Наиболее распространенной при построении статистических графиков является система прямоугольных координат. При этом наилучшее соотношение масштаба по осям абсцисс и ординат 1, 62: 1, известное под названием «золотое сечение», а для других видов диаграмм нейтральным размером диаграммы является квадрат, получающийся из отношения 5/8, где 5 – высота площади диаграммы, а 8 – площадь его основания. Масштабом равномерной шкалы называется длина отрезка (графический интервал), принятого за единицу и измеренного в каких-либо мерах. Чем меньше масштаб (рис. 5.1), тем гуще располагаются на шкале точки, имеющие одно и то же значение. Построить шкалу – это значит на задуманном носителе шкалы разместить точки и обозначить их соответствующими числами согласно условиям задачи (рис. 5.3).
Рис. 5.3. Длина отрезка равномерной масштабной шкалы
Для наглядного изображения циклического изменения во времени строятся линейные графики в полярной системе координат. Они носят название радиальных диаграмм. В радиальных диаграммах радиусы обозначают периоды времени, а окружность - величину изучаемого явления (рис. 5.4).
Рис. 5.4. Числовые интервалы в полярной системе координат
На статистических картах пространственная ориентировка задается контурной сеткой, определяющей те территории, к которым относятся статистические характеристики. В результате изучения данной темы студенты должны научиться строить различные виды диаграмм, статистических карт и уяснить, что в диаграммах цифровые данные чаще всего изображаются в виде линий и геометрических фигур (плоскостных и объемных). В статистических картах цифровые данные изображаются путем нанесения на контурные географические карты условных знаков в виде точек, различной штриховки или раскраски, диаграммных знаков. Рассмотрим построение основных видов диаграмм на конкретных числовых примерах. На столбиковых диаграммах статистические данные изображаются в виде вытянутых по вертикали прямоугольников. При построении столбиковых диаграмм необходимо выполнять следующие требования: 1) шкала, по которой устанавливается высота столбика, должна начинаться с нуля; 2) шкала должна быть, как правило, непрерывной; 3) основания столбиков должны быть равны между собой; столбики могут быть размещены на одинаковом расстоянии друг от друга, вплотную один к другому или наплывом, при котором один столбик частично накладывается на другой; 4) наряду с разметкой шкалы соответствующими цифровыми надписями следует снабжать и сами столбцы. Например, изобразим графические данные о численности населения России за 1959 - 1997 гг., млн. чел.: 1959 г. – 117, 5; 1970 г. – 130, 1; 1979 г. – 137, 6; 1989 г. – 147, 4; 1990 г. – 148, 0; 1997 г. – 148, 0. На горизонтальной оси поместим основания шести столбиков на расстоянии 0, 5 см друг от друга. Ширина столбиков – 1 см. Масштаб на вертикальной оси – 10 млн.. чел. на 1 см (рис. 5.5).
 
Рис. 5.5.Численность населения России за 1959-1997 гг. Полосовые диаграммы состоят из прямоугольников, расположенных горизонтально (полосами, лентами). В этом случае масштабной шкалой будет горизонтальная ось. Принцип их построения тот же, что и столбиковых. В отличие от столбиковых или полосовых диаграмм в квадратных и круговых диаграммах величина изображаемого явления выражается размером площади. Чтобы построить квадратную диаграмму, необходимо из сравниваемых статистических величин извлечь квадратные корни, а затем построить квадраты со сторонами, пропорциональными полученным результатам. Например, необходимо построить квадратную диаграмму для сравнения грузооборотов железнодорожного, речного и автомобильного транспорта за 1997 г. (цифры условные). Для построения диаграммы нужно извлечь квадратные корни из следующих величин: грузооборот железнодорожного транспорта – 1195 млрд. т-км; грузооборот морского транспорта – 305; грузооборот внутреннего водного транспорта – 87 млрд. т-км. Это составит соответственно 34, 6: 17.5: 9, 3. Чтобы построить по этим данным квадраты, необходимо выбрать масштаб. Примем 1 см за 5 млрд. т-км. Сторонами квадратов на графике будут отрезки, пропорциональные полученным числам (рис. 5.6).
Рис. 5.6. Грузооборот некоторых видов транспорта в одном из регионов за 1997 г. Круговые диаграммы строятся аналогично. Разница состоит лишь в том, что на графике вычерчиваются круги, площади которых пропорциональны квадратным корням из изображаемых величин. Диаграммы фигур-знаков представляют собой графические изображения в виде рисунков, силуэтов, фигур, соответствующих содержанию статистических данных. Они отличаются от других видов диаграмм тем, что отдельные величины на них изображаются определенным количеством одинаковых по размеру и типу фигур. Например, для изображения динамики производства стиральных машин в России один рисунок условно примем за 700 тыс. шт. стиральных машин. Тогда число машин: в 1993 г. в размере 5877 тыс. шт. должно быть изображено в количестве 5, 5 рисунка: в 1994 г. в размере 2107 тыс. шт. – 3, 0 рисунка; в 1995 г. в размере 1293 тыс. шт. – 1, 8 рисунка; в 1996 г. в размере 761 тыс. шт. – 1, 01 рисунка (рис. 5.7).
Рис.5.7. Динамика производства стиральных машин в России в 1993-1996 гг.
Секторные диаграммы удобно строить следующим образом: вся величина явления принимается за 100%, рассчитываются доли отдельных его частей в процентах. Круг разбивается на секторы пропорционально частям изображаемого целого. Таким образом, на 1% приходится 3, 6°. Для получения центральных углов секторов, изображающих доли частей целого, необходимо их процентное выражение умножить на 3, 6°. Например, изобразим графически данные о структуре валового внутреннего продукта по видам первичных доходов (в текущих ценах) России за 1994 и 1995 гг.: в 1994 г. оплата труда наемных работников 41, 0%, валовая прибыль экономики и валовые смешанные доходы 50, 0, чистые налоги на производство и импорт 9%; в 1995 г. соответственно 33, 0%; 57, 0 и 10, 0%. Построим два круга одинакового радиуса. По данным о структуре валового внутреннего продукта для построения секторов определим центральные углы: для 1994 г. центральные углы составили 147, 6° (41, 0·3, 6); 180, 0° (50, 0·3, 6); 32, 4° (9, 0·3, 6); для 1995 г. – 118, 8° (33, 0·3, 6); 205, 2° (57, 0·3, 6); 36° (10, 0·3, 6). При помощи транспортира разделим круги на соответствующие секторы (рис. 5.8).
Рис. 5.8. Структура валового внутреннего продукта по видам первичных доходов (в текущих ценах)
Если данные о структуре какого-либо явления выражаются в абсолютных величинах, то для нахождения секторов необходимо 360° разделить на величину целого, а затем частное от деления последовательно умножить на абсолютные значения частей. Для одновременного сопоставления трех величин, связанных между собой таким образом, что одна величина является произведением двух других, применяют диаграммы, называющиеся «знак Варзара». Знак Варзара представляет собой прямоугольник, у которого один сомножитель принят за основание, другой – за высоту, а вся площадь равна произведению. Например, произведение посевной площади и урожайности дает валовой сбор. Если в прямоугольнике одну сторону брать пропорционально посевной площади, а другую – урожайности, то площадь прямоугольника и представляет собой знак Варзара, т.е. валовой сбор. Линейные диаграммы широко применяются для характеристики изменений явлений во времени, выполнения плановых заданий, а также для изучения рядов распределения, выявления связи между явлениями. Линейные диаграммы строятся на координатной сетке. Геометрическими знаками в линейных диаграммах служат точки и последовательно соединяющие их отрезки прямой, которые складываются в ломаные кривые. Например, при помощи линейной диаграммы можно изобразить данные о производстве легковых автомобилей за 1992-1997 гг., тыс. шт. (цифры условные). 1992 1993 1994 1995 1996 1997 344 529 730 917 1100 1200 В прямоугольной системе координат нанесем на ось абсцисс показатели времени, а на ось ординат – данные о производстве автомобилей (рис. 5.9). Масштаб – 1 см = 200 тыс. шт. Из графика видно, что положение кривой определяется не только данными о производстве автомобилей, но и интервалами времени между датами. Нередко на одной линейной диаграмме приводятся несколько кривых, которые дают сравнительную характеристику динамики различных показателей или одного и того же показателя для разных территорий. Методика построения таких кривых не отличается от построения графика на рис. 5.9.
Рис.5.9. Динамика производства легковых автомобилей в одном из регионов за 1992-1997 гг. Ряды распределения чаще всего изображаются в виде полигона или гистограммы. Полигон строят в основном для изображения дискретных рядов. При его построении на оси абсцисс откладываются значения варьирующего признака, а на оси ординат – абсолютные или относительные численности единиц совокупности (частоты или частости). Полигон на рис. 5.10 построен на основании (условных) данных о распределении семей по числу детей.
Рис. 5.10. Полигон распределения семей по числу детей в одном из регионов в 1997 г. (цифры условные)
Гистограмма распределения применяется чаще всего для изображения интервальных рядов. Для ее построения по оси абсцисс откладываются интервалы признака, а по оси ординат – численности единиц совокупности. На отрезках, изображающих интервалы, строят прямоугольники, площади которых пропорциональны численностям единиц (рис. 5.11).
Рис. 5.11. Гистограмма распределения заводов в одной из отраслей по стоимости основных производственных фондов в 1997 г. (цифры условные) В ряде случаев для изображения вариационных рядов используется кумулятивная кривая (кумулята). Для ее построения значения варьирующего признака откладываются на оси абсцисс, а на оси ординат помещаются накопленные итоги частот или частостей (рис. 5.12).
Рис. 5.12. Кумулята распределения семей по числу детей в одном из регионов в 1997 г. (цифры условные)
Если поместить на оси абсцисс накопленные частоты, а на оси ординат нарастающие итоги значений группировочного признака, то в этом случае мы получим кривую, называемую кривой концентрации (глава 11). Для графического изображения взаимосвязи между явлениями на оси абсцисс необходимо поместить значения признака-фактора, а на оси ординат – значения признака-результата (рис. 9.1, глава 9). Разновидностью линейной диаграммы является радиальная диаграмма, которая применяется для изображения рядов динамики при наличии в них сезонных колебаний. Построение радиальной диаграммы разберем на следующем примере. Имеются данные (условные) о продаже творога на колхозных рынках одного из городов региона в 1997 г.:
Определим среднемесячную продажу творога. Она составляет 43, 3 т. Вычертим круг с радиусом, равным среднемесячному показателю (R = 43, 3 т). На горизонтальном диаметре построим шкалу, взяв длину радиуса, равную 2, 7 см. Следовательно,
Рис. 5.13. Продажа творога на колхозных рынках в одном из городов в 1997 г.
Картограммы делятся на фоновые и точечные. Например, с помощью фоновой картограммы можно изобразить плотность населения на 1 км2 по областям страны. При построении точечной картограммы графическим изображением статистических данных являются точки, размещенные в пределах территориальных единиц. Принцип построения картодиаграммы заключается в том, что на контурной карте составные части какой-либо диаграммы размещаются на площади, отведенной определенному территориальному подразделению страны (а на картах мира или частей света – определенной стране). Например, если необходимо построить картодиаграмму производства кирпича по областям России за 1997 г. с использованием столбиковой диаграммы, то надо столбик, высота которого отражает объем производства кирпича в данной области, разместить на том месте, которое отведено для нее на карте. Выбирая масштаб, нужно следить за тем, чтобы столбики не выходили за пределы своих областей.
|




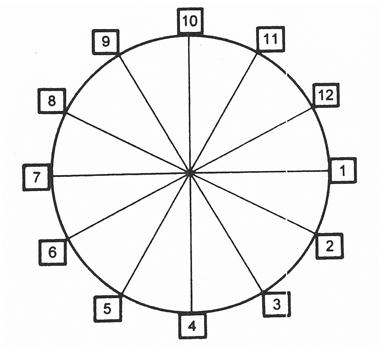







 . Затем весь круг разделим на 12 радиусов (соответственно числу месяцев в году). На радиусе сделаем отметку согласно масштабу исходя из приведенных данных за каждый месяц. Данные, которые превысили среднемесячный уровень, отмечаются за пределами окружности на продолжении радиуса. Отметки различных месяцев соединяются между собой (рис. 5.13).
. Затем весь круг разделим на 12 радиусов (соответственно числу месяцев в году). На радиусе сделаем отметку согласно масштабу исходя из приведенных данных за каждый месяц. Данные, которые превысили среднемесячный уровень, отмечаются за пределами окружности на продолжении радиуса. Отметки различных месяцев соединяются между собой (рис. 5.13).



