Методические указания и решение типовых задач. Исследование вариации в статистике и социально-экономических исследованиях имеет важное значение, так как величина вариации признака в статистической
Исследование вариации в статистике и социально-экономических исследованиях имеет важное значение, так как величина вариации признака в статистической совокупности характеризует ее однородность. В статистической практике для изучения и измерения вариации используются различные показатели (меры) вариации в зависимости от поставленных перед исследователем задач. К ним относятся размах вариации, среднее линейное отклонение, средний квадрат отклонений (дисперсия), среднее квадратическое отклонение и коэффициент вариации. При изучении вопроса о вариации нужно четко представлять себе условия, порождающие вариацию признаков, а также сущность и значение измерения вариации признаков. Следует также усвоить, что изучение вариации признаков общественных явлений находится в прямой связи с группировками, в частности с рядами распределения. Очень важно научиться свободно исчислять все показатели вариации. Способы вычисления показателей вариации. Размах вариации (R) является наиболее простым измерителем вариации признака. R = xmax – xmin, где хmax – наибольшее значение варьирующего признака; хmin – наименьшее значение признака. Среднее линейное отклонение (
Символы хi, Пример. На основе данных табл. 7.1 рассчитаем среднее линейное отклонение для дискретного ряда распределения. Решение. Размах вариации стажа равен: R = 12 – 8 = 4 года. Результаты вспомогательных расчетов даны в графах 3-5 табл. 7.1. Средний стаж работы определяем по формуле средней арифметической взвешенной:
Отклонения индивидуальных значений стажа от средней с учетом и без учета знака содержатся в графах 4 и 5, а произведения отклонений по модулю на соответствующие частоты – в гр. 6. Таблица 7.1 Распределение учителей средних школ района по стажу работы
Среднее линейное отклонение стажа работы учителей средних школ района
Показатели дисперсии и среднего квадратического отклонения являются общепринятыми мерами вариации и широко используются в статистических исследованиях. Дисперсия представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины (обозначается греческой буквой σ 2 – «сигма квадрат»). Дисперсия вычисляется по формулам простой невзвешенной и взвешенной:
Среднее квадратическое отклонение представляет собой корень второй степени из среднего квадрата отклонений отдельных значений признака от их средней:
Среднее квадратическое отклонение – величина именованная, имеет размерность осредняемого признака. Пример. Рассчитаем дисперсию и среднее квадратическое отклонение для следующего ряда распределения (табл. 7.2).
Таблица 7.2 Распределение магазинов города по товарообороту во II квартале 1998 г.
Решение. В приведенных ранее примерах мы имели дело с дискретными рядами. При расчете показателей вариации по интервальным рядам распределения (табл. 7.2) необходимо сначала определить середины интервалов, а затем вести дальнейшие расчеты, рассматривая ряд середин интервалов как дискретный ряд распределения. Результаты вспомогательных расчетов для определения дисперсии и среднего квадратического отклонения содержатся в графах 2-6 табл. 7.2. Средний размер товарооборота определяется по средней арифметической взвешенной и составляет:
Дисперсия товарооборота
Среднее квадратическое отклонение товарооборота определяется как корень квадратный из дисперсии:
Расчет дисперсии прямым способом в ряде случаев трудоемок, поэтому логично, используя свойства дисперсии, упростить ее вычисления, например используя расчет дисперсии по способу отчета от условного нуля или способу моментов по следующей формуле:
С использованием начальных моментов формула расчета дисперсии по способу моментов имеет следующий вид: σ 2= k2 (m2 – m12), где k – величина интервала; А – условный нуль, в качестве которого удобно использовать середину интервала с наибольшей частотой;
В случае когда А приравнивается к нулю и, следовательно, не вычисляются отклонения, формула принимает вид:
Воспользуемся данными предыдущего примера и рассчитаем дисперсию по способу отсчета от условного нуля и способу моментов. Расчет произведем в табличной форме (табл. 7.3).
Таблица 7.3 Расчет дисперсии способом отчета от условного нуля
По способу отсчета от условного нуля:
По способу моментов получаем:
По способу разности между средней квадратов вариантов признака и квадратом их средней величины
Результаты расчетов дисперсии по всем трем способам дают одну и ту же величину. Для целей сравнения колеблемости различных признаков в одной и той же совокупности или же при сравнении колеблемости одного и того же признака в нескольких совокупностях вычисляются относительные показатели вариации. Базой для сравнения служит средняя арифметическая. Эти показатели вычисляются как отношение размаха, или среднего линейного отклонения, или среднего квадратического отклонения к средней арифметической. Чаще всего, они выражаются в процентах и характеризуют не только сравнительную оценку вариации, но и дают характеристику однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33% (для распределений, близких к нормальному). Различают следующие относительные показатели вариации (V): Коэффициент осцилляции: Линейный коэффициент вариации: Коэффициент вариации: Рассмотрим примеры определения этих показателей. По данным табл. 7.1, коэффициент осцилляции Коэффициент вариации вычислим на основе ряда распределения, представленного в табл. 7.2: Наиболее часто в практических расчетах из этих трех показателей применяется коэффициент вариации. Статистическое изучение вариации многих социально-экономических явлений проводится и при помощи дисперсии альтернативного признака. Обозначим наличие данного признака 1, отсутствие 0, долю вариантов, обладающих данным признаком, р, а не обладающих им q. Так как ряд р + q = 1, то средняя Определим дисперсию альтернативного признака по следующим данным: налоговой инспекцией одного из районов города проверено 172 коммерческих киоска и в 146 обнаружены финансовые нарушения. Тогда n = 172, m = 146; Наряду с изучением вариации признака по всей совокупности в целом часто бывает необходимо проследить количественные изменения признака по группам, на которые разделяется совокупность, а также и между группами. Такое изучение вариации достигается посредством вычисления и анализа различных видов дисперсии.
|

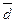 ) представляет собой среднюю величину из отклонений вариантов признака от их средней. Его можно рассчитать по формуле средней арифметической, как невзвешенной, так и взвешенной, в зависимости от отсутствия или наличия частот в ряду распределения:
) представляет собой среднюю величину из отклонений вариантов признака от их средней. Его можно рассчитать по формуле средней арифметической, как невзвешенной, так и взвешенной, в зависимости от отсутствия или наличия частот в ряду распределения: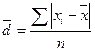 – невзвешенное среднее линейное отклонение;
– невзвешенное среднее линейное отклонение;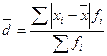 – взвешенное среднее линейное отклонение.
– взвешенное среднее линейное отклонение.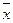 , fi и n имеют то же значение, что и в предыдущей главе. Рассмотренные выше показатели имеют ту же размерность, что и признак, для которого они вычисляются.
, fi и n имеют то же значение, что и в предыдущей главе. Рассмотренные выше показатели имеют ту же размерность, что и признак, для которого они вычисляются.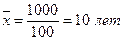
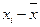

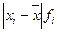
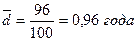
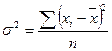 – невзвешенная;
– невзвешенная; – взвешенная.
– взвешенная.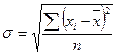 – невзвешенное;
– невзвешенное;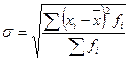 – взвешенное.
– взвешенное.
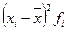


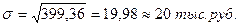
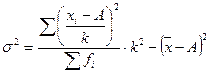
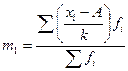 – начальный момент первого порядка;
– начальный момент первого порядка;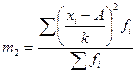 – начальный момент второго порядка.
– начальный момент второго порядка.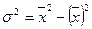 или
или 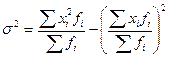
 (k = 10)
(k = 10)
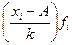

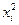
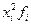
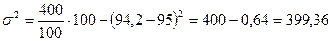

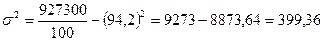
 .
.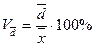 .
. .
.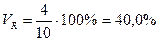 , а линейный коэффициент вариации
, а линейный коэффициент вариации 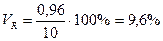 .
.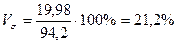 .
.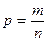 , n – число наблюдений, m – число единиц совокупности, обладающее данным признаком, q = 1 – р.
, n – число наблюдений, m – число единиц совокупности, обладающее данным признаком, q = 1 – р.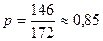 ; q = 1 – 0, 85 = 0, 15; σ 2 = 0, 85 · 0, 15 = 0, 1275.
; q = 1 – 0, 85 = 0, 15; σ 2 = 0, 85 · 0, 15 = 0, 1275.


