Задачи и упражнения. 7.1.Распределение студентов одного из факультетов по возрасту характеризуется следующими данными:
7.1. Распределение студентов одного из факультетов по возрасту характеризуется следующими данными:
Вычислите: а) размах вариации; б) среднее линейное отклонение; в) дисперсию; г) среднее квадратическое отклонение; д) относительные показатели вариации возраста студентов. 7.2. Определите среднюю длину пробега автофургона торгово-посреднической фирмы и вычислите все показатели вариации, если известны:
7.3. Имеется следующий ряд распределения телеграмм, принятых отделением связи, по числу слов:
Рассчитайте абсолютные и относительные показатели вариации. 7.4. Средняя урожайность зерновых культур в двух районах за 1991-1995 гг. характеризуется следующими данными, ц/га:
Рассчитайте все показатели вариации. Определите, в каком районе урожайность зерновых культур более устойчива. 7.5. Имеются следующие данные выборочного обследования студентов одного из вузов:
Вычислите абсолютные и относительные показатели вариации. 7.6. Имеются следующие данные о распределении скважин в одном из районов бурения по глубине:
Определите дисперсию и среднее квадратическое отклонение глубины скважин, применяя способ моментов и отсчета от условного нуля. 7.7. Акционерные общества области по среднесписочной численности работающих на 1 января 1998 г. распределялись следующим образом:
Рассчитайте: а) среднее линейное отклонение; б) дисперсию; в) среднее квадратическое отклонение; г) коэффициент вариации. 7.8. По данным о распределении сельских населенных пунктов по числу дворов вычислите общую дисперсию тремя способами: а) обычным; б) упрощенным; в) по формуле
7.9. Имеются следующие данные о распределении сотрудников коммерческого банка по среднемесячной заработной плате:
Определите общую дисперсию тремя способами: а) обычным; б) упрощенным; в) по формуле 7.10. Средняя величина признака в совокупности равна 19, а средний квадрат индивидуальных значений этого признака – 397. Определите коэффициент вариации. 7.11. Дисперсия признака равна 9, средний квадрат индивидуальных его значений – 130. Чему равна средняя? 7.12. Средняя величина в совокупности равна 16, среднее квадратическое отклонение – 8. Определите средний квадрат индивидуальных значений этого признака. 7.13. Средний квадрат отклонений индивидуальных значений признака от их средней величины равен 100, а средняя – 15. Определите, чему равен средний квадрат отклонений индивидуальных значений признака от величины, равной 10 и 25. 7.14. Средняя величина признака равна 14, а дисперсия – 60. Определите средний квадрат отклонений вариантов признака от 19. 7.15. Средний квадрат отклонений вариантов признака от произвольной величины равен 300, а сама произвольная величина равна 70 единицам. Определите дисперсию признака, если известно, что средняя величина его варианта равна 80. 7.16. Средний квадрат отклонений вариантов признака от некоторой произвольной величины равен 61. Средняя величина признака больше произвольной величины на 6 единиц и равна 10. Найдите коэффициент вариации. 7.17. Если дисперсия равна 20 000 единицам, а коэффициент вариации – 30%, то каков будет средний квадрат отклонений индивидуальных значений признака от величины, равной 250 единицам? 7.18. По данным таблицы о распределении пряжи по крепости нити вычислите все виды дисперсий. Определите общую дисперсию по правилу сложения дисперсий.
7.19. Товарооборот по предприятиям общественного питания на одного работника за квартал характеризуется следующими данными:
Определите все виды дисперсий товарооборота предприятий общественного питания. 7.20. Имеются данные о распределении семей сотрудников финансовой корпорации по количеству детей:
Вычислите: а) внутригрупповые дисперсии; б) среднюю из внутригрупповых дисперсий; в) межгрупповую дисперсию; г) общую дисперсию. Проверьте правильность произведения расчетов с помощью правила сложения дисперсий. 7.21. Распределение основных фондов по малым предприятиям отрасли характеризуется следующими данными:
Рассчитайте коэффициент детерминации и эмпирическое корреляционное отношение. Сделайте выводы. 7.22. Имеются следующие данные, характеризующие фермерские хозяйства региона:
Определите коэффициент детерминации и эмпирическое корреляционное отношение при условии, что посевные площади под зерновыми культурами во всех хозяйствах одинаковы. Сделайте выводы. 7.23. Распределение стоимости продукции, предназначенной для экспортных поставок, по цехам предприятия представлено следующими данными:
Вычислите: а) среднюю из внутригрупповых, межгрупповую и общую дисперсию дисперсии доли экспортной продукции; б) коэффициент детерминации и эмпирическое корреляционное отношение. 7.24. Имеются данные о распределении семей города по числу детей.
Используя центральные моменты первых четырех порядков, рассчитайте коэффициенты асимметрии и эксцесса. Сделайте выводы. 7.25. Распределение магазинов по размеру товарооборота за октябрь 1996 г. характеризуется следующими данными:
Определите показатели асимметрии и эксцесса распределения магазинов по размеру товарооборота. Сделайте выводы. 7.26. При исследовании трудовой активности сотрудников организации (отработано человеко-дней за год) получены средние величины и центральные моменты:
Используя показатели асимметрии и эксцесса, сравните характер распределения мужчин и женщин по трудовой активности. Сделайте выводы. 7.27. По данным выборочных обследований домашних хозяйств получены средние величины и центральные моменты:
На основе показателей асимметрии и эксцесса сравните характер распределения домашних хозяйств по годичному заработку главы семьи и среднедушевому доходу. Сделайте выводы. 7.28. Распределение 1000 семей по уровню душевого дохода за месяц характеризуется следующими данными:
На основе критерия χ 2 проверьте, согласуется ли распределение семей по среднедушевому доходу с нормальным или логарифмически-нормальным распределением с вероятностью 0, 95. 7.29. По данным задачи 7.28 проверьте близость эмпирического и теоретического распределений с помощью критериев Романовского и Колмогорова. 7.30. Результаты экзамена по теории статистики в одной из студенческих групп представлены в таблице:
Найдите модальный и медианные баллы успеваемости студентов. 7.31. При изучении качества семян пшеницы было получено следующее распределение семян по проценту всхожести:
Рассчитайте моду и медиану. 7.32. Вычислите моду и медиану количественного состава семей города на основании следующего их распределения по числу совместно проживающих членов семьи:
7.33. С целью исследования качества деталей на предприятии проверена партия из 100 деталей. Результаты представлены в следующей таблице:
Определите моду, медиану, квартили и децили. 7.34. По нижеследующим данным вычислите моду, медиану и квартили.
7.35. Рассчитайте моду, медиану, квартили и децили по данным задачи 7.25. 7.36. Определите моду, медиану, квартили и децили по данным задачи 7.28.
|

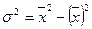 .
.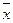
 Центральные
Центральные  моменты
моменты 




