Правило сложения дисперсий.Если данные представлены в виде аналитической группировки, то можно вычислить дисперсию общую, межгрупповую и внутригрупповуюОбщая дисперсия измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловливающих эту вариацию:
Межгрупповая дисперсия характеризует систематическую вариацию, т.е. различия в величине изучаемого признака, возникающие под влиянием признака-фактора, положенного в основание группировки. Она рассчитывается по формуле:
где хi и ni – соответственно средние и численности по отдельным группам Внутригрупповая дисперсия отражает случайную вариацию, т.е. часть вариации, происходящую под влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Она исчисляется следующим образом:
Средняя из внутригрупповых дисперсий
Существует закон, связывающий три вида дисперсий. Общая дисперсия равна сумме средней из внутригрупповых и межгрупповых дисперсий:
Данное соотношение называют правилом сложения дисперсий. Согласно этому правилу общая дисперсия, возникающая под влиянием всех факторов, равна сумме дисперсий, возникающих под влиянием всех прочих факторов, и дисперсии, возникающей за счет группировочного признака. Зная любые два вида дисперсий, можно определить или проверить правильность расчета третьего вида. Пример. Определим групповые дисперсии, среднюю из групповых дисперсий, межгрупповую дисперсию, общую дисперсию по данным табл. 7.4. Таблица 7.4 Производительность труда двух бригад рабочих-токарей
Решение. Для расчета групповых дисперсий вычислим средние по каждой группе:
Промежуточные расчеты дисперсий по группам представлены в табл. 7.4. Подставив полученные значения в формулу, получим:
Средняя из групповых дисперсий
Затем рассчитаем межгрупповую дисперсию. Для этого предварительно определим общую среднюю как среднюю взвешенную из групповых средних:
Теперь определим межгрупповую дисперсию:
Таким образом, общая дисперсия по правилу сложения дисперсий
Проверим полученный результат, исчислив общую дисперсию обычным способом:
На основании правила сложения дисперсий можно определить показатель тесноты связи между группировочным (факторным) и результативным признаками. Он называется эмпирическим корреляционным отношением, обозначается η («эта») и рассчитывается по формуле Величина 0, 86 характеризует существенную связь между группировочным и результативным признаками. Наряду с вариацией индивидуальных значений признака вокруг средней может наблюдаться и вариация индивидуальных долей признака вокруг средней доли. Такое изучение вариации достигается посредством вычисления и анализа следующих видов дисперсий. Внутригрупповая дисперсия доли определяется по формуле
Средняя из внутригрупповых дисперсий
Формула межгрупповой дисперсии имеет вид:
где ni – численность единиц в отдельных группах; р – доля изучаемого признака во всей совокупности, которая определяется по формуле
Общая дисперсия имеет вид:
Три вида дисперсии связаны между собой следующим образом:
Данное соотношение дисперсий называется теоремой сложения дисперсии доли признака. Эта теорема широко используется в изучении колеблемости качественных признаков. Пример. Определим групповые дисперсии, среднюю из групповых, межгрупповую и общую дисперсии по данным табл. 7.5.
Таблица 7.5 Численность и удельный вес одной из категорий крупного рогатого скота фермерских хозяйств района
Решение. Определим долю дойных коров в целом по трем хозяйствам:
Общая дисперсия доли дойных коров:
Внутригрупповые дисперсии:
Средняя из внутригрупповых дисперсий:
Межгрупповая дисперсия:
Используя правило сложения дисперсий, получаем: 0, 1025 + 0, 0031 = 0, 1056. Пример решен правильно. Выяснение общего характера распределения предполагает не только оценку степени его однородности, но и оценку его симметричности, остро- или плосковершинности. Симметричным называется распределение, в котором частоты любых двух вариантов, равноотстоящих в обе стороны от центра распределения, равны между собой. В статистике для характеристики асимметрии пользуются несколькими показателями. Показатели асимметрии и эксцесса. Степень асимметрии может быть определена с помощью коэффициента асимметрии:
где Мо – мода; σ – среднее квадратическое отклонение При симметричном (нормальном) распределении Если As < 0, то В практических расчетах часто в качестве показателя асимметрии применяется отношение центрального момента третьего порядка к среднему квадратическому отклонению данного ряда в кубе, т.е. Это дает возможность определить не только величину асимметрии, но и проверить наличие асимметрии в генеральной совокупности. Принято считать, что асимметрия выше 0, 5 (независимо от знака) считается значительной. Асимметрия меньше 0, 25 – незначительная. Пример. Рассчитаем коэффициент асимметрии по данным о распределении фирм по стоимости основных фондов (табл. 7.6). Таблица 7.6 Расчет коэффициента асимметрии
Решение. Определяем условные моменты m1, m2и m3, а также центральные моменты μ 2 и μ 3, необходимые для вычисления коэффициента асимметрии:
Коэффициент асимметрии для данного ряда
Полученный результат свидетельствует о наличии незначительной правосторонней асимметрии. Для симметричных распределений может быть также рассчитан показатель эксцесса:
При симметричном распределении Ek = 0. Если Ek > 0, распределение является островершинным; если Ek < 0 - плосковершинным. Вычислим Ek по данным табл. 7.6, определив вначале величину четвертого центрального момента: Оценка существенности показателей асимметрии и эксцесса позволяет сделать вывод о том, можно ли отнести данное эмпирическое распределение к типу нормального распределения. Построение нормального распределения по эмпирическим данным.Имея дело с эмпирическим распределением, можно предположить, что данному распределению соответствует определенная, характерная для него теоретическая кривая. Выдвинув гипотезу о той или иной форме распределения, стремятся описать эмпирический ряд с помощью математической модели, выражающей некоторый теоретический закон распределения. Среди различных кривых распределения особое место занимает нормальное распределение. Нормальное распределение чаще всего выражается следующей стандартизованной кривой нормального распределения:
где уt – ордината кривой нормального распределения;
е и π – математические постоянные: хi – значения изучаемого признака,
σ – среднее квадратическое отклонение изучаемого признака. Как видно из уравнения, два параметра – средняя арифметическая ( Пример. Рассчитаем значения частот теоретического ряда распределения на основании эмпирических данных об урожайности зерна в 500 фермерских хозяйствах, представленных в табл. 7.7. Таблица 7.7 Расчет теоретических частот нормального распределения
Продолжение таблицы 7.7
Для данного эмпирического распределения находим сначала значения Затем находим отклонения хi – Так как величина Критерии согласия. Количественная характеристика соответствия может быть получена с помощью особых статистических показателей-критериев согласия. Известны критерии согласия К. Пирсона (хи-квадрат), В.И. Романовского, Б.С. Ястремского и А.Н. Колмогорова. Критерий согласия Пирсона (χ 2) вычисляется по формуле
где fЭ и fT – эмпирические и теоретические частоты соответственно. С помощью величины χ 2 по специальным таблицам приложения определяется вероятность Р (χ 2). Входами в таблицу являются значения χ 2 и число степеней свободы γ = n – 1. На основе Р выносится суждение о существенности расхождения между эмпирическим и теоретическим распределениями. При Р > 0, 5 считается, что эмпирическое и теоретическое распределения близки. При РÎ (0, 2; 0, 5) совпадение между ними удовлетворительное, в остальных случаях недостаточное. Критерий Романовского (С), также используемый для проверки близости эмпирического и теоретического распределений, определяется следующим образом:
где χ 2 – критерий Пирсона: γ – число степеней свободы. При С < 3 различие несущественно, что позволяет считать эмпирическое распределение близким к нормальному. Критерий Ястремского (L) может быть найден на основе следующего соотношения:
где N – объем совокупности: pq – дисперсия альтернативного признака; k – число вариантов или групп; Q – принимает значение 0, 6, при числе вариантов или групп от 8 до 20. Если L < 3, то эмпирическое распределение соответствует теоретическому. Критерий Колмогорова (λ) вычисляется по формуле
где D – максимальное значение разности между накопленными эмпирическими и теоретическими частотами; Σ f – сумма эмпирических частот. Необходимым условием использования этого критерия является достаточно большее число наблюдений (не меньше ста). Пример. Рассчитаем критерии Колмогорова и Пирсона по данным табл. 7.8. Таблица 7.8 Расчет критерия Колмогорова по данным об урожайности зерновых в 500 фермерских хозяйствах
Как видно из табл. 7.8, максимальное значение разности между эмпирическими и теоретическими частотами составляет 7, т.е. D=7. Следовательно, в нашем примере величина критерия Колмогорова
По таблицам вероятностей Р (λ) определяем, что λ = 0, 31 соответствует Р(х), близкая к 1, 00. Это означает, что с вероятностью, близкой к 1, можно утверждать, что отклонения фактических частот от теоретических в нашем примере являются случайными. Следовательно, можно считать, что в основе фактического распределения фермерских хозяйств по урожайности лежит нормальное распределение. Этот же вывод подтверждается расчетом χ 2-критерия Пирсона (табл. 7.9). Таблица 7.9 Расчет критерия Пирсона по данным об урожайности зерновых в 500 фермерских хозяйствах
Из данных табл. 7.9 видно, что χ 2 = 5, 05. По таблицам вероятностей Р(χ 2) = 0, 9834. Таким образом, эмпирическое и теоретическое распределения близки. Критерий Романовского Для характеристики структуры вариационных рядов применяются показатели особого рода, которые можно назвать структурными средними.
|
,
.
.
;
.
.
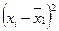
. Для нашего примера эмпирическое корреляционное отношение 
.
.
,
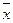– средняя арифметическая ряда распределения,
.
k= 0, 5
.
. Тогда 
. Таким образом, исследуемое распределение является островершинным.
,
– стандартизованная (нормированная) величина;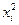
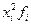
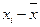
(табл. 7.7 гр. 7) для данного варианта. Значения же теоретической частоты для нее исчисляются по известной уже формуле: 
.
остается одной и той же для всего распределения с равными интервалами, в частности в нашем примере 
, то достаточно ее найти один раз и умножить на величину φ (t) при данном t, тогда получим искомую теоретическую частоту (табл. 7.7 гр. 9).
,
,
,
,
.
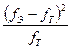
2
1
3
4
. Следовательно, теоретическое распределение эмпирического ряда удовлетворительное.
