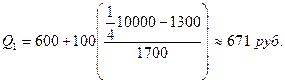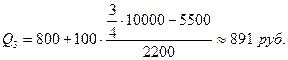Характеристики вариационного ряда
Мода – значение признака, наиболее часто встречающееся в исследуемой совокупности. Медиана – значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности. Для дискретных вариационных рядов модой будет значение варианта с наибольшей частотой. Вычисление медианы в дискретных рядах распределения имеет специфику. Если такой ряд распределения имеет нечетное число членов, то медианой будет вариант, находящийся в середине ранжированного ряда. Если ранжированный ряд распределения состоит из четного числа членов, то медианой будет средняя арифметическая из двух значений признака, расположенных в середине ряда. Пример. Рассчитаем моду и медиану по данным табл. 7.10. Таблица 7.10 Распределение обуви, проданной коммерческой фирмой в январе 1998 г.
В этом ряду распределения мода равна 42. Именно этот размер обуви в январе 1998 г. пользовался наибольшим спросом. Для определения медианы надо подсчитать сумму накопленных частот ряда. Наращивание продолжается до получения накопленной суммы частот, впервые превышающей половину. В нашем примере сумма частот составила 100, ее половина – 50. Накопленная сумма частот ряда равна 62. Ей соответствует значение признака, равное 40. Таким образом, 40-й размер обуви является медианным. Для интервальных вариационных рядов мода определяется по формуле
где хМо – нижняя граница значения интервала, содержащего моду; iМо – величина модального интервала; fMo – частота модального интервала; fMo-1 – частота интервала, предшествующего модальному; fMo+l – частота интервала, следующего за модальным. Медиана интервального ряда распределения определяется по формуле
где хМе – нижняя граница значения интервала, содержащего медиану; iMе – величина медианного интервала; Σ f – сумма частот; SMe-1 – сумма накопленных частот, предшествующих медианному интервалу; fMe – частота медианного интервала Пример. Рассчитаем моду и медиану по данным табл. 7.11.
Следовательно, наибольшее число семей имеют среднедушевой доход 772 руб.
Таким образом, половина семей города имеет среднедушевой доход менее 780 руб., остальные семьи – более 780 руб. Таблица 7.1 Распределение семей города по размеру среднедушевого дохода в январе 1998 г.
Аналогично с нахождением медианы в вариационных рядах можно отыскать значение признака у любой по порядку единицы ранжированного ряда. Например, можно найти значение признака у единиц, делящих ряд на четыре равные части, десять или сто частей. Эти величины называются «квартили», «децили» и «перцентили». Квартили представляют собой значение признака, делящее ранжированную совокупность на четыре равновеликие части. Различают квартиль нижний (Q,), отделяющий 1/4 часть совокупности с наименьшими значениями признака, и квартиль верхний (Q3), отсекающий 1/4 часть с наибольшими значениями признака. Это означает, что 25% единиц совокупности будут меньше по величине Q1; 25% единиц будут заключены между Q1 и Q2; 25% - между Q2 и Q3 и остальные 25% превосходят Q3. Средним квартилем Q2 является медиана. Для расчета квартилей по интервальному вариационному ряду используют формулы:
где
Рассмотрим расчет нижнего и верхнего квартилей по данным табл. 7.11. Нижний квартиль находится в интервале 600-700, накопленная частота которого равна 30%. Верхний квартиль лежит в интервале 800-900 с накопленной частотой 77%. Поэтому получим:
Итак, 25% семей имеют среднедушевой доход менее 671 руб., 25% семей – свыше 891 руб., а остальные имеют доход в пределах 671-891 руб.
|

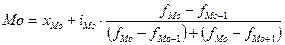 ,
,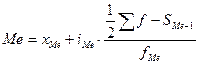 ,
,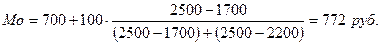
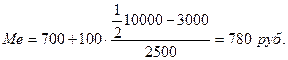
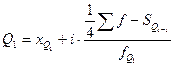 ;
;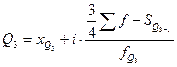 ,
,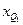 – нижняя граница интервала, содержащего нижний квартиль (интервал определяется по накопленной частоте, первой превышающей 25%);
– нижняя граница интервала, содержащего нижний квартиль (интервал определяется по накопленной частоте, первой превышающей 25%);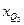 – нижняя граница интервала, содержащего верхний квартиль (интервал определяется по накопленной частоте, первой превышающей 75%);
– нижняя граница интервала, содержащего верхний квартиль (интервал определяется по накопленной частоте, первой превышающей 75%);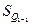 – накопленная частота интервала, предшествующего интервалу, содержащему нижний квартиль;
– накопленная частота интервала, предшествующего интервалу, содержащему нижний квартиль;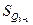 – то же для верхнего квартиля;
– то же для верхнего квартиля;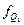 – частота интервала, содержащего нижний квартиль;
– частота интервала, содержащего нижний квартиль;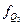 – то же для верхнего квартиля.
– то же для верхнего квартиля.