Методические указания и решение типовых задач
Тема «Выборочное наблюдение» является одной из центральных в курсе теории статистики. Это обусловлено прежде всего взаимосвязью данной темы с другими темами, в особенности, со статистическим наблюдением, статистическими показателями, таблицами, графиками и др. Основываясь на фундаментальных теоретических положениях, в частности, предельных теоремах закона больших чисел (Чебышева-Ляпунова, Бернулли и др.), выборочное наблюдение тесно связано с курсами математической статистики и теории вероятностей. Поэтому освоение теоретического материала, умение правильно решить практические задачи по данной теме, грамотно интерпретировать полученные результаты служат необходимым условием успешного изучения курса теории статистики в целом и связанных с ней наук. Формирование набора задач данной главы обусловлено практическими вопросами, требующими своего решения при организации выборочного наблюдения и анализе его результатов. Такими вопросами являются определение способа отбора и процедуры выборки, вычисление ошибок выборки и построение доверительных интервалов выборочных характеристик, а также расчет необходимого объема выборки. Предложенные в данной теме задания охватывают все эти вопросы с учетом особенностей формирования выборочной совокупности. Расчет ошибок позволяет решить одну из главных проблем организации выборочного наблюдения – оценить репрезентативность (представительность) выборочной совокупности. Различает среднюю и предельную ошибки выборки. Эти два вида ошибок связаны следующим соотношением: Δ = tμ, где Δ – предельная ошибка выборки; μ – средняя ошибка выборки; t – коэффициент доверия, определяемый в зависимости от уровня вероятности (некоторые значения t приведены в приложении). Величина средней ошибки выборки рассчитывается дифференцирование в зависимости от способа отбора и процедуры выборки. Так, при случайном повторном отборе средняя ошибка определяется по формуле
при бесповторном: где σ 2 – выборочная (или генеральная) дисперсия; σ – выборочное (или генеральное) среднее квадратическое отклонение; n – объем выборочной совокупности; N – объем генеральной совокупности. Расчет средней и предельной ошибок выборки позволяет определить возможные пределы, в которых будут находиться характеристики генеральной совокупности. Например, для выборочной средней такие пределы устанавливаются на основе следующих соотношений:
где
Покажем практическое применение рассмотренной выше методики на следующих примерах. Задача 1. При проверке веса импортируемого груза на таможне методом случайной повторной выборки было отобрано 200 изделий. В результате был установлен средний вес изделия 30 г при среднем квадратическом отклонении 4 г. С вероятностью 0, 997 определите пределы, в которых находится средний вес изделий в генеральной совокупности. Решение. Рассчитаем сначала предельную ошибку выборки. Так, при р = 0, 997, t =3
Определим пределы генеральной средней: 30 – 0, 84 ≤ Следовательно, с вероятностью 0, 997 можно утверждать, что средний вес изделий в генеральной совокупности находится в пределах от 29, 16 до 30, 84 г. Задача 2. В городе проживает 250 тыс. семей. Для определения среднего числа детей в семье была организована 2%-ная случайная бесповторная выборка семей. По ее результатам было получено следующее распределение семей по числу детей:
С вероятностью 0, 954 найдите пределы, в которых будет находиться среднее число детей в генеральной совокупности. Решение. Вначале на основе имеющегося распределения семей определим выборочные среднюю и дисперсию:
Вычислим теперь предельную ошибку выборки (с учетом того, что р = 0, 954 t =2).
Следовательно, пределы генеральной средней:
Таким образом, с вероятностью 0, 954 можно утверждать, что среднее число детей в семьях города практически не отличается от 1, 5, т. е. в среднем на каждые две семьи приходятся три ребенка. Наряду с определением ошибок выборки и пределов для генеральной средней эти же показатели могут быть определены для доли признака. В этом случае особенности расчета связаны с определением дисперсии доли, которая вычисляется так:
где Тогда, например, при собственно-случайном повторном отборе для определения предельной ошибки выборки используется следующая формула:
Соответственно при бесповторном отборе
Пределы доли признака в генеральной совокупности р выглядят следующим образом: w – Δ W ≤ p ≤ w +Δ W. Задача 3. С целью определения средней фактической продолжительности рабочего дня в государственном учреждении с численностью служащих 480 человек в июне 1996 г. была проведена 25%-ная механическая выборка. По результатам наблюдения оказалось, что у 10% обследованных потери времени достигали более 45 мин. в день. С вероятностью 0, 683 установите пределы, в которых находится генеральная доля служащих с потерями рабочего времени более 45 мин в день. Решение. Определим объем выборочной совокупности: n = 480 · 0, 25 = 120 человек. Выборочная доля w равна по условию 10%. Учитывая, что показатели точности механической и собственно-случайной бесповторной выборки определяются одинаково, а также то, что при р = 0, 683 t = 1, вычислим предельную ошибку выборочной доли:
Пределы доли признака в генеральной совокупности: 10 – 2, 4 ≤ р ≤ 10 + 2, 4, или 7, 6 ≤ р ≤ 12, 4. Таким образом, с вероятностью 0, 683 можно утверждать, что доля работников учреждения с потерями рабочего времени более 45 мин. в день находится в пределах от 7, 6 до 12, 4 %. Ошибки и пределы генеральных характеристик при других способах формирования выборочной совокупности определяются на основе соответствующих формул, отражающих особенности этих видов выборки. Например, в случае типической выборки показателем вариации является средняя из внутригрупповых дисперсий Следовательно, для типической выборки средняя ошибка вычисляется по формулам: - при отборе, пропорциональном объему типических групп:
- при отборе, пропорциональном вариации признака (не пропорциональных объему групп):
где Ni и ni – объемы i-й типической группы и выборки из нее соответственно;
При серийной выборке средняя ошибка определяется следующим образом:
где R – число серий в генеральной совокупности;
r – число серий в выборочной совокупности. Задача 4. В области, состоящей из 20 районов, проводилось выборочное обследование урожайности на основе отбора серий (районов). Выборочные средние по районам составили соответственно 14, 5 ц/га; 16; 15, 5; 15 и 14 ц/га. С вероятностью 0, 954 найдите пределы урожайности во всей области. Решение. Рассчитаем общую среднюю:
Межгрупповая (межсерийная) дисперсия
Определим теперь предельную ошибку серийной бесповторной выборки (t = 2, р = 0, 954):
Следовательно, урожайность в области с вероятностью 0, 954 будет находиться в пределах: 15 – 1, 7 ≤ Формулы необходимого объема выборки для различных способов формирования выборочной совокупности могут быть выведены из соответствующих соотношений, используемых при расчете предельных ошибок выборки. Приведем наиболее часто применяемые на практике выражения необходимого объема выборки: - собственно-случайная и механическая выборка:
- типическая выборка:
- серийная выборка:
При этом в зависимости от целей исследования дисперсии и ошибки выборки могут быть рассчитаны для средней величины или доли признака. Рассмотрим примеры определения необходимого объема выборки для различных способов формирования выборочной совокупности. Задача 5. В 100 туристических агентствах города предполагается провести обследование среднемесячного количества реализованных путевок методом механического отбора. Какова должна быть численность выборки, чтобы с вероятностью 0, 683 ошибка не превышала 3 путевок, если по данным пробного обследования дисперсия составляет 225? Решение. Рассчитаем необходимый объем выборки:
Задача 6. С целью определения доли сотрудников коммерческих банков области в возрасте старше 40 лет предполагается организовать типическую выборку пропорционально численности сотрудников мужского и женского пола с механическим отбором внутри групп. Общее число сотрудников банков составляет 12 тыс. человек, в том числе 7 тыс. мужчин и 5 тыс. женщин. На основании предыдущих обследований известно, что средняя из внутригрупповых дисперсий составляет 1600. Определите необходимый объем выборки при вероятности 0, 997 и ошибке 5%. Решение. Рассчитаем общую численность типической выборки:
Вычислим объем отдельных типических групп:
Таким образом, необходимый объем выборочной совокупности сотрудников коммерческих банков составляет 550 человек, в том числе 319 мужчин и 231 женщина. Задача 7. В акционерном обществе 200 бригад рабочих. Планируется проведение выборочного обследования с целью определения удельного веса рабочих, имеющих профессиональные заболевания. Известно, что межсерийная дисперсия доли равна 225. С вероятностью 0, 954 рассчитайте необходимое количество бригад для обследования рабочих, если ошибка выборки не должна превышать 5%. Решение. Рассчитаем необходимое количество бригад на основе формулы объема серийной бесповторной выборки: .
|

 ,
, ,
,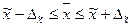 ,
,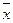 и
и 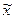 – генеральная и выборочная средние соответственно;
– генеральная и выборочная средние соответственно;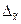 – предельная ошибка выборочной средней.
– предельная ошибка выборочной средней. .
.

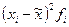
 .
.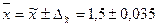 .
. ,
,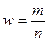 – доля единиц, обладающих данным признаком в выборочной совокупности, определяемая как отношение количества соответствующих единиц к объему выборки.
– доля единиц, обладающих данным признаком в выборочной совокупности, определяемая как отношение количества соответствующих единиц к объему выборки.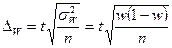 .
.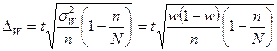
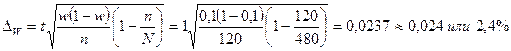 .
.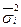 , при серийной выборке – межгрупповая (межсерийная) дисперсия δ 2 и т.д. Кроме того, в последнем случае вместо объема выборочной совокупности n используется показатель числа серий r.
, при серийной выборке – межгрупповая (межсерийная) дисперсия δ 2 и т.д. Кроме того, в последнем случае вместо объема выборочной совокупности n используется показатель числа серий r.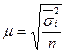 (повторный отбор);
(повторный отбор); (бесповторный отбор);
(бесповторный отбор); (повторный отбор);
(повторный отбор); (бесповторный отбор),
(бесповторный отбор),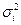 – групповые дисперсии.
– групповые дисперсии. (повторный отбор);
(повторный отбор); (бесповторный отбор),
(бесповторный отбор),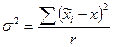 – межгрупповая (межсерийная) дисперсия;
– межгрупповая (межсерийная) дисперсия;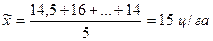 .
.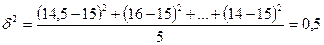
 .
.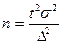 (повторный отбор);
(повторный отбор);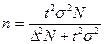 (бесповторный отбор);
(бесповторный отбор); (повторный отбор);
(повторный отбор);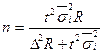 (бесповторный отбор);
(бесповторный отбор);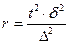 (повторный отбор);
(повторный отбор);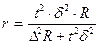 (бесповторный отбор).
(бесповторный отбор).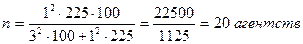 .
.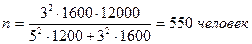
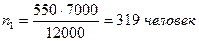 ;
;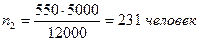 .
.


