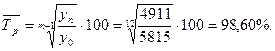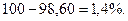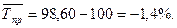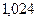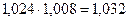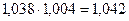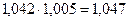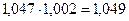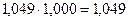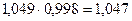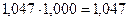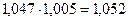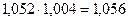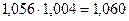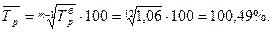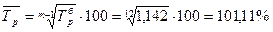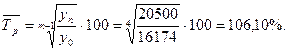Показатели анализа ряда динамики
Тема 8. Статистическое изучение динамики
Цель занятия: освоить методику исчисления показателей ряда динамики, средних показателей в рядах динамики.
Методические указания. Задача 1. Имеются данные о числе родившихся в Чувашской Республике за 2005-2010 гг., чел. (табл. 135). Таблица 135 – Число родившихся
Определите аналитические показатели ряда динамики числа родившихся в Чувашской Республике за 2005 – 2010 гг.: 1) абсолютные приросты; 2) темпы роста; 3) темпы прироста; 4) абсолютное значение одного процента прироста, а также средние показатели (средний уровень ряда и средние показатели изменения уровней ряда). Сделайте прогноз на три предстоящих года по среднему абсолютному приросту и среднему темпу роста. Постройте график. Решение. В зависимости от задачи исследования абсолютные приросты 1. Абсолютный прирост Абсолютный прирост базисный рассчитывается по формуле:
Так, Абсолютный прирост цепной рассчитывается по формуле:
Так, Таблица 136 - Динамика числа родившихся в Чувашской Республике
Следует отметить, что сумма цепных абсолютных приростов равна последнему базисному абсолютному приросту. 2. Темп роста Темп роста базисный определяется отношением каждого последующего уровня к базисному значению по формуле:
Так, Темп роста цепной определяется отношением последующего уровня к предыдущему по формуле:
Так, Между цепными и базисными темпами роста имеется взаимосвязь: произведение соответствующих цепных темпов роста равно базисному. Зная базисные темпы, можно исчислить цепные делением каждого последующего базисного темпа роста на каждый предыдущий. 3. Темп прироста а) темп прироста базисный - отношение абсолютного прироста базисного к базисному значению:
Так, Темп прироста цепной - отношение абсолютного прироста цепного к цепному значению:
Так, б) как разность между коэффициентом роста и единицей, если темпы роста выражены в коэффициентах:
или как разность между темпами роста и 100 %, еслитемпы роста выражены в процентах:
Так,
4. Абсолютное значение одного процента прироста а) отношение абсолютного прироста цепного к темпу прироста цепного:
Так, б) как одна сотая часть предыдущего уровня:
Так, Средний уровень ряда рассчитаем по формуле:
Средний абсолютный прирост исчисляется двумя способами: а) как средняя арифметическая простая годовых абсолютных (цепных) приростов
б) как отношение базисного абсолютного прироста к числу периодов
Средний темп роста исчисляется двумя способами: а) как средняя геометрическая цепных коэффициентов роста по «цепному» способу
б) по «базисному» способу
Средний темп прироста определим по формуле:
или средний коэффициент роста:
Так, Таким образом, ежегодно в Чувашской Республике увеличилось число родившихся на 608 человек, или на 4, 25 %. Составим прогноз числа родившихся в Чувашской Республике на предстоящие три года по среднему абсолютному приросту по формуле:
По среднему темпу роста прогнозные показатели определим по формуле:
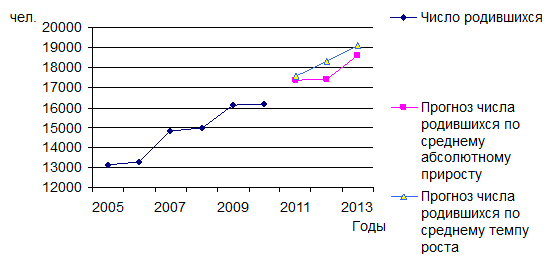
Более наглядно этот прогноз изобразим на графике (рис. 10).
Рис. 10. Динамика и прогноз числа родившихся в Чувашской Республике Таким образом, по нашим прогнозам в Чувашии будет отмечаться рост рождаемости.
Задача 2. Привести ряды динамики к общему (единому) основанию и рассчитать коэффициенты опережения (отставания) (табл. 137). Таблица 137 – Динамика численности населения (чел.) и базисные темпы изменения численности населения
Решение. Рассчитаем базисные темпы роста (снижения) численности населения в обоих республиках и занесем данные в таблицу 138. Таблица 138 – Темпы роста (снижения) базисные численности населения
Сравним интенсивность изменения уровней ряда во времени с помощью коэффициентов опережения (отставания), представляющих собой отношение базисных темпов роста (или прироста) двух рядов динамики за одинаковые отрезки времени:
где Так,
где Рассчитать коэффициент опережения (отставания) можно на основе сравнения средних темпов роста (или прироста) двух динамических рядов за одинаковый период времени:
где
Задача 3. Имеются данные о динамике общей численности безработных на 01.2011 г. по 01.2012 г. в Российской Федерации, тыс. чел. (табл. 139). Определите аналитические показатели ряда динамики численности безработных в Российской Федерации: 1) абсолютные приросты; 2) темпы роста; 3) темпы прироста; 4) абсолютное значение одного процента прироста, а также средние показатели (средний уровень ряда и средние показатели изменения уровней ряда). Решение. Таблица 139 – Динамика общей численности безработных в Российской Федерации, тыс. чел.
Продолжение таблицы 139
Средний уровень ряда рассчитаем по формуле средней хронологической:
Средний абсолютный прирост (снижение) исчислим как отношение базисного абсолютного прироста к числу периодов:
Таким образом, ежемесячно число безработных сокращалось в среднем на 75 чел. Средний темп роста исчислим по «базисному» способу:
Таким образом, ежемесячно число безработных сокращалось на Средний темп прироста определим по формуле: Так,
Задача 4. Индексы потребительских цен на товары и услуги в Российской Федерации за 2011 г. характеризуются следующими темпами роста к предыдущему месяцу (табл. 140). Таблица 140 - Индексы потребительских цен на товары и услуги в Российской Федерации за 2011 г.
Определите базисные темпы роста потребительских цен на товары и услуги в декабре 2011 г. к декабрю 2010 г.; среднемесячный темп прироста потребительских цен на товары и услуги с января по декабрь 2011 г. Решение. Рассчитаем базисные темпы роста в табл. 141. Таблица 141 – Темпы роста индексов потребительских цен на товары и услуги в Российской Федерации за 2011 г.
Базисный темп роста индексов потребительских цен на товары и услуги в январе 2011 г. к декабрю 2010 г. равен 106, 0 %, т.е. темп прироста равен 6, 0 %. Среднемесячный темп роста индексов потребительских цен на товары и услуги с января по декабрь 2011 г. рассчитаем по формуле:
Следовательно, среднемесячный темп прироста индексов потребительских цен на товары и услуги с января по декабрь 2011 г. составил 0, 49 %.
Задача 5. Индексы потребительских цен в группировке классификатора индивидуального потребления по целям (КИПЦ) на конец периода, в % к декабрю предыдущего года представлен в таблице 142. Таблица 142 - Индексы потребительских цен в группировке классификатора индивидуального потребления по целям (КИПЦ)
Продолжение таблицы 142
Определите среднемесячный темп роста индекса потребительских цен с января по декабрь соответствующего года по каждому наименованию групп и видов товаров. Решение. Среднемесячный темп роста индексов потребительских цен на продукты питания и безалкогольные напитки с января по декабрь 2010 г. рассчитаем по формуле:
и т.д. (далее рассчитайте самостоятельно).
Задача 6. Определите какими темпами должно расти число родившихся в Чувашской Республике, чтобы с 16174 чел. в 2014 г. оно возросло до 20500 чел. в 2013 г? Решение. Таким образом, среднегодовой темп прироста число родившихся в Чувашской Республике должен быть 6, 10 %.
Задачи для самостоятельной работы: Задача 1. Имеются данные о числе родившихся г. Чебоксары за 2005-2010 гг., чел. (табл. 143). Таблица 143 – Число родившихся
Определите аналитические показатели ряда динамики числа родившихся в г. Чебоксары за 2005 – 2010 гг.: 1) абсолютные приросты; 2) темпы роста; 3) темпы прироста; 4) абсолютное значение одного процента прироста, а также средние показатели (средний уровень ряда и средние показатели изменения уровней ряда). Сделайте прогноз на три предстоящих года по среднему абсолютному приросту и среднему темпу роста. Постройте график.
Задача 2. Имеются данные о числе родившихся в г. Алатырь за 2005-2010 гг., чел. (табл. 144). Таблица 144 – Число родившихся
Определите аналитические показатели ряда динамики числа родившихся в г. Алатырь за 2005 – 2010 гг.: 1) абсолютные приросты; 2) темпы роста; 3) темпы прироста; 4) абсолютное значение одного процента прироста, а также средние показатели (средний уровень ряда и средние показатели изменения уровней ряда). Сделайте прогноз на три предстоящих года по среднему абсолютному приросту и среднему темпу роста. Постройте график.
Задача 3. Имеются данные о числе родившихся в г. Канаш за 2005-2010 гг., чел. (табл. 145). Таблица 145 – Число родившихся
Определите аналитические показатели ряда динамики числа родившихся в г. Канаш за 2005 – 2010 гг.: 1) абсолютные приросты; 2) темпы роста; 3) темпы прироста; 4) абсолютное значение одного процента прироста, а также средние показатели (средний уровень ряда и средние показатели изменения уровней ряда). Сделайте прогноз на три предстоящих года по среднему абсолютному приросту и среднему темпу роста. Постройте график.
Задача 4. Имеются данные о числе родившихся в Новочебоксарск за 2005-2010 гг., чел. (табл. 146). Таблица 146 – Число родившихся
Определите аналитические показатели ряда динамики числа родившихся в г. Новочебоксарск за 2005 – 2010 гг.: 1) абсолютные приросты; 2) темпы роста; 3) темпы прироста; 4) абсолютное значение одного процента прироста, а также средние показатели (средний уровень ряда и средние показатели изменения уровней ряда).
Задача 5. Имеются данные о числе родившихся в г. Шумерля за 2005-2010 гг., чел. (табл. 147). Таблица 147 – Число родившихся
Определите аналитические показатели ряда динамики числа родившихся в г. Шумерля за 2005 – 2010 гг.: 1) абсолютные приросты; 2) темпы роста; 3) темпы прироста; 4) абсолютное значение одного процента прироста, а также средние показатели (средний уровень ряда и средние показатели изменения уровней ряда). Сделайте прогноз на три предстоящих года по среднему абсолютному приросту и среднему темпу роста. Постройте график.
Задача 6. Имеются данные о среднемесячной номинальной начисленной заработной плате работников организаций Чувашской Республики за 2005-2010 гг., руб. (табл. 148). Таблица 148 – Среднемесячная номинальная начисленная заработная плата работников организаций
Определите аналитические показатели ряда динамики среднемесячной номинальной начисленной заработной платы работников организаций Чувашской Республики за 2005 – 2010 гг.: 1) абсолютные приросты; 2) темпы роста; 3) темпы прироста; 4) абсолютное значение одного процента прироста, а также средние показатели (средний уровень ряда и средние показатели изменения уровней ряда). Сделайте прогноз на три предстоящих года по среднему абсолютному приросту и среднему темпу роста. Постройте график.
Задача 7. Имеются данные о численности детей в дошкольных образовательных учреждениях Чувашской Республики на конец года за 2005-2010 гг. (табл. 149). Таблица 149 – Численность детей в дошкольных образовательных учреждениях Чувашской Республики, чел.
Определите аналитические показатели ряда динамики численности детей в дошкольных образовательных учреждениях Чувашской Республики за 2005 – 2010 гг.: 1) абсолютные приросты; 2) темпы роста; 3) темпы прироста; 4) абсолютное значение одного процента прироста, а также средние показатели (средний уровень ряда и средние показатели изменения уровней ряда). Сделайте прогноз на три предстоящих года по среднему абсолютному приросту и среднему темпу роста. Постройте график.
Задача 8. Имеются данные о числе предприятий и организаций Чувашской Республики за 2006-2011 гг., чел. (табл. 150). Таблица 150 – Число предприятий и организаций Чувашской Республики
Определите аналитические показатели ряда динамики числа предприятий и организаций Чувашской Республики за 2005 – 2010 гг.: 1) абсолютные приросты; 2) темпы роста; 3) темпы прироста; 4) абсолютное значение одного процента прироста, а также средние показатели (средний уровень ряда и средние показатели изменения уровней ряда). Сделайте прогноз на три предстоящих года по среднему абсолютному приросту и среднему темпу роста. Постройте график.
Задача 9. Имеются данные о продукции сельского хозяйства в хозяйствах всех категорий в фактически действовавших ценах за 2005-2010 гг., млн. руб. (табл. 151). Таблица 151 – Продукция сельского хозяйства в хозяйствах всех категорий
Определите аналитические показатели ряда динамики продукции сельского хозяйства в хозяйствах всех категорий Чувашской Республики за 2005 – 2010 гг.: 1) абсолютные приросты; 2) темпы роста; 3) темпы прироста; 4) абсолютное значение одного процента прироста, а также средние показатели (средний уровень ряда и средние показатели изменения уровней ряда). Сделайте прогноз на три предстоящих года по среднему абсолютному приросту и среднему темпу роста. Постройте график.
Задача 10. Имеются данные о посевных площадях сельскохозяйственных культур в хозяйствах всех категорий Чувашской Республики за 2005-2010 гг., чел. (табл. 152). Таблица 152 – Посевные площади сельскохозяйственных культур в хозяйствах всех категорий Чувашской Республики
Определите аналитические показатели ряда динамики посевных площадей сельскохозяйственных культур в хозяйствах всех категорий Чувашской Республики за 2005 – 2010 гг.: 1) абсолютные приросты; 2) темпы роста; 3) темпы прироста; 4) абсолютное значение одного процента прироста, а также средние показатели (средний уровень ряда и средние показатели изменения уровней ряда). Сделайте прогноз на три предстоящих года по среднему абсолютному приросту и среднему темпу роста. Постройте график.
Задача 11. Имеются данные о посевных площадях овощей открытого грунта (без высадков) в хозяйствах всех категорий Чувашской Республики за 2005-2010 гг., чел. (табл. 153). Таблица 153 – Посевные площади овощей открытого грунта (без высадков) в хозяйствах всех категорий Чувашской Республики
Определите аналитические показатели ряда динамики посевных площадей овощей открытого грунта (без высадков) в хозяйствах всех категорий Чувашской Республики за 2005 – 2010 гг.: 1) абсолютные приросты; 2) темпы роста; 3) темпы прироста; 4) абсолютное значение одного процента прироста, а также средние показатели (средний уровень ряда и средние показатели изменения уровней ряда). Сделайте прогноз на три предстоящих года по среднему абсолютному приросту и среднему темпу роста. Постройте график.
Задача 12. Имеются данные о внесении минеральных удобрений в пересчете на 100% питательных веществ под посев сельскохозяйственных культур в Чувашской Республике (табл. 154). Таблица 154 – Внесение минеральных удобрений в пересчете на 100% питательных веществ, тонн
Определите аналитические показатели ряда динамики внесения минеральных удобрений под посев сельскохозяйственных культур в Чувашской Республике за 2005 – 2010 гг.: 1) абсолютные приросты; 2) темпы роста; 3) темпы прироста; 4) абсолютное значение одного процента прироста, а также средние показатели (средний уровень ряда и средние показатели изменения уровней ряда). Сделайте прогноз на три предстоящих года по среднему абсолютному приросту и среднему темпу роста. Постройте график.
Задача 13. Имеются данные о производстве яиц в хозяйствах всех категорий в Приволжском федеральном округе за 2005-2010 гг., млн. шт. (табл. 155). Таблица 155 – Производство яиц
Определите аналитические показатели ряда динамики производства яиц: 1) абсолютные приросты; 2) темпы роста; 3) темпы прироста; 4) абсолютное значение одного процента прироста, а также средние показатели (средний уровень ряда и средние показатели изменения уровней ряда). Сделайте прогноз на три предстоящих года по среднему абсолютному приросту и среднему темпу роста. Постройте график.
Задача 14. Имеются данные о производстве яиц в хозяйствах всех категорий Чувашской Республики за 2005-2010 гг., млн. шт. (табл. 156). Таблица 156 – Производство яиц
Определите аналитические показатели ряда динамики производства яиц: 1) абсолютные приросты; 2) темпы роста; 3) темпы прироста; 4) абсолютное значение одного процента прироста, а также средние показатели (средний уровень ряда и средние показатели изменения уровней ряда). Сделайте прогноз на три предстоящих года по среднему абсолютному приросту и среднему темпу роста. Постройте график.
Задача 15. Имеются данные о производстве шерсти в хозяйствах всех категорий в физическом весе в Чувашской Республике за 2005-2010 гг., тонн (табл. 157). Таблица 157 – Производство шерсти
Определите аналитические показатели ряда динамики производства шерсти: 1) абсолютные приросты; 2) темпы роста; 3) темпы прироста; 4) абсолютное значение одного процента прироста, а также средние показатели (средний уровень ряда и средние показатели изменения уровней ряда). Сделайте прогноз на три предстоящих года по среднему абсолютному приросту и среднему темпу роста. Постройте график.
Задача 16. Имеются данные о производстве меда в хозяйствах всех категорий в Чувашской республике за 2005-2010 гг., тонн (табл. 158). Таблица 158 – Производство меда
Определите аналитические показатели ряда динамики производства меда: 1) абсолютные приросты; 2) темпы роста; 3) темпы прироста; 4) абсолютное значение одного процента прироста, а также средние показатели (средний уровень ряда и средние показатели изменения уровней ряда). Сделайте прогноз на три предстоящих года по среднему абсолютному приросту и среднему темпу роста. Постройте график.
Задача 17. Имеются данные о надое молока от одной коровы в сельскохозяйственных организациях Чувашской Республики за 2005-2010 гг., кг (табл. 159). Таблица 159 – Динамика надоя молока на одну корову
Определите аналитические показатели ряда динамики производства молока от одной коровы: 1) абсолютные приросты; 2) темпы роста; 3) темпы прироста; 4) абсолютное значение одного процента прироста, а также средние показатели (средний уровень ряда и средние показатели изменения уровней ряда). Сделайте прогноз на три предстоящих года по среднему абсолютному приросту и среднему темпу роста. Постройте график.
Задача 18. Имеются данные о среднегодовой яйценоскости кур-несушек в сельскохозяйственных организациях Чувашской Республики за 2005-2010 гг., шт. (табл. 160). Таблица 160 – Среднегодовая яйценоскость кур-несушек
Определите аналитические показатели ряда динамики среднегодовой яйценоскости кур-несушек: 1) абсолютные приросты; 2) темпы роста; 3) темпы прироста; 4) абсолютное значение одного процента прироста, а также средние показатели (средний уровень ряда и средние показатели изменения уровней ряда). Сделайте прогноз на три предстоящих года по среднему абсолютному приросту и среднему темпу роста. Постройте график.
Задача 19. Имеются данные о численности официально зарегистрированных безработных на 01.2011 г. по 01.2012 г. в Российской Федерации, чел. (табл. 161).
Таблица 161 – Динамика численности официально зарегистрированных безработных в Российской Федерации, тыс. чел.
Определите аналитические показатели ряда динамики численности безработных за 2005 – 2010 гг.: 1) абсолютные приросты; 2) темпы роста; 3) темпы прироста; 4) абсолютное значение одного процента прироста, а также средние показатели (средний уровень ряда и средние показатели изменения уровней ряда). Сделайте прогноз на три предстоящих месяца по среднему абсолютному приросту и среднему темпу роста. Постройте график. Задача 20. Индексы потребительских цен на продовольственные товары по Российской Федерации за 2010 г. характеризуются следующими темпами роста к предыдущему месяцу (табл. 162). Таблица 162 - Индексы потребительских цен на продовольственные товары по Российской Федерации за 2010 г.
Определите базисные темпы роста потребительских цен на продовольственные товары по Российской Федерации в декабре 2010 г. к декабрю 2009 г.; среднемесячный темп прироста потребительских цен на продовольственные товары с января по декабрь 2010 г.
Задача 21. Индексы потребительских цен на продовольственные товары по Российской Федерации за 2011 г. характеризуются следующими темпами роста к предыдущему месяцу (табл. 163). Таблица 163 - Индексы потребительских цен на продовольственные товары по Российской Федерации за 2011 г.
Определите базисные темпы роста потребительских цен на продовольственные товары по Российской Федерации в декабре 2011 г. к декабрю 2010 г.; среднемесячный темп прироста потребительских цен на продовольственные товары с января по декабрь 2011 г.
Задача 22. Индексы потребительских цен на непродовольственные товары
|

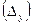 , темпы роста
, темпы роста 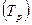 и темпы прироста
и темпы прироста 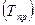 могут быть исчислены с использованием постоянной базы сравнения (базисные) и переменной базы сравнения (цепные).
могут быть исчислены с использованием постоянной базы сравнения (базисные) и переменной базы сравнения (цепные).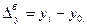 (35)
(35)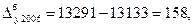
 и т.д.
и т.д.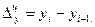 (36)
(36)
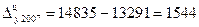 и т.д.
и т.д.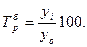 (37)
(37)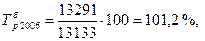
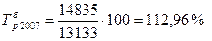 и т.д.
и т.д.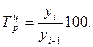 (38)
(38)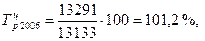
 и т.д.
и т.д.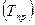 определяют двумя способами:
определяют двумя способами: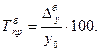 (39)
(39)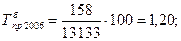
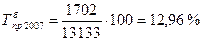 и т.д.
и т.д. (40)
(40)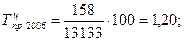
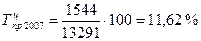 и т.д.
и т.д.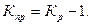 (41)
(41)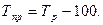 (42)
(42)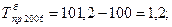
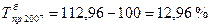 и т.д.
и т.д.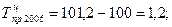
 и т.д.
и т.д. так же исчисляют двумя путями:
так же исчисляют двумя путями: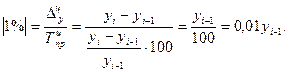 (43)
(43)
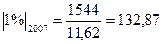 и т.д.
и т.д.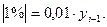 (44)
(44)
 и т.д.
и т.д.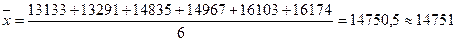 чел.
чел.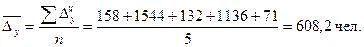

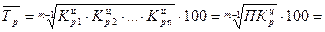
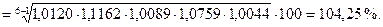
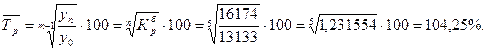
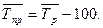 (45)
(45) (46)
(46)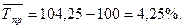
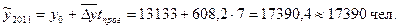
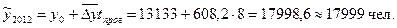
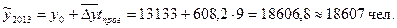
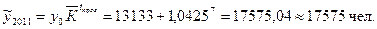
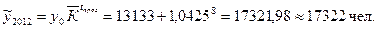
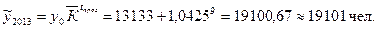
 (47)
(47)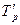 ,
, 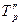 - базисные темпы роста первого и второго рядов динамики.
- базисные темпы роста первого и второго рядов динамики.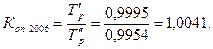 Таким образом, численность населения в 2006 г. в Чувашской Республике сократилась в 1, 0041 раза больше по сравнению с Татарстаном и т.д.
Таким образом, численность населения в 2006 г. в Чувашской Республике сократилась в 1, 0041 раза больше по сравнению с Татарстаном и т.д.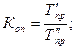 (48)
(48)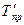 ,
, 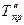 - базисные темпы прироста первого и второго рядов динамики.
- базисные темпы прироста первого и второго рядов динамики.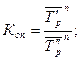 (49)
(49) ,
, 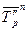 - средние темпы роста первого и второго рядов динамики.
- средние темпы роста первого и второго рядов динамики.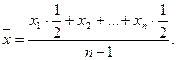 (50)
(50)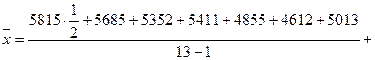
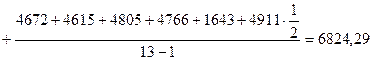 чел.
чел.