Теплообмен излучением между телами

 

Эффективным (фактическим) излучением тела называется сумма собственного и отраженного излучений

 

Е_эф = Е_соб + Е_отр = Е_соб + R · E_пад.= Е_соб +(1 – А – D) · E_пад.

 

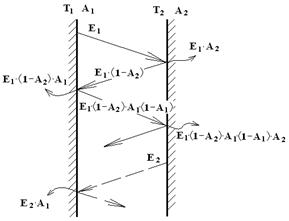
Рассмотрим случай теплообмена излучением между двумя параллельными непрозрачными поверхностями бесконечной длины, между которыми находится абсолютно прозрачная (диатермичная) среда (D=0)
(рис. 13).

 

Рис. 13. Теплообмен излучением между двумя параллельными поверхностями

 

Количество теплоты, которое передается от поверхности 1 к поверхности 2

q_1-2 = E_1эф – E_2эф. (6.3)

 

Эффективное излучение поверхности 1 складывается из собственного излучения и отраженного излучения, посланного 2 поверхности. Аналогично записывается эффективное излучение поверхности 2

 

E_1эф = Е₁ + (1 – A₁) · E_2эф , (6.4)

 

E_2эф = Е₂ + (1 – A₂) · E_1эф . (6.5)

 

Решая совместно уравнения (6.4) и (6.5) и подставляя полученное решение в уравнение (6.3), получаем

 

q_1-2 = (А₂ · Е₁ – А₁ · Е₂) / (А₁ + А₂ - А₁ · А₂).(6.6)

 

В соответствии с формулой закона Стефана-Больцмана (5.1)

Е₁ = ε ₁ · С₀ · (T₁ /100)⁴, (6.7)

 

Е₂ = ε ₂ · С₀ · (T₂ /100)⁴.(6.8)

В соответствии с законом Кирхгофа

ε ₁ = А_1, (6.9)

 

ε ₂ = А_2. (6.10)

После подстановки (6.7), (6.8) в (6.6) с учетом (6.9) - (6.10), можем записать

 

q_1-2 = ε _пр ·С₀ ·[ (T₁ /100)⁴ – (T₂ /100)⁴],

 

где

ε _пр = 1 / (1/ ε ₁ + 1/ ε ₂ – 1).

 

Аналогично может быть получено выражение для теплообмена излучением, когда поверхности находятся одна внутри другой (рис. 14).

Приведенный коэффициент излучения в этом случае имеет вид

 

ε _пр = 1 / [ 1/ ε ₁ + (1/ ε ₂ – 1) · F₁/F₂].

Из последнего выражения видно, что если F₁ < < F₂ , то ε _пр ≈ ε ₁ .

 

Рис. 14. Теплообмен излучением, когда поверхности находятся одна внутри другой