Уравнение теплопередачи

 

Наряду с уравнением теплового баланса, при расчете теплообменных аппаратов широко применяется уравнение теплопередачи

 

Q = k ∙ F ∙ Δ t_ср.лог, (7.2)

 

где k – коэффициент теплопередачи, Вт/(м²∙ К), F – площадь поверхности теплообменника, м², Δ t_ср.лог – средний логарифмический температурный напор, º С.

Средний логарифмический температурный напор определяется по формуле

Δ t_ср.лог = (Δ t_max - Δ t_min) / ℓ n (Δ t_max/Δ t_min), (7.3)

 

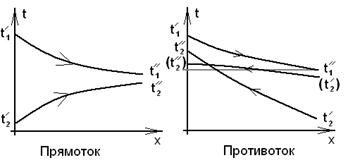
где Δ t_max и Δ t_min – наибольшая и наименьшая разности температур теплоносителей на входе и на выходе из теплообменника, º С.

Для прямотока наибольшая разность температур всегда равна

Δ t_max = t₁^' – t₂'

 

и наблюдается на входе в теплообменник. Наименьшая разность температур при прямотоке наблюдается на выходе из теплообменника
(рис. 20) и соответственно равна

 

Δ t_min = t₁^" – t₂".

 

При противотоке наибольшая и наименьшая разности температур могут наблюдаться как на входе, так и на выходе из теплообменника и соответственно равны

Δ t_max = t₁" – t₂^',

Δ t_min = t₁^' – t₂"

 

или

Δ t_max = t₁^' – t₂",

Δ t_min = t₁" – t₂^'.

 

Коэффициент теплопередачи, который характеризует интенсивность теплопередачи от более нагретого теплоносителя к менее нагретому через разделяющую их стенку, в случае однослойной плоской стенки вычисляется по соотношению

 

k = 1 / (1/α ₁ + δ /λ + 1/α ₂), (7.4)

где α _1, α ₂ – коэффициенты теплоотдачи от горячего теплоносителя к стенке и от стенки к нагреваемому теплоносителю, соответственно, Вт/(м²∙ К), δ и λ – толщина стенки и ее коэффициент теплопроводности, соответственно, м и Вт/(м∙ К).

 

Рис. 20. Изменение температур теплоносителей

при прямотоке и противотоке

 

Применительно к цилиндрической стенке линейный коэффициент теплопередачи (при отнесении теплового потока к единице длины цилиндрической стенки) имеет вид

 

k_ℓ = 1 / [1/α ₁ + d₁/(2∙ λ)∙ ℓ n(d₂/d₁) + d₁/(α ₂∙ d₂)], (7.5)

 

где d₁ и d₂ внутренний и наружный диаметры цилиндрической стенки, соответственно. Поверхностный коэффициент теплопередачи, когда тепловой поток относится к единице наружной поверхности цилиндрической стенки

 

k_f = 1 / [d₂/(α ₁∙ d₁) + d₂/(2∙ λ)∙ ℓ n(d₂/d₁) + 1/α ₂]. (7.6)

 

Входящие в формулы (7.4) – (7.6) коэффициенты теплоотдачи α ₁ и α ₂ определяются из уравнений подобия. Числовые значения коэффициентов теплоотдачи зависят от режима течения жидкости и формы поперечного сечения канала.

В случае ламинарного [5] течения жидкости в трубах круглого поперечного сечения на начальном участке гидродинамической и тепловой стабилизации, если q_c = const, уравнение подобия имеет вид
[4, с. 215]

 

Nu = 4, 36·[1+0, 032·(d₁/x)·Re·Pr^5/6]^{0, 4}·(Pr_ж/Pr_с)^{0, 25}, (7.7)

 

где d₁ – внутренний диаметр трубы, м; x – расстояние от входа в трубу, м. В качестве определяющей температуры берется температура жидкости в рассматриваемом сечении трубы, определяющим размером является внутренний диаметр трубы d₁, м. Уравнение (7.7) позволяет рассчитать местные значения коэффициентов теплоотдачи.

В случае ламинарного течения жидкости в трубах круглого поперечного сечения на участке установившегося течения и теплообмена, если q_c = const, уравнение подобия имеет вид [4, с.215]

 

Nu_∞ = 4, 36. (7.8)

 

В этом уравнении используются те же определяющие параметры, что и в уравнении (7.7). Уравнение (7.8) позволяет рассчитать местные значения коэффициентов теплоотдачи.

При ламинарном течении жидкости в кольцевых каналах при теплоотдаче на внутренней стенке (1) трубы при теплоизолированной внешней (2) уравнение подобия записывается в виде [4, с.216]

 

Nu_{∞ 1} = 4, 2 + 1, 18 ∙ (d₂/d₁)^{0, 81}, (7.9)

 

где d₁ и d₂ – внутренний и наружный диаметры кольцевого канала, соответственно. В качестве определяющей температуры берется температура жидкости в рассматриваемом сечении трубы, определяющим размером – эквивалентный диметр d_э = d₂ – d₁, м. Уравнение (7.9) позволяет рассчитать местные значения коэффициентов теплоотдачи.

При турбулентном течении жидкости в трубах круглого поперечного сечения [6] уравнение подобия имеет вид [4, с.216]

 

Nu_∞ = (ζ / 8) ∙ Re ∙ Pr / [ 1+(900/Re) + 12, 7 ∙ (ζ / 8)^1/2 ∙ (Pr^2/3 –1)], (7.10)

 

где коэффициент гидравлического сопротивления ζ = (1, 82 ∙ ℓ g Re –1, 64)^-2, Re = Ŵ ∙ d₁ / ν, Nu_∞ = α _∞ ∙ d₁ / λ. В качестве определяющей температуры берется температура жидкости в рассматриваемом сечении трубы, определяющим размером является внутренний диметр трубы d₁, м. Уравнение (7.9) позволяет рассчитать местные значения коэффициентов теплоотдачи. Если окажется, что длина трубы, отнесенная к диаметру ℓ / d₁ > 60, то по этому уравнению можно определить и среднюю теплоотдачу жидкости в трубе. В этом случае в качестве определяющей температуры берется средняя температура жидкости в трубе. Уравнение (7.10) справедливо при Re = 4∙ 10³ … 5∙ 10⁶ и Pr = 0, 5 … 5∙ 10³.

При переходном режиме течения жидкости в трубах круглого поперечного сечения[7] при расчетах пользуются формулой [4, с.220]

 

Nu_∞ = (ζ / 8) ∙ Pr ∙ (Re – 1000) / [ 1 + 12, 7 ∙ (ζ / 8)^1/2 ∙ (Pr^2/3 –1)]. (7.11)

 

В этом уравнении используются те же определяющие параметры, что и в уравнении (7.10). Уравнение справедливо при Re = 2300 … 4∙ 10³ и Pr = 0, 5 … 200.

Для турбулентного режима течения жидкости в кольцевых каналах при теплоотдаче на внутренней стенке (10) трубы при необогреваемой внешней (20) уравнение подобия записывается в виде [4, с.220]

 

Nu₁₀=(ζ / 8)∙ [0, 96+0, 04∙ (d₂/d₁)]∙ Re∙ Pr/[C+(11, 7+1, 8∙ Pr ^–1/3)

(ζ / 8)^1/2∙ (Pr^2/3-1)], (7.12)

 

где C = (1+3, 4∙ ζ)∙ [1+(d₁/d₂)/(1, 15+5, 5∙ (d₁/d₂))], ζ = [1, 82∙ ℓ g Re –1, 64-0, 19∙ (d₁/d₂)^{0, 25}]^-2, Re = Ŵ ∙ d_э / ν, Nu₁₀ = α ∙ d_э / λ, d₁ и d₂ внутренний и наружный диаметры кольцевого канала, соответственно. В качестве определяющей температуры берется температура жидкости в рассматриваемом сечении трубы, определяющим размером является эквивалентный диметр d_э = d₂ – d₁, м. Уравнение (7.12) позволяет рассчитать местные значения коэффициентов теплоотдачи.