ТЕМА № 2. ЛОГИКА ВЫСКАЗЫВАНИЙ
Высказывание. Простые и составные высказывания. Операции над высказываниями: отрицание, конъюнкция, дизъюнкция, импликация, эквиваленция. Таблицы истинности. Способы построения отрицания высказываний. Литература: [1] с. 5-23; [2] с. 29-38; [3] с. 5-15; [4] с. 5-11; [5] с. 33-46; [6] с. 37-42; [7] с. 57-71.
ЛОГИКА ВЫСКАЗЫВАНИЙ (задания 1 уровня)
1А. Какие из следующих предложений являются высказываниями? Для высказываний определите их значения истинности: а) число 25 делится на 5; б) 23+7; в) 3> 7; г) Минск – столица Беларуси; д) все числа делятся на 8.
1Б. Постройте отрицание высказывания Р и определите его значение истинности: а) Р: «Число 105 делится на 3»; б) Р: «Число 23 не делится без остатка на 3»; в) Р: «В прямоугольнике все углы прямые»; г) Р: «Квадрат является ромбом».
2А. Какие из следующих предложений определяют высказывания? Определите их значения истинности: а) существуют хÎ R, что х+2< 5; б) сегодня хорошая погода; в) ты любишь математику?; г) существуют простые числа.
2Б. Сформулируйте отрицания высказываний, встречающихся в начальной школе: а) Алеша моложе Тани; б) масса кролика меньше массы гуся; в) тетрадь дороже карандаша; г) красный отрезок длинней синего.
3А. Среди данных предложений укажите высказывания. Определите их значения истинности: а) число 2 – простое; б) слово «делится» является глаголом; в) в каком году родился А.С. Пушкин? г) лось является парнокопытным животным.
3Б. Найдите значения истинности высказываний А и В и объясните, почему они не являются отрицаниями друг друга: а) А: «Слово «сад» – прилагательное», В: «Слово «сад» – наречие»; б) А: «Все треугольники являются равнобедренными», В: «Все треугольники не являются равнобедренными»; в) А: «Некоторые слова могут быть разделены на слоги», В: «Некоторые слова не могут быть разделены на слоги».
4А. Какие из следующих предложений являются высказываниями? Для высказываний определите их значения истинности: а) на 0 делить нельзя; б) пусть всегда будет солнце! в) 11–2=9; г) существуют хÎ R, что х+3≥ 52.
4Б. Выясните какие из высказываний каждой пары являются отрицаниями друг друга: а) А: «В книге 100 страниц», В: «В книге не более 100 страниц»; б) А: «Эта гвоздика красная», В: «Эта гвоздика розовая»; в) А: «Эта гвоздика красная», В: «Эта гвоздика не красная»; г) А: «Данное слово − существительное», В: «Данное слово − прилагательное».
5А. Среди данных предложений укажите высказывания. Определите их значения истинности: а) число а делится на 5; б) существуют четные простые числа; в) берегите мир! г) некоторые высказывания не являются истинными.
5Б. Найдите значения истинности высказываний М и К и объясните, почему они не являются отрицаниями друг друга: а) М: «Все студенты – отличники», N: «Все студенты – не отличники»; б) М: «Некоторые числа записываются с помощью цифр», N: «Некоторые числа не записываются с помощью цифр»; в) М: «25 – отрицательное число», N: «25 – четное число».
0А. Среди данных предложений укажите высказывания. Определите их значения истинности: а) брусника – растение, характерное для хвойного леса; Решение: Это высказывание. Оно истинно, т.к. брусника является растением, характерным для хвойного леса. б) некоторые высказывания являются ложными; Решение: Это высказывание истинно, т.к. нам известно, что существуют истинные высказывания и существуют ложные. в) 25+х≤ 7; Решение: Это предложение не является высказыванием, т.к. нельзя определить его истинность. 0Б. Постройте отрицание высказывания Q и определите его значение истинности: а) Q: «Существуют инопланетные цивилизации»;
б) Q: « Сумма внутренних углов треугольника равна 180о»; Решение: ` в) Q: «Число 21 делится на 2» Решение: .
ЛОГИКА ВЫСКАЗЫВАНИЙ (задания II уровня)
1А. Дано высказывание А: «0 – целое число». Приведите пример такого высказывания В, чтобы конъюнкция высказываний А и В была: а) истинной, б) ложной; чтобы импликация высказываний А и В была: в) истинной, г) ложной.
1Б. Выясните логическую структуру следующих высказываний и найдите их значения истинности: а) число 5 – целое или положительное; б) 16 кратно 2 и кратно 5; в) если у параллелограмма АВСD все стороны равны, то этот параллелограмм – ромб.
2А. Дано высказывание С: «Число 3 больше числа 2 на 1». Можно ли привести пример такого высказывания D, чтобы конъюнкция высказываний С и D была: а) ложной, б) истинной; чтобы импликация высказываний С и D была: в) истинной, г) ложной.
2Б. Выясните логическую структуру следующих высказываний и найдите их значения истинности: а) слово «группа» - прилагательное или глагол; б) если число 12 кратно 4, то оно кратно 2; в) число 7 – натуральное и однозначное.
3А. Дано высказывание В: «Число 7 – четное». Приведите пример такого высказывания С, чтобы дизъюнкция высказываний В и С была: а) истинной, б) ложной; чтобы импликация высказываний В и С была: в) истинной, г) ложной.
3Б. Среди следующих высказываний выделите элементарные и составные высказывания, а также укажите их значения истинности: а) число 17 не делится на 5; б) всякий равнобедренный треугольник прямоугольный и равносторонний; в) г) если число 42 делится на 2, то оно четное.
4А. Определите значения истинности высказываний А, В, D, если: а) А Ù «В слове «стол» 4 звука» ≡ И; б) «Вода в море пресная» Û В ≡ Л; в) D Þ «При 0о вода замерзает» ≡ И.
4Б. Среди следующих высказываний выделите элементарные и составные высказывания, а также укажите их значения истинности: а) число 13 простое и делится на 2; б) 122 четное число или нечетное; в) в прямоугольном треугольнике один из углов равен 90о; г) если сумма цифр числа 75 делится на 3, то число делится на 3».
5А. Определите значения истинности высказываний Е, F, G, если: а) Е Þ «Воздух хорошо проводит тепло» ≡ Л; б) «Синус любого угла меньше 1» Û F ≡ И; в) G Ú «Слово «река» – существительное» ≡ Л.
5Б. Среди следующих высказываний выделите элементарные и составные высказывания, а также укажите их значение истинности: а) слово «пальто» не склоняется; б) если арбуз – бахчевая культура, то Минск – столица Беларуси; в) гипотенуза прямоугольного треугольника, вписанного в окружность, является ее диаметром; г) все реки текут.
0А. Выясните логическую структуру следующих высказываний и найдите их значение истинности: а) «Если число 10 заканчивается цифрой 0, то оно делится на 5»; Р ешение: А Þ В – импликация высказываний, где А – условие, В – заключение. А: «Число10 заканчивается цифрой 0» – истинно; В: «Это число делится на 5» – истинно. Тогда А Þ В – истинно по определению импликации. б) «Карась – морская или речная рыба»; Решение: АÚ В – дизъюнкция высказываний А: «Карась – морская рыба» - ложно. В: «Карась – речная рыба»- истинно. Тогда АÚ В – истинно по определению дизъюнкции. в) «Число 13 четное и натуральное»; Решение: АÙ В – конъюнкция высказываний. А: «Число 13 – четное» – ложно. В: «Число 13 – натуральное» – истинно. Тогда АÙ В – ложно по определению конъюнкции.
0Б. Определите значения истинности высказываний А, В, С, если: а) «sin 90о = 0» Û А ≡ И; Решение: Дана эквиваленция 2-х высказываний, которая истинна. Известно, что эквиваленция двух высказываний истинна при одинаковых значениях истинности входящих в него высказываний. А поскольку высказывание «sin 90о = 0» – ложно, то и высказывание А – ложно. б) В Þ «тела при нагревании не расширяются» ≡ Л; Решение: Дана импликация 2-х высказываний, которая ложна. Импликация двух высказываний истинна во всех случаях, кроме одного, когда первое высказывание истинно, а второе – ложно. Высказывание «тела при нагревании не расширяются» ложно, значит, высказывание В – истинно. в) С Ù «укроп – растение семейства зонтичных» – И; Решение: Дана конъюнкция 2-х высказываний. Конъюнкция высказываний истинна тогда и только тогда, когда истинны оба высказывания. Поскольку «укроп – растение семейства зонтичных» истинное высказывание, то высказывание С – истинно.
ЛОГИКА ВЫСКАЗЫВАНИЙ (задания III уровня)
1А. Составьте таблицы истинности для высказываний: а) (АÙ В)Ù С; б)
1Б. Даны составные высказывания: а) «Множество В является подмножеством множества А тогда и только тогда, когда каждый элемент множества В является элементом множества А»; б) «Числа m и n взаимно просты тогда и только тогда, когда у них нет общих делителей». Запишите данные высказывания в виде логической формулы. Сформулируйте каждое высказывание в виде конъюнкции двух взаимно-обратных импликаций.
2А. Составьте таблицы истинности для высказываний:
2Б. Даны составные высказывания: а) «Четырехугольник АВСD является параллелограммом тогда и только тогда, когда его противоположные стороны попарно параллельны»; б) «Высказывание В является отрицанием высказываниz А тогда и только тогда, когда А и В принимают противоположные значения истинности». Запишите каждое высказывание в виде логической формулы. Сформулируйте каждое высказывание в виде конъюнкции двух взаимно-обратных импликаций.
3А. Составьте таблицы истинности для высказываний: а) СÞ (АÙ В), б) АÞ (
3Б. Даны высказывания: а) «3 и 8 – однозначные числа»; б) «Собака – домашнее или дикое животное». Запишите каждое высказывание в виде логической формулы. Сформулируйте отрицания данных высказываний двумя способами, используя законы де Моргана. Определите значения истинности данных высказываний и их отрицаний.
4А. Составьте таблицы истинности для высказываний: а) АÞ (АÙ
4Б. Даны высказывания: а) «Картофель и тыква – овощи»; б) «Число 0, 7 – натуральное или целое». Запишите каждое высказывание в виде логической формулы. Сформулируйте отрицания данных высказываний двумя способами, используя законы де Моргана. Определите значения истинности данных высказываний и их отрицаний.
5А. Составьте таблицы истинности для высказываний: а) (
5Б. Даны высказывания: а) «Число 17 – четное или делится на 5»; б) «Свекла растет в поле и в огороде». Запишите каждое высказывание в виде логической формулы. Сформулируйте отрицания данных высказываний двумя способами, используя законы де Моргана. Определите значения истинности данных высказываний и их отрицаний.
0А. Составьте таблицы истинности для высказываний:
Решение: а) АÙ В Þ
Решение:
0Б. Даны составные высказывания: а) «Треугольник является прямоугольным тогда и только тогда, когда имеет место с2=а2+в2»; б) «Число делится на 3 тогда и только тогда, когда сумма цифр в записи числа делится на 3». Запишите данные высказывания в виде логической формулы. Сформулируйте каждое высказывание в виде конъюнкции двух взаимно-обратных импликаций. Решение: а) А: «Треугольник является прямоугольным» В: «с2=а2+в2» АÛ В – данное высказывание АÛ Вº (АÞ В)Ù (ВÞ А) (АÞ В)Ù (ВÞ А): «Если треугольник прямоугольный, то с2=а2+в2 и если с2=а2+в2, то треугольник является прямоугольным». б) А: «Число делится на 3». В: «Сумма цифр в записи числа делится на 3». АÛ В º (АÞ В)Ù (ВÞ А) (АÞ В)Ù (ВÞ А): «Если число делится на 3, то сумма цифр в записи числа делится на 3, и если сумма цифр в записи числа делится на 3, то число делится на 3». ЛОГИКА ВЫСКАЗЫВАНИЙ (задания IV уровня).
1. Составьте таблицу истинности ( 2. Составьте таблицу истинности ((ХÙ 3. Составьте таблицу истинности (ХÞ (УÚ 4. Составьте таблицу истинности 5. Составьте таблицу истинности ЛОГИКА ВЫСКАЗЫВАНИЙ (задания V уровня).
1. Докажите, что следующие высказывания являются тождествами (тавтологиями): а) 2. Докажите, что следующие высказывания являются тождествами (тавтологиями): а)
3. Докажите, что следующие высказывания являются тождествами (тавтологиями): а) АÚ АÛ А; б) АÞ ВÛ
4. Докажите, что следующие высказывания являются тождествами (тавтологиями): а)
5. Докажите, что следующие высказывания являются тождествами (тавтологиями): а) (АÛ В)Û (ВÛ А); б) (АÞ В)Ú (ВÞ А).
|

 : «Не верно, что существуют инопланетные цивилизации» (ложно).
: «Не верно, что существуют инопланетные цивилизации» (ложно). =2;
=2;
 а) АÙ
а) АÙ 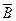 , б) АÚ ВÞ С.
, б) АÚ ВÞ С.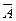 Ú В).
Ú В). ), б) АÞ (
), б) АÞ ( а) АÙ В Þ
а) АÙ В Þ  , б)
, б)  Þ (УÙ
Þ (УÙ  ))Þ ((
))Þ (( Ú Х)Þ
Ú Х)Þ 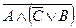


 Û
Û 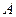 ; б)
; б)  ; в)
; в) 
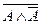 ; б) (
; б) (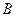 Û
Û  Þ
Þ 


