ТЕМА № 5. БИНАРНЫЕ ОТНОШЕНИЯ
Бинарные отношения между элементами одного и двух множеств. Отношения обратное и противоположное данному. Свойства бинарных отношений. Отношения эквивалентности и порядка. Литература: [1] с. 67-89; [2] с. 87-104; [3] с. 38-57; [4] с. 28-42; [5] с. 95-103; [6] с. 76-82; [7] с. 22-36.
БИНАРНЫЕ ОТНОШЕНИЯ (задания I уровня)
1А. Даны множества Х={5, 7, 8, 9, 10} и У ={3, 4, 5, 6, 9}. Между ними установлено соответствие R: «Число х на 2 больше числа у», где хÎ Х, уÎ У. Какие из следующих записей являются другими способами задания отношения R: а) Г={(3, 5), (5, 7), (6, 8), (9, 10)}; б) Г={(5, 3), (7, 5), (8, 6)}; в) R: «х=2+у», где хÎ Х, уÎ У; г) Г={(5, 3), (7, 4), (7, 5), (7, 6), (7, 3), (8, 4), (8, 3), (8, 5), (8, 6)}.
1Б. Дано множество А={2, 4, 6, 8, 10, 12}, элементы которого связаны отношением R: «Число х на 4 больше числа у», где х, уÎ А. Какие из графов соответствуют отношению R:
10 8 10• 8 • 10 8
2А. Известно, что Г – график бинарного соответствия между элементами множеств А и В, аÎ А, вÎ В. Какие из следующих предложений являются истинными при условии, что А и В – любые множества и (а, в)Î Г: а) ГÌ А; б) ГÌ В; в) ГÌ А´ В; г) (А´ В)Ç Г=Г; д) (А´ В)Ç Г= А´ В; е) (А´ В)È Г=Г; ж) (А´ В)\Г=Æ
2Б. На множестве У={у|уÎ Z, –13£ у£ –2} задано отношение R: «х=2у». Какие из следующих утверждений истинны: а) (-6, -3)Î R; б) (-3, -6)Î R; в) (-4, -2)Î R; г) (-8, -4)Ï R; д) -12R-6; е) 2R1.
3А. Даны множества А={а, е, и} и В={б, г, д, ж, з}. Между ними установлено соответствие R: «Буква х предшествует в алфавите букве у», где хÎ А, уÎ В. Какие из следующих записей являются другими способами задания соответствия R: а) Г={(а, б), (а, г), (а, д), (а, ж), (а, з), (е, б), (е, г), (е, д), (е, ж), (е, з), (и, б), (и, г), (и, д), (и, ж), (и, з)};
•г • з и• • д
в) Г={(а, б), (а, г), (а, д), (а, ж), (а, з), (е, ж), (е, з)}; г) Г={(е, б), (е, г), (е, д), (и, б), (и, г), (и, д), (и, ж), (и, з)}.
3Б. На множестве Х={х | хÎ N, х≤ 6} задано отношение Р: {(6, 6), (6, 3), (6, 2), (6, 1), (5, 5), (5, 1), (4, 4), (4, 2), (4, 1), (3, 3), (3, 1), (2, 2), (2, 1), (1, 1)}. Какие из предложений являются другими формами записи отношения Р: а) Р= {(х, у) | х, уÎ Х, х≥ у}; б) Р= {(х, у) | х, уÎ Х, х=2у}; в) Р= {(х, у) | х, уÎ Х, х – кратно у}; г) Р= {(х, у) | х, уÎ Х, х=ку, кÎ N}.
4А. Известно, что Г – график бинарного соответствия между элементами множеств А и В, аÎ А, вÎ В. Какие из следующих предложений являются истинными при условии, что А и В – любые множества и (а, в)Î Г: а) аÎ Г; б) вÎ Г; в) (а, в)Î А´ В; г) (а, в)Ì А´ В; д) {(а, в)}Ì Г; е) (в, а)Î Г; ж) {(в, а)}Ì А´ В.
4Б. На множестве Х={1, 2, 3, 4, 5, 6} задано отношение S: {(х, у) | х–у=2, х, уÎ Х}. Какие из рисунков соответствуют отношению S:
-2 х 1 -1 0 1 2 3 4 5 6 х
0 1 2 х 0 1 2 3 4 х -2
5А. Даны множества Х={1, 2, 3, 4} и У={2, 4, 6}. Между ними установлено соответствие R: «Число х не больше числа у», где хÎ Х, уÎ У. Какие высказывания являются истинными: а) Г={(1, 2), (1, 4), (1, 6), (2, 2), (2, 4), (2, 6), (3, 2), (3, 4), (3, 6), (4, 2), (4, 4), (4, 6)} – график соответствия R; б) (1, 2)Î Х´ У; в) (1, 2)Î Г; г) (2, 2) Î Г; д) (4, 6)Î Г; е) (3, 4)Î Г; ж) (3, 4)Î Х´ У.
5Б. На множестве Х={–3, –1, 1, 2, 3, 4} задано отношение R: «х=у+2». Какие, из следующих утверждений истинны: а) –1R–3; б) 1R3; в) 3R1; г) R(1)= –1; д) R(4)=2; е) R(2)= –1.
0А. Даны множества Х={1, 2, 3, 4} и В={5, 6, 7}, между которыми установлено соответствие R:
Среди предложенных записей найдите другие способы задания соответствия R: а) R={(х, у)| хÎ А, уÎ В, у–х£ 4}; б) R={(1, 5), (2, 5), (2, 6), (3, 5), (3, 6), (3, 7), (4, 5), (4, 6), (4, 7)}; в) R={(1, 5), (1, 6), (1, 7), (2, 5), (2, 6), (2, 7), (3, 5), (3, 6), (3, 7), (4, 5), (4, 6), (4, 7)} Решение: выбраны ответы а и б, т.к. графу соответствуют пары, указанные в множестве R={(1, 5), (2, 5), (2, 6), (3, 5), (3, 6), (3, 7), (4, 5), (4, 6), (4, 7)} (ответ б). Рассматривая пары этого соответствия, замечаем, что у – х £ 4, значит, соответствие R можно также задать следующим образом: R ={ (х, у)| хÎ А, уÎ В, у – х £ 4} (ответ а). 0Б. На множестве М={а, б, в, г, д} задано отношение R: «Буква х находится в алфавите непосредственно после буквы у». Какие из следующих утверждений истинны: а) Г={(б, а), (в, б), (г, в), (д, г), (а, б), (б, в), (в, г), (г, д)} – график отношения R; б) Г={(б, а), (в, б), (г, в), (д, г)} – график отношения R; в) ГÌ М2; г) R(б)=а; д) гRв. Решение: б) Г={(б, а), (в, б), (г, в), (д, г)} – график отношения R; г) R(б)=а; д) гRв; в) ГÌ М2.
БИНАРНЫЕ ОТНОШЕНИЯ (задания II уровня)
1А. На множестве А={4, 2, 6, 3, 5, -3, -8, -6, 0} заданы бинарные отношения: а) R: «а< в»; б) S: «Число а противоположно числу в», где а, вÎ А. Задайте каждое из данных отношений другими способами.
1Б. Отношение R в множестве А={а, в, с, е} задано графиком: Г={(а, в), (а, с), (в, с), (в, е), (с, е)}. Каковы область определения и множество значений отношения R? Постройте граф этого отношения. Найдите R(a), R(в), R(c), R(e), R-1(a), R-1(c).
2А. Дано множество А={2, 4, 6, 8}. Найдите декартов квадрат множества А. Запишите графики отношений: а) Р: «а> в»; б) R: «Число а – делитель числа в», а, вÎ А. Постройте графы и графики этих отношений.
2Б. Отношение Q задано при помощи таблицы. Постройте граф и график отношения Q, укажите его область определения и множество значений. Найдите: Q(4), Q(-2), Q-1(1), Q-1(2).
3А. Дано множество А={2, 3, 4, 6, 9, 10}. Найдите декартов квадрат множества А. Запишите графики отношений: а) Q: «Число а делится на число в», а, вÎ А. б) Т: «Число а не больше, чем число в», а, вÎ А. Постройте графы и графики данных отношений. 3Б. Отношение S в множестве Х={-2, -1, 0, 1, 2, 3} задано графиком Г={(-2, 0), (-1, 1), (0, 2), (1, 3)}. Каковы область определения и множество значений отношения S? Постройте граф и график этого отношения. Найдите S(1), S(0), S(-1), S-1(2), S-1(3).
4А. Элементы множеств Х и У находятся в отношении у=х–3. постройте график данного отношения, если: а) Х=У=R; б) Х=[-2, 2], У=R; в) Х={-2, -1, 0, 1, 2}, У=Z.
4Б. На рисунке изображен график отношения Е, заданного на множестве R. Каковы область определения и множество значений отношения Е? Постройте график отношения Е-1.
-2 0 1 х
5А. Постройте график отношения у> 3х–2, заданного на множестве Х, если: а) Х=R; б) Х=Z.
5Б. На рисунке изображен график отношения S, заданного на множестве R. Найдите область определения и множество значений отношения S? Найдите S-1(1), S-1(2).
-2
0А. На множестве А={х|хÎ N, х≤ 6} заданы бинарные отношения: а) R: «Число а вдвое больше числа в»; б) Q: «Число а делится на в», где а, вÎ А. Задайте каждое из данных отношений другими способами. Решение: А={1, 2, 3, 4, 5, 6} а) 1 способ: R ={(2, 1), (4, 2), (6, 3)}; R ={(х, у)| х, уÎ А; х=2у}. 2 – графический. 3 – с помощью графа:
R
4 – в виде таблицы:
б) 1 способ: Q={(1, 1), (2, 1), (3, 1), (4, 1), (5, 1), (6, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6), (4, 2), (6, 2), (6, 3)} Q={(х, у)| х, уÎ А; х = у× к; кÎ N}. 2 способ: графический 3 способ: с помощью графа:
0Б. Отношение задано таблицей:
Постройте граф и график отношения R, укажите его область определениях и множество значений у. Найдите R(0), R(1), R-1(1), R-1(2). Решение: график отношения R график отношения R
R(0) ={1, - 1, 2}, R(1) ={-1, 1, 2}, R-1(1) ={0, 1, 2}, R-1(2) ={0, 1} Область определения Х ={0, 1, 2} Множество значений У={-1, 1, 2}
БИНАРНЫЕ ОТНОШЕНИЯ (задания III уровня)
1А. На множестве Х={2, 3, 4, 6, 8, 9} задано отношение R: «Число х кратно числу у», где х, уÎ Х. Постройте граф и график отношений R. Сформулируйте обратное и противоположное отношения, постройте их граф и график.
1Б. На множестве Х={а, в, с, d} заданы графики отношений Р={(а, а), (а, в), (а, с), (с, с), (d, d)}; R={(в, а), (а, в), (в, с), (с, в), (в, d), (d, в), (с, d), (d, с)}; S={(а, а), (в, в), (с, с), (d, d), (в, с), (с, в), (с, d), (d, с)}. Какие из данных отношений являются: а) рефлексивными; б) симметричными; в) транзитивными.
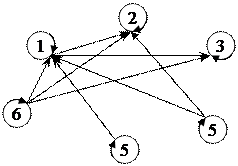
2А. Бинарное отношение R задано на множестве {1, 2, 3, 4, 5, 6} графом, показаным на рисунке. Задайте это отношение характеристическим свойством. Запишите график отношения R. Назовите его область определения и множество значений. Постройте графы отношений, обратного и противоположного отношению R. Укажите характеристические свойства отношений R-1 и
5 6
2Б. На множестве прямых плоскости задано отношение S перпендикулярности прямых. Обладает ли это отношение свойством рефлексивности, свойством транзитивности? Ответ обоснуйте.
3А. На множестве Х={1, 2, 3, 4, 5, 6} задано отношение R: «Число х меньше числа у», где х, уÎ Х. Постройте граф и график отношения R. Сформулируйте и постройте граф и график обратного и противоположного отношений.
3Б. На множестве Х={2, 4, 6, 8} задано отношение R: «х≤ у», х, уÎ Х. Запишите график отношения R. Постройте его граф. Обладает ли отношение R свойством рефлексивности, симметричности, транзитивности? Как это выражается на графе?
4А. На рисунке показан график отношения Т, заданного на множестве {-3, -2, -1, 1, 2}. Запишите множество элементов, принадлежащих отношению Т. Укажите его характеристическое свойство. Постройте граф отношения Т. Назовите характеристические свойства отношений
• •1 • •
4Б. Известно, что отношение К, заданное на множестве Х={3, 4, 5}, рефлексивно и транзитивно. Какое из следующих множеств задает отношение К: а) {(3, 3), (3, 4), (4, 3), (4, 4), (5, 5)}; б) {(3, 3), (4, 4), (5, 5), (3, 4), (4, 5), (5, 4)}. Объясните, почему.
5А. На множестве Х={1, 2, 3, 4, 5, 6} задано отношение S: «Число х предшествует числу у в натуральном ряду», х, уÎ Х. Постройте граф и график отношений R. Сформируйте и постройте граф и график обратного и противоположного отношений. 5Б. На множестве Х={0, 1, 2, 3} задано отношение S={(0, 0), (1, 1), (2, 2), (3, 3), (0, 1), (1, 2), (0, 2), (1, 0), (2, 1), (2, 0)}. Определите свойства отношения S и постройте его график. Как отражаются свойства отношения на его графике? 0А. На множестве Х={х|хÎ N, х≤ 4} задано отношение S: «Число х меньше числа у», х, уÎ Х. Постройте граф и график отношений S. Сформулируйте обратное и противоположное отношения и постройте их граф и график. Решение: Х={1, 2, 3, 4}. S={(1, 2), (1, 3), (1, 4), (2, 3), (2, 4), (3, 4)} S-1: «Число у больше числа х» - обратное соответствие
S-1={(2, 1), (3, 1), (4, 1), (3, 2), (4, 2), (4, 3)}
0Б. На множестве Х={1, 3, 5, 7, 9} задано отношение R: «Число х больше числа у на 2», где х, уÎ Х. Запишите график отношения R. Постройте его график и граф. Обладает ли отношение R свойствами рефлексивности, симметричности? Как это определить по графу? По графику?
Отношение R не обладает свойством рефлексивности. Т.к. любой элемент из множества Х, не находится в отношении R с самим собой, а именно: не существует числа, которое было бы на 2 больше самого себя. На графе нет петель. График отношения R не лежит на биссектрисе 1 и 3 координатных углов. Отношение R, заданное на множестве Х, не обладает свойством симметричности, т.к. для любого элемента из множества Х из того, что х находится в отношении R с у не следует, что у находится в отношении R с х (хRу Þ уRх) – «л.» Т.е. если число у больше числа х на 2, то не верно, что число у больше числа х на 2. На графе стрелки между любыми двумя элементами идут болько в одном направлении. График отношения R не симметричен относительно биссектрисы 1 и 3 координатных углов.
БИНАРНЫЕ ОТНОШЕНИЯ (задания IV уровня)
1А. Выясните, какими свойствами обладают данные отношения. Назовите среди них отношения эквивалентности и отношения порядка: а) «а равно в» (в множестве треугольников); б) «а меньше или равно в» (в множестве Z); в) «а является собственным подмножеством в» (в множестве геометрических фигур).
1Б. В множестве учащихся класса выделены подмножества отличников, спортсменов и мальчиков. Можно ли сказать, что множество учащихся разбито на эти три подмножества? Почему?
2А. Выясните, какими свойствами обладают данные отношения. Назовите среди них отношения эквивалентности и отношения порядка: а) «а концентрично в» (в множестве окружностей на плоскости); б) «а следует за в» (в множестве N); в) «а является дополнением в до прямоугольника» (в множестве геометрических фигур).
2Б. На плоскости проведена прямая l. Можно ли сказать, что множество всех прямых плоскости разбивается на три класса: параллельные l, перпендикулярные l и пересекающие l? Почему?
3А. Выясните, какими свойствами обладают данные отношения. Назовите среди них отношения эквивалентности и отношения порядка: а) «а равно в» (в множестве Q); б) «а является подмножеством в» (в множестве геометрических фигур); в) «а кратно в» (в множестве N).
3Б. Можно ли разбить множество треугольников на равнобедренные, разносторонние, равносторонние? Ответ обоснуйте.
4А. На множестве людей заданы отношения: а) «а сестра в»; б) «а имеет тот же цвет глаз, что и в»; в) «а на 4 см выше, чем в». Выясните свойства этих отношений. Назовите отношения эквивалентности и порядка.
4Б. На плоскости проведена окружность. Можно ли разбить множество всех окружностей на два класса: касающихся данной окружности и пересекающихся с ней. Завершите классификацию окружностей.
5А. На множестве людей заданы отношения: а) «а начальник в»; б) «а друг в»; в) «а родился в том же году, что и в». Выясните свойства отношений. Назовите отношения эквивалентности и порядка.
5Б. Можно ли разбить множество целых чисел на четные и нечетные? Ответ обоснуйте. БИНАРНЫЕ ОТНОШЕНИЯ (задания V уровня)
1А. Выясните свойства следующих отношений в множестве Z: а) (х–у)M3; б) х2=у2; в) |х|< |у|.
1Б. На рисунке с плотными стрелками обозначен граф отношения «а брат в», штриховыми – граф отношения «а сестра в». некоторые стрелки пропущены. Восстановите их. Кто из детей мальчик, кто – девочка?
В Е К
2А. Выясните свойства следующих отношений в множестве Z: а) х: у=4; б) |х|+|у|= 3; в) х3=у3.
2Б. На рисунке изображен граф отношения «а дед в». Кем приходились друг другу отец и мать d?
3А. Выясните свойства следующих отношений в множестве Z: а) |х|+|у|≠ 4; б) х≠ у; в) (х2–у2) M4.
3Б. На рисунке изображен граф отношения «больше, чем» в множестве числовых выражений. Подберите выражения, которые можно поставить в прямоугольники. Проиллюстрируйте, что отношение «больше, чем» транзитивно.
4А. Какие из отношений в множестве Х являются отношениями эквивалентности? Для отношений эквивалентности укажите классы эквивалентности: а) Х=Z, (х-у) M3; б) Х=N, (х+у) M2; в) Х=Z, х2=у2.
4Б. Даны графы отношения «меньше, чем». Какое из чисел А, В, С, Д самое большое? Какое самое маленькое? Придайте А, В, С и Д подходящие значения.
С С
5А. Какие из отношений в множестве Х являются отношениями эквивалентности? Для отношений эквивалентности укажите классы эквивалентности: а) Х=N, (х-у) M3; б) Х= Nо, (х–у) M3 или (у–х) M3; в) Х=R, х–у=2.
5Б. Дан граф отношения «больше, чем». Точками изображены все элементы рассматриваемого множества, но один элемент t – неизвестен. Определите t, если: а) tÎ N, б) tÎ R.
2 t
ЛИТЕРАТУРА
1. Виленкин Н. Я. Математика / Н. Я. Виленкин, А. М. Пышкало, В. Б. Рождественская [и др.] – М.: Просвещение, 1977. – 352 с. 2. Задачник-практикум по математике. / Н. Я. Виленкин, Н. Н. Лав-рова [и др.]; под ред. Н. Я. Виленкина. – М.: Просвещение, 1977. – 205 с. 3. Кожух І. Р. Матэматыка / І. Р. Кожух. – Мінск: Вышэйшая школа, 1993. – 350 с. 4. Кожух І. Р. Зборнік задач па матэматыцы: вучэб. дапам. для пед. ВНУ / І. Р. Кожух. – Мінск: Вышэйшая школа, 1994. – 162 с. 5. Лаврова Н. Н. Задачник-практикум по математике / Н. Н. Лаврова, Л. П. Стойлова. – М.: Просвещение, 1985. – 180 с. 6. Сендер А. Н. Методология формирования понятия о числе в начальном курсе математики / А. Н. Сендер. – Брест: БрГУ, 2003. – 164 с. 7. Стойлова Л. П. Математика: В 2 ч. / Л. П. Стойлова, Н. Я. Вилен-кин, Н. Н. Лаврова. – М.: Просвещение, 1990. Ч. 1. – 173 с.
Онискевич Татьяна Сергеевна
|











 а)2 4 б) 2 4 в) 2 4 г)2
а)2 4 б) 2 4 в) 2 4 г)2

 12 6 12 4
12 6 12 4






 12 6 6 6
12 6 6 6 10 8 12
10 8 12 б) А R В
б) А R В





 а• • ж
а• • ж е• • б
е• • б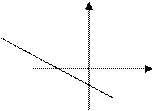
 а) у б) у
а) у б) у у
у в) у г)
в) у г)
 у
у 3
3
 у
у
 3
3 -1 0 1 х
-1 0 1 х



 .
.
 1
1
 2 4
2 4 и Т -1, запишите их графики.
и Т -1, запишите их графики. у
у
 • 3
• 3


 -3 -2 -1 0 1 2 3 х
-3 -2 -1 0 1 2 3 х • • •
• • • • -2
• -2



 : «Число х больше либо равно числа у» - противоположное соответствие.
: «Число х больше либо равно числа у» - противоположное соответствие.

 Решение: Г={(3, 1), (5, 3), (7, 5), (9, 7)} – график отношения R.
Решение: Г={(3, 1), (5, 3), (7, 5), (9, 7)} – график отношения R.



 А Б Г Д З
А Б Г Д З




 Ж И
Ж И
 в
в а d
а d с
с

 а) б)
а) б)










 8 5
8 5



